使用 scikit-learn 构建模型

1. sklearn 介绍

  scikit-learn（简称 sklearn）是一个简单有效的数据挖掘和数据分析工具，可以提供用户在各种环境下重复使用。而且 sklearn 建立在 Numpy、Scipy 和 Matplotlib 基础之上，对一些常用的算法进行了封装。目前，sklearn 的基本模块主要有 数据预处理、模型选择、分类、聚合、数据降维 和 回归 6 个。
  在数据量不大的情况下，sklearn 可以解决大部分问题。sklearn 库整合了多种机器学习算法，可以帮助使用者在数据分析过程中快速建立模型，且模型接口统一，使用起来非常方便。对于算法不精通的用户在执行建模任务时，并不需要自行编写所有的算法，只需简单地调用 sklearn 库里的模块就可以。

scikit-learn 0.22.1 官方文档

2. sklearn 转换器处理数据

  sklearn 提供了 model_selection 模型选择模块、preprocessing 数据预处理模块与 decomposition 特征分解模块。通过这三个模块能够实现数据预处理与模型构建前的数据标准化、二值化、数据集分割、交叉验证和 PCA 降维等工作。

2.1 加载数据集

  sklearn 库的 datasets 模块集成了部分数据分析的经典数据集，可以使用这些数据集进行数据预处理、建模等操作，熟悉 sklearn 的数据分析流程和建模流程。使用 sklearn 进行数据预处理会用到 sklearn 提供的统一接口——转换器（Transformer）。

datasets 模块常用数据集加载函数

数据集加载函数	类型	说明	数据集加载函数	类型	说明
load_boston	回归	波士顿房价数据集	load_diabetes	回归	糖尿病数据集
load_breast_cancer	分类	乳腺癌数据集	load_iris	分类	鸢尾花数据集
load_wine	分类	葡萄酒数据集	load_digits	分类	数字数据集

# 加载breast_cancer数据集
from sklearn.datasets import load_breast_cancer

cancer = load_breast_cancer()         # 加载后的数据集可以视为一个字典
print('breast_cancer数据集的key为：\n',cancer.keys())
print('breast_cancer数据集的长度为：',len(cancer))
print('breast_cancer数据集的类型为：',type(cancer))

# 数据集内部信息获取
cancer_data = cancer['data']
print('breast_cancer数据集的数据为：\n',cancer_data)

cancer_target = cancer['target']
print('breast_cancer数据集的标签为：\n',cancer_target)

cancer_target_names = cancer['target_names']
print('breast_cancer数据集的标签名为为：\n',cancer_target_names)

cancer_names = cancer['feature_names']
print('breast_cancer数据集的特征名为：\n',cancer_names)

cancer_filename = cancer['filename']
print('breast_cancer数据集的文件名为：\n',cancer_filename)

cancer_desc = cancer['DESCR']
print('breast_cancer数据集的描述信息为：\n',cancer_desc)

注：数据集的描述性信息比较多，这里只展示部分结果。

2.2 划分数据集

  在数据分析过程中，为了保证模型在实际系统中能够起到预期作用，一般需要将样本分成独立的三部分：训练集（train set）、验证集（validation set）和 测试集（test set）。其中，训练集用于估计模型，验证集用于确定网络结构或者控制模型复杂程度的参数，而测试集则用于检验最优模型的性能。典型的划分方式是训练集占总样本的 50%，而验证集和测试集各占 25%。
  当数据较少的时候，使用上面的方法将数据分为 3 部分就不合适了。常用的方法是留少部分数据做测试集，然后对其余 $N$ 个样本采用 $K$ 折交叉验证法。其基本步骤是将样本打乱，然后均匀分成 $K$ 份，轮流选择其中 $(K-1)$ 份做训练，剩余一份做验证，计算预测误差平方和，最后把 $K$ 次的预测误差平方和的均值作为选择最优模型结构的依据。
  sklearn 的 model_selection 模块提供了 train_test_split 函数，能够对数据集进行拆分。

sklearn.model_selection.train_test_split(*arrays, **options)

train_test_split 函数官方文档

train_test_split 函数常用参数说明

参数名称	说明
*arrays	接收一个或多个数据集。代表要划分的数据集。若为分类回归，则分别传入数据和标签；若为聚类，则传入数据。无默认。
test_size	接收 float、int 类型数据或者 None。代表测试集大小。若传入的为 float 类型的数据，则需要想定 0~1 之间，代表测试集在总数中的占比；若传入的为 int 类型的数据，则表示测试集记录的绝对数目。该参数与 trian_size 可以只传入一个。若 test_size 和 train_size 均为默认，则 test_size 为 25%。
train_size	接收 float、int 类型数据或者 None。代表训练集大小。
random_state	接收 int。代表随机种子编号。相同随机种子编号产生相同的随机结果。默认为 None。

# 使用train_test_split划分数据集
from sklearn.model_selection import train_test_split

cancer_data_train, cancer_data_test, cancer_target_train, cancer_target_test = \
train_test_split(cancer_data,cancer_target,test_size=0.2,random_state=42)

print('原始数据集的形状为：',cancer_data.shape)
print('原始数据集标签的形状为：',cancer_target.shape)
print('训练集数据的形状为：',cancer_data_train.shape)
print('训练集标签的形状为：',cancer_target_train.shape)
print('测试集数据的形状为：',cancer_data_test.shape)
print('测试集标签的形状为：',cancer_target_test.shape)

2.3 数据预处理与降维

  为帮助用户实现大量的特征处理相关操作，sklearn 把相关的功能封装为转换器。转换器主要包括三个方法：fit、transform 和 fit_transform。

转换器的 3 个方法说明

方法名称	说明
fit	fit 方法主要通过分析特征和目标值提取有价值的信息，这些信息可以是统计量，也可以是权值系数。
transform	transform 方法主要用来对特征进行转换。从可利用信息的角度分为无信息转换和有信息转换。无信息转换是指不利用任何其他信息进行转换，比如指数和对数函数进行转换等。有信息转换根据是否利用目标值向量又可分为无监督转换和有监督转换。无监督转换只利用特征的统计信息的转换，比如标准化和 PCA 降维等。有监督转换指既利用了特征信息又利用了目标值信息的转换，比如通过模型选择特征和 LDA 降维。
fit_transform	fit_transform 方法就是先调用 fit 方法，然后调用 transform 方法。

  目前，使用 sklearn 转换器能够实现对传入的 Numpy 数组进行标准化处理、归一化处理、二值化处理和 PCA 降维等操作。
  在我的上一篇博客中，基于 pandas 库介绍了标准化原理、概念与方法。但是在数据分析过程中，各类特征处理相关的操作都需要对训练集和测试集分开进行，需要将训练集的操作规则、权重系数等应用到测试集中。如果使用 pandas，则应用至测试集的过程相对繁琐。使用 sklearn 转换器可以解决这一困扰。

sklearn 中 prepocessing 模块常用预处理函数说明

函数名称	说明	函数名称	说明
MinMaxScaler	对特征进行离差标准化	StandardScaler	对特征进行标准差标准化
Normalizer	对特征进行归一化	Binarizer	对定量特征进行二值化处理
OneHotEncoder	对定性特征进行独热编码处理	FunctionTransformer	对特征进行自定义函数变换

# 离差标准化
import numpy as np
from sklearn.preprocessing import MinMaxScaler

Scaler = MinMaxScaler().fit(cancer_data_train)            # 生成规则
cancer_trainScaler = Scaler.transform(cancer_data_train)  # 将规则应用到训练集
cancer_testScaler = Scaler.transform(cancer_data_test)    # 将规则应用到测试集

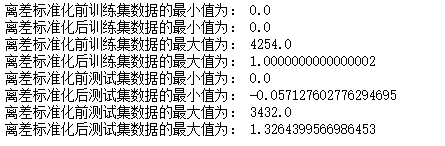
print('离差标准化前训练集数据的最小值为：',np.min(cancer_data_train))
print('离差标准化后训练集数据的最小值为：',np.min(cancer_trainScaler))
print('离差标准化前训练集数据的最大值为：',np.max(cancer_data_train))
print('离差标准化后训练集数据的最大值为：',np.max(cancer_trainScaler))

print('离差标准化前测试集数据的最小值为：',np.min(cancer_data_test))
print('离差标准化后测试集数据的最小值为：',np.min(cancer_testScaler))
print('离差标准化前测试集数据的最大值为：',np.max(cancer_data_test))
print('离差标准化后测试集数据的最大值为：',np.max(cancer_testScaler))

  sklearn 除了提供基本的特征变换函数外，还提供了降维算法、特征选择算法，这些算法的使用也是通过转换器的方式进行的。
  sklearn 的 decomposition 模块提供 PCA 降维方法。PCA（Principal Component Analysis，主成分分析）

sklearn.decomposition.PCA(n_components=None, copy=True, whiten=False, svd_solver='auto', tol=0.0, 
					iterated_power='auto', random_state=None)

PCA 函数官方文档

PCA 降维算法常用参数说明

参数名称	说明
n_components	接收 None、int、float 或 ‘mle’。未指定时，代表所有特征均会被保留下来；如果为 int，则表示将原始数据降低到 n 个维度；如果为 float，则 PCA 根据样本特征方差来决定降维后的维度数；赋值为 “mle”，PCA 会用 MLE 算法根据特征的方差分布情况自动选择一定数量的主成分特征来降维。默认为 None。
copy	接收 boolean。代表是否在运行算法时将原始数据复制一份，若为 True，则运行后，原始数据的值不会有任何改变；若为 False，则运行 PCA 算法后，原始数据的值会发生改变。默认为 True。
whiten	接收 boolean。表示白化，就是对降维后的数据的每个特征进行归一化，让方差都为 1。默认为 False。
svd_solver	接收 auto、full、arpack、randomized。代表使用的 SVD 算法。randomized 一般适用于数据量大，数据维数多，同时主成分数目比例又较低的 PCA 降维，它使用了一些加快 SVD 的随机算法。full 是使用 Scipy 库实现的传统 SVD 算法。arpack 和 randomized 的适用场景类似，区别是，randomized 使用的是 sklearn 自己的 SVD 实现，而 arpack 直接使用了 Scipy 库的 sparse SVD 实现。 auto 则代表 PCA 类会自动在上述 3 种算法中权衡，选择一个合适的 SVD 算法来降维。默认为 auto。

# 对breast_cancer数据集进行PCA降维
from sklearn.decomposition import PCA

pca_model = PCA(n_components=10).fit(cancer_trainScaler)   # 生成规则
cancer_trainPca = pca_model.transform(cancer_trainScaler)  # 将规则应用到训练集
cancer_testPca = pca_model.transform(cancer_testScaler)    # 将规则应用到测试集

print('PCA降维前训练集数据的形状为：',cancer_trainScaler.shape)
print('PCA降维后训练集数据的形状为：',cancer_trainPca.shape)
print('PCA降维前测试集数据的形状为：',cancer_testScaler.shape)
print('PCA降维后测试集数据的形状为：',cancer_testPca.shape)

3. 聚类模型

  聚类分析是在没有给定划分类别的情况下，根据数据相似度进行样本分组的一种方法。聚类模型可以将无类标记的数据聚集为多个簇，视为一类，是一种无监督的学习算法。在商业上，聚类可以帮助市场分析人员从消费者数据库中区分出不同的消费群体，并且概括出每一类消费者的消费模式或消费习惯。同时，聚类分析也可以作为数据分析算法中其他分析算法的一个预处理步骤，如异常值识别、连续型特征离散化等。

3.1 构建聚类模型

  聚类的输入是一组未被标记的样本，聚类根据数据自身的距离或相似度将它们划分为若干组，划分的原则是组内（内部）距离最小化，而组间（外部）距离最大化。

聚类算法类别

算法类别	主要算法
划分（分裂）方法	K-Means 算法（K-平均）、K-MEDOIDS 算法（K-中心点）和 CLARANS（基于选择的算法）
层次分析方法	BIRCH 算法（平衡迭代规约和聚类）、CURE 算法（代表点聚类）和CHAMELEON 算法（动态模型）
基于密度的方法	DBSCAN 算法（基于高密度连接区域）、DENCLUE 算法（密度分布函数）和 OPTICS 算法（对象排序识别）
基于网格的方法	STING 算法（统计信息网格）、CLIOUE 算法（聚类高维空间）和 WAVE-CLUSTER 算法（小波变换）

sklearn 的 cluster 模块提供的聚类算法说明

函数名称	主要参数	适用范围	距离度量
KMeans	簇数	可用于样本数目很大，聚类数目中等的场景	点之间距离
SpectralClustering	簇数	可用于样本数目中等、聚类数目较少的场景	图距离
AgglomerativeClustering	簇数、链接类型、距离	可用于样本数目较大、聚类数目较大的场景	任意成对点线图间的距离
DBSCAN	半径大小、最低成员数目	可用于样本数目很大，聚类数目中等的场景	最近的点之间的距离
Birch	分支因子、阈值可选全局集群	可用于样本数目很大，聚类数目较大的场景	点之间的欧式距离

KMeans 函数官方文档

  聚类算法实现需要 sklearn 估计器（Estimator）。sklearn 估计器拥有 fit 和 predict 两个方法。

估计器两个方法说明

方法名称	说明
fit	fit 方法主要用于训练算法。该方法可接受用于有监督学习的训练集即标签两个参数，也可以接受用于无监督学习的数据。
predict	predict 用于预测有监督学习的测试集标签，亦可以用于划分传入数据的类别。

# 使用sklearn估计器构建K-Means聚类模型
from sklearn.datasets import load_iris
from sklearn.preprocessing import MinMaxScaler
from sklearn.cluster import KMeans

iris = load_iris()
iris_data = iris['data']
iris_target = iris['target']
iris_names = iris['feature_names']

scaler = MinMaxScaler().fit(iris_data)         # 训练规则
iris_dataScaler = scaler.transform(iris_data)  # 应用规则

kmeans = KMeans(n_clusters=3, random_state=123).fit(iris_dataScaler) # 构建并训练模型

print('构建的K-Means模型为：\n',kmeans)
result = kmeans.predict([[1.5,1.5,1.5,1.5]])
print('花瓣花萼长度宽度都为1.5的鸢尾花预测类别为：',result)

  聚类完成后需要通过可视化的方式查看聚类效果，通过 sklearn 的 manifold 模块中的 TSNE 函数可以实现多维数据的可视化展现。

TNSE 函数官方文档

# 聚类结果可视化
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.manifold import TSNE 

# 使用TSNE将数据降维，降成两维
tsne = TSNE(n_components=2,init='random',random_state=177).fit(iris_data)

df = pd.DataFrame(tsne.embedding_) # 将原始数据转换为DataFrame
df['labels'] = kmeans.labels_      # 将聚类结果存储进df中

# 提取不同标签的数据
df1 = df[df['labels']==0]
df2 = df[df['labels']==1]
df3 = df[df['labels']==2]

# 绘制图形
plt.plot(df1[0],df1[1],'bo',df2[0],df2[1],'r*',df3[0],df3[1],'gD')
plt.show()

3.2 评价聚类模型

  聚类评价的标准是组内的对象之间是相似的（相关的），而不同组中的对象是不同的（不相关的）。即组内的相似性越大，组间差别越大，聚类效果就越好。
  sklearn 的 metrics 模块提供的聚类模型评价指标如下。

metrics 模块提供的聚类模型评价指标

sklearn 函数	方法名称	真实值	最佳值	官方文档链接
adjusted_rand_score	ARI 评价法（兰德系数）	需要	1.0	官方文档
adjusted_mutual_info_score	AMI 评价法（互信息）	需要	1.0	官方文档
v_measure_score	V-measure 评分	需要	1.0	官方文档
fowlkes_mallows_score	FMI 评分	需要	1.0	官方文档
silhouette_score	轮廓系数评价法	不需要	畸变程度最大	官方文档
calinski_harabaz_score	Calinski-Harabaz 指数评价法	不需要	相较最大	官方文档

  其中前 4 种方法均需要真实值的配合才能够评价聚类算法的优劣，后两种则不需要真实值的配合。但是前 4 种方法评价的效果更具有说服力，并且在实际运行的过程中，在真实值做参考的情况下，聚类方法的评价可以等同于分类算法的评价。
  除了轮廓系数评价法以外的评价算法，在不考虑业务场景的情况下都是得分越高，其效果越好，最高分值为 1。而轮廓系数评价法则需要判断不同类别数目情况下的轮廓系数的走势，寻找最优的聚类数目。

# (一)使用FMI评价方法评价K-Means聚类模型
from sklearn.metrics import fowlkes_mallows_score

for i in range(2,7):
    kmeans = KMeans(n_clusters=i,random_state=123).fit(iris_data)
    score = fowlkes_mallows_score(iris_target,kmeans.labels_)
    print('iris数据集聚%d类FMI评价分值为：%f'%(i,score))

    
# (二)使用轮廓系数评价法评价K-Means聚类模型
from sklearn.metrics import silhouette_score
import matplotlib.pyplot as plt

silhouetteScore = []
for i in range(2,15):
    kmeans = KMeans(n_clusters=i,random_state=123).fit(iris_data)
    score = silhouette_score(iris_data,kmeans.labels_)
    silhouetteScore.append(score)

plt.plot(range(2,15),silhouetteScore)
plt.show()


# (三)使用Calinski-Harabasz指数评价K-Means聚类模型
from sklearn.metrics import calinski_harabasz_score

for i in range(2,7):
    kmeans = KMeans(n_clusters=i,random_state=123).fit(iris_data)
    score = calinski_harabasz_score(iris.data,kmeans.labels_)
    print('iris数据集聚%d类calinski_harabasz指数为：%f'%(i,score))

  使用 FMI 评价法时，iris 数据 3 类的时候 FMI 评价法分值最高，故聚类为 3 类的时候 K-Means聚类模型最好。使用轮廓系数评价法时，做出轮廓系数走势图，根据图形判断聚类效果。可以看出，聚类数目为 2、3 和 5、6 时平均畸变程度最大。由于 iris 数据本身就是 3 种鸢尾花花瓣、花萼长度和宽度的数据，侧面说明了聚类数目为 3 效果最佳。使用 Calinski-Harabaz 指数评价法时，聚类数目为 3 时得分最高，所以聚类为 3 类的时候 K-Means聚类模型最好。

4. 分类模型

  分类是指构造一个分类模型。输入样本的特征值，输出对应的类别，将每个样本映射到预先定义好的类别。分类模型建立在已有类标记的数据集上，属于监督学习。在实际应用场景中，分类算法被用于行为分析、物品识别、图像检测等。

4.1 构建分类模型

  在数据分析领域，分类的算法很多，其原理千差万别，有基于样本距离的最近邻算法，有基于特征信息熵的决策树，有基于 bagging 的随机森林，有基于 boosting 的梯度提升分类树，但其实现的过程相差不大。sklearn 中提供的分类算法风非常多，分别存在于不同的模块中。常见的分类算法如下表。

sklearn 库的常用分类算法

模块名称	函数名称	算法名称	官方文档链接
linear_model	LogisticRegression	逻辑斯蒂回归	官方文档
svm	SVC	支持向量机	官方文档
neighbors	KNeighborsClassifier	K 最邻近分类	官方文档
native_bayes	GaussianNB	高斯朴素贝叶斯	官方文档
tree	DessionTreeClassifier	分类决策树	官方文档
ensemble	RandomForestClassifier	随机森林分类	官方文档
ensemble	GradientBoostingClassifier	梯度提升分类树	官方文档

# 使用sklearn估计器构建SVM模型
import numpy as np
from sklearn.datasets import load_breast_cancer
from sklearn.svm import SVC
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler

cancer = load_breast_cancer()
cancer_data = cancer['data']
cancer_target = cancer['target']
cancer_names = cancer['feature_names']

# 划分数据集
cancer_data_train, cancer_data_test, cancer_target_train, cancer_target_test = \
train_test_split(cancer_data,cancer_target,test_size=0.2,random_state=42)

# 数据标准化
stdScaler = StandardScaler().fit(cancer_data_train)
cancer_trainStd = stdScaler.transform(cancer_data_train)
cancer_testStd = stdScaler.transform(cancer_data_test)

# 建立SVM模型
svm = SVC().fit(cancer_trainStd,cancer_target_train)
print('建立的SVM模型为：\n',svm)

# 预测训练集结果
cancer_target_pred = svm.predict(cancer_testStd)
print('预测前20个结果为：\n',cancer_target_pred[:20])

# 计算准确率
true = np.sum(cancer_target_pred == cancer_target_test)
print('预测对的结果数目为：',true)
print('预测错的结果数目为：',cancer_target_pred.shape[0]-true)
print('SVM模型预测结果的准确率为：',true/cancer_target_pred.shape[0])

4.2 评价分类模型

  分类模型对测试集进行预测而得出的准确率并不能很好地反映模型的性能，为了有效判断一个预测模型的性能表现，需要结合真实值计算出准确率、召回率、F1 值和 Cohen’s Kappa 系数等指标来衡量。
  sklearn 的 metrics 模块提供的分类模型评价指标如下。

metrics 模块提供的分类模型评价指标

sklearn 函数	方法名称	最佳值	官方文档链接
accuracy_score	准确率	1.0	官方文档
precision_score	Precision（精确率）	1.0	官方文档
recall_score	Recall（召回率）	1.0	官方文档
f1_score	F1 值	1.0	官方文档
cohen_kappa_score	Cohen’s Kappa 系数	1.0	官方文档
roc_curve	ROC 曲线	最靠近 y 轴	官方文档

# 分类模型常用评价方法
from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score, cohen_kappa_score

print('使用SVM模型预测breast_cancer数据的准确率为：',
     accuracy_score(cancer_target_test,cancer_target_pred))
print('使用SVM模型预测breast_cancer数据的精确为：',
     precision_score(cancer_target_test,cancer_target_pred))
print('使用SVM模型预测breast_cancer数据的召回率为：',
     recall_score(cancer_target_test,cancer_target_pred))
print('使用SVM模型预测breast_cancer数据F1值为：',
     f1_score(cancer_target_test,cancer_target_pred))
print('使用SVM模型预测breast_cancer数据的Cohen\'s kappa 系数为：',
     cohen_kappa_score(cancer_target_test,cancer_target_pred))


# 分类模型评价报告
from sklearn.metrics import classification_report

print('使用SVM预测breast_cancer数据的分类报告为：\n',
     classification_report(cancer_target_test,cancer_target_pred))


# 绘制ROC曲线
from sklearn.metrics import roc_curve
import matplotlib.pyplot as plt

fpr,tpr,thresholds = roc_curve(cancer_target_test,cancer_target_pred)

plt.figure(figsize=(10,6))
plt.xlim(0,1)
plt.ylim(0.0,1.1)
plt.xlabel('False Postive Rate')
plt.ylabel('True Postive Rate')
plt.plot(fpr,tpr)
plt.show()

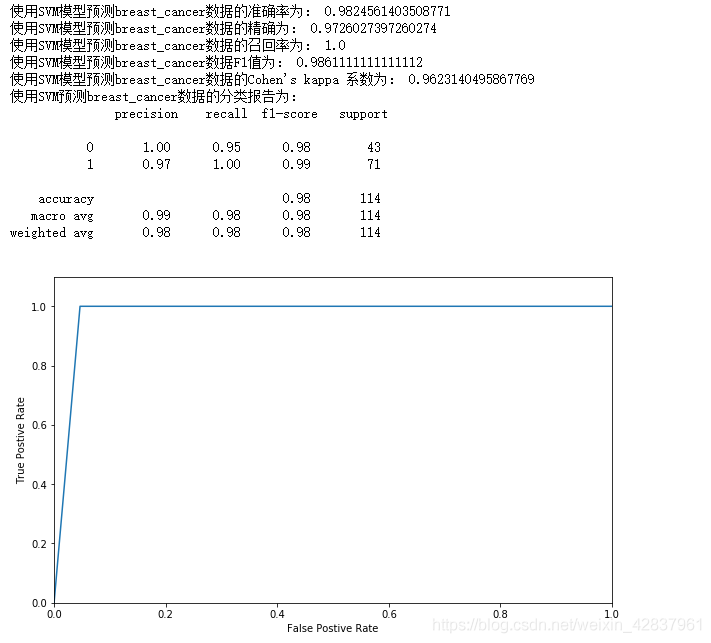
  ROC 曲线纵坐标范围为 [0,1]，通常情况下，ROC 曲线与 x 轴形成的面积越大，表示模型的性能越好。

5. 回归模型

  回归算法的实现过程与分类算法类似，原理相差不大。分类和回归的主要区别在于，分类算法的标签是离散的，但是回归算法标签是连续的。

5.1 构建回归模型

  从 19 世纪高斯提出最小二乘法起，回归分析的历史已有 200 多年。从经典的回归分析方法到近代的回归分析方法，按照研究方法划分，回归分析研究的范围大致如下所示。

$$回归分析\{\begin{array}{l}线性回归\{\begin{array}{l}一元线性回归\\ 多元线性回归\\ 多个因变量与多个自变量的回归\end{array}\\ 回归诊断\{\begin{array}{l}如何从数据推断回归模型基本假设的合理性\\ 基本假设不成立时如何对数据进行修正\\ 判断回归方程拟合的结果\\ 选择回归函数的形式\end{array}\\ 回归变量选择\{\begin{array}{l}自变量选择的标准\\ 逐步分析回归法\end{array}\\ 参数估计方法改进\{\begin{array}{l}偏最小二乘回归\\ 岭回归\\ 主成分回归\end{array}\\ 非线性回归\{\begin{array}{l}一元非线性回归\\ 多段回归\\ 多元非线性回归\end{array}\\ 含有定性变量的回归\{\begin{array}{l}自变量含有定性变量的情况\\ 因变量含有定性变量的情况\end{array}\end{array}$$

  在回归模型中，自变量与因变量具有相关关系，自变量的值是已知的，因变量是要预测的。回归算法的实现步骤和分类算法基本相同，分为学习和预测两个步骤。学习是通过训练样本数据来拟合回归方程的；预测则是利用学习过程中拟合出的回归方程，将测试数据放入方程中求出预测值。

常用的回归模型

回归模型名称	适用条件	算法描述
线性回归	因变量与自变量是线性关系	对一个或多个自变量和因变量之间的线性关系进行建模，可用最小二乘估计法求解模型系数。
非线性回归	因变量与自变量之间不都是线性关系	对一个或多个自变量和因变量之间的非线性关系进行建模。如果非线性关系可以通过简单的函数变换转化成线性关系，则可以利用线性回归的思想求解；如果不能转化，则利用非线性最小二乘估计法求解。
Logistic 回归	因变量一般有 1 和 0 （是与否）两种取值	是广义线性回归模型的特例，利用 Logistics 函数将因变量的取值范围控制在 0~1，表示取值为 1 的概率。
岭回归	参与建模的自变量之间具有多重共线性	是一种改进的最小二乘估计法的方法
主成分回归	参与建模的自变量之间具有多重共线性	主成分回归是根据主成分分析的思想提出来的，是对最小二乘估计法的一种改进，它是参数估计的一种有偏估计。可以消除自变量之间的多重共线性。

sklearn 库内部常用回归算法

模块名称	函数名称	算法名称	官方文档链接
linear_model	LinearRegression	线性回归	官方文档
svm	SVR	支持向量回归	官方文档
neighbors	KNeighborsRegressor	最邻近回归	官方文档
tree	DesionTreeRegressor	回归决策树	官方文档
ensemble	RandomForestRegressor	随机森林回归	官方文档
ensemble	GradientBoostingRegressor	梯度提升回归数	官方文档

# 使用sklearn估计器构建线性回归模型
from sklearn.linear_model import LinearRegression
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split

boston = load_boston()
X = boston['data']
y = boston['target']
names = boston['feature_names']

# 划分数据集
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.2,random_state=125)

# 建立线性回归模型
clf = LinearRegression().fit(X_train,y_train)
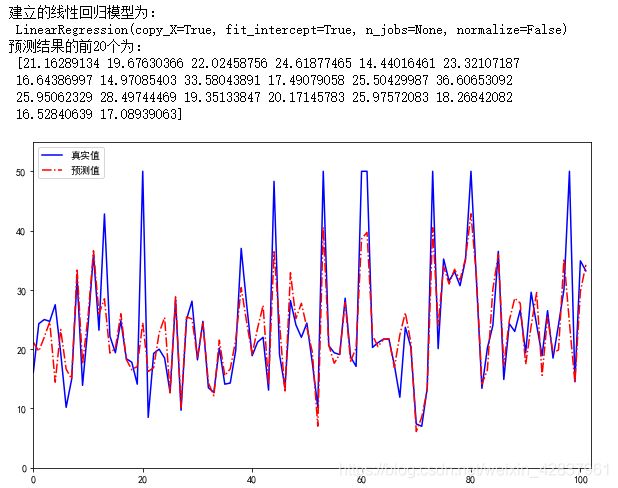
print('建立的线性回归模型为：\n',clf)

# 预测训练接结果
y_pred = clf.predict(X_test)
print('预测结果的前20个为：\n',y_pred[:20])

# 回归结果可视化
import matplotlib.pyplot as plt

plt.rcParams['font.sans-serif'] = 'SimHei'
plt.rcParams['axes.unicode_minus'] = False
plt.figure(figsize=(10,6))
plt.plot(range(y_test.shape[0]),y_test,'b-')
plt.plot(range(y_test.shape[0]),y_pred,'r-.')
plt.xlim((0,102))
plt.ylim(0,55)
plt.legend(['真实值','预测值'])
plt.show()

5.2 评价回归模型

  回归模型的性能评价不同于分类模型，虽然都是对照真实值进行评价，但由于回归模型的预测结果和真实值都是连续的，所以不能够求取 Presision、Recall 和 F1 值等评价指标。回归模型拥有一套独立的评价指标。

metrics 模块提供的回归模型评价指标

sklearn 函数	方法名称	最优值	官方文档链接
mean_absolute_error	平均绝对误差	0.0	官方文档
mean_square_error	均方误差	0.0	官方文档
median_absolute_error	中值绝对误差	0.0	官方文档
explained_variance_score	可解释方差值	1.0	官方文档
r2_score	R2 值	1.0	官方文档

# 回归模型常用的评价方法
from sklearn.metrics import explained_variance_score,mean_absolute_error,mean_squared_error,\
median_absolute_error,r2_score

print('boston数据线性回归模型的平均绝对误差为：',mean_absolute_error(y_test,y_pred))
print('boston数据线性回归模型的均方误差为：',mean_squared_error(y_test,y_pred))
print('boston数据线性回归模型的中值绝对误差为：',median_absolute_error(y_test,y_pred))
print('boston数据线性回归模型的可解释方差值为：',explained_variance_score(y_test,y_pred))
print('boston数据线性回归模型的R方值为：',r2_score(y_test,y_pred))