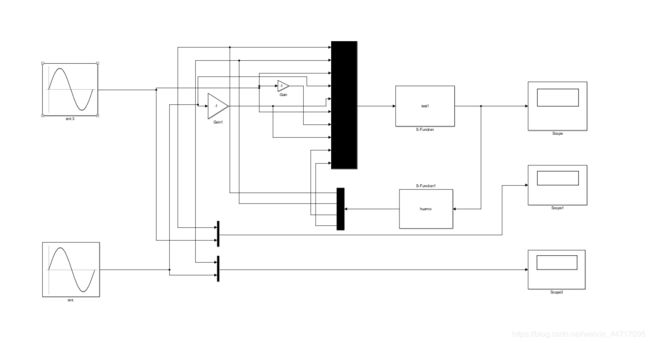
机械手的滑模控制matlab实验

如果可以的话，欢迎关注和点赞哦~

假设机械臂实际物理参数如下

function [sys,x0,str,ts,simStateCompliance] = test1(t,x,u,flag)
switch flag
  case 0  [sys,x0,str,ts,simStateCompliance]=mdlInitializeSizes;
  case 1
    sys=mdlDerivatives(t,x,u);
  case 3
    sys=mdlOutputs(t,x,u);
  case {2,4,9}
    sys=[];
  otherwise
DAStudio.error('Simulink:blocks:unhandledFlag',num2str(flag));
end
function [sys,x0,str,ts,simStateCompliance]=mdlInitializeSizes
sizes = simsizes;		sizes.NumContStates  = 0; 
sizes.NumDiscStates  = 0; sizes.NumOutputs  = 2; sizes.NumInputs  = 10; 	sizes.DirFeedthrough = 1;  
sizes.NumSampleTimes = 1;  
sys = simsizes(sizes);
x0  = [ ];  str = [];	ts  = [0 0];
simStateCompliance = 'UnknownSimState';
 
function sys=mdlDerivatives(t,x,u)
sys=[]
 
function sys=mdlOutputs(t,x,u)
q1=u(1);q2=u(2);q=[q1;q2];qd1=u(3);qd2=u(4);
qd=[qd1;qd2];
dqd1=u(5);dqd2=u(6);dqd=[dqd1;dqd2]; 
ddqd1=u(7);ddqd2=u(8);ddqd=[ddqd1;ddqd2]; 
dq1=u(9);dq2=u(10);
dq=[dq1;dq2];
 
m1=1;l1=1;lc1=0.5;i1=1/12;me=3;lce=1;ie=0.4;ce=0;
e1=-7/12;e2=9.81;
 
a=i1+m1+lc1*lc1+ie+me*lce*lce+me*l1*l1;
b=ie+me*lce*lce;
c=me*l1*lce*cos(ce);
n=me*l1*lce*sin(ce);
 
M=[a+2*c*cos(q2)+2*n*sin(q1) b+c*cos(q2)+n*sin(q2);
b+c*cos(q2)+n*sin(q2) b];
C=[(-2*c*sin(q2)+2*n*cos(q2))*dq2 (-c*sin(q2)+n*cos(q2))*dq2;
(c*sin(q2)-n*cos(q2))*dq1 0 ];
G=[c*e2*cos(q1+q2)+n*e2*sin(q1+q2)+(a-b+e1)*e2*cos(q1);
    c*e2*cos(q1+q2)+n*e2*sin(q1+q2)];

K=[2000 0;0 2000];
lamuda=[25 0;0 25];
y=(K+M*lamuda)*(dqd-dq)+(K*lamuda+C*lamuda)*(qd-q)+M*ddqd+C*dqd+G; 
sys = y;

function [sys,x0,str,ts,simStateCompliance] = huamo(t,x,u,flag)
switch flag
    case 0 [sys,x0,str,ts,simStateCompliance]=mdlInitializeSizes;
    case 1 
        sys=mdlDerivatives(t,x,u);
    case 3
        sys=mdlOutputs(t,x,u);
    case {2,4,9}
        sys=[];
    otherwise
        DAStudio.error('Simulink:blocks:unhandledFlag', num2str(flag));
end
 
function [sys,x0,str,ts,simStateCompliance]=mdlInitializeSizes
   sizes=simsizes;sizes.NumContStates=4;  	sizes.NumDiscStates=0;  sizes.NumOutputs= 4; 	sizes.NumInputs=2;  sizes.DirFeedthrough=0;  
   sizes.NumSampleTimes=1;  sys=simsizes(sizes);
   x0  = [0;0;0;0 ];     str = [];     ts  = [0 0];
   simStateCompliance = 'UnknownSimState';
 
function sys=mdlDerivatives(t,x,u)
 q1=x(1);q2=x(2);dq1=x(3);dq2=x(4);q=[q1;q2];dq=[dq1;dq2];
 %参数
m1=1;l1=1;lc1=0.5;i1=1/12;me=3;lce=1;ie=0.4;ce=0;e1=-7/12;e2=9.81;
a=i1+m1+lc1*lc1+ie+me*lce*lce+me*l1*l1;         b=ie+me*lce*lce;
c=me*l1*lce*cos(ce);                            n=me*l1*lce*sin(ce);
M=[a+2*c*cos(q2)+2*n*sin(q1) b+c*cos(q2)+n*sin(q2);b+c*cos(q2)+n*sin(q2) b];
C=[(-2*c*sin(q2)+2*n*cos(q2))*dq2 (-c*sin(q2)+n*cos(q2))*dq2;(c*sin(q2)-n*cos(q2))*dq1 0 ];
G=[c*e2*cos(q1+q2)+n*e2*sin(q1+q2)+(a-b+e1)*e2*cos(q1);c*e2*cos(q1+q2)+n*e2*sin(q1+q2)];
ling=[0 0;0 0 ];     sys=dx;
dx=[dq;-inv(M)*C*q-inv(M)*G]+[ling;inv(M)]*u;

function sys=mdlOutputs(t,x,u)
sys=[x(1) ; x(2);x(3);x(4)];