机器学习之八大算法⑧——决策树(回归树DecisionTreeRegressor)
回归树代码及注释
import numpy as np
import matplotlib.pyplot as plt
from sklearn.tree import DecisionTreeRegressor #调用回归树模型
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
X = np.linspace(0,5,400).reshape(400,1) #在(0,5)产生400个数的数据集X,并排序
y = np.sin(X) #映射成sin函数
#创建模型
r_tree5 = DecisionTreeRegressor(max_depth=5)
r_tree2 = DecisionTreeRegressor(max_depth=2)
#训练模型
r_tree5.fit(X,y)
r_tree2.fit(X,y)
#求预测值
h2 = r_tree2.predict(X)
h5 = r_tree5.predict(X)
print('max_depths=5准确率:',r_tree5.score(X,y))
print('max_depths=2准确率:',r_tree2.score(X,y))
# 画图
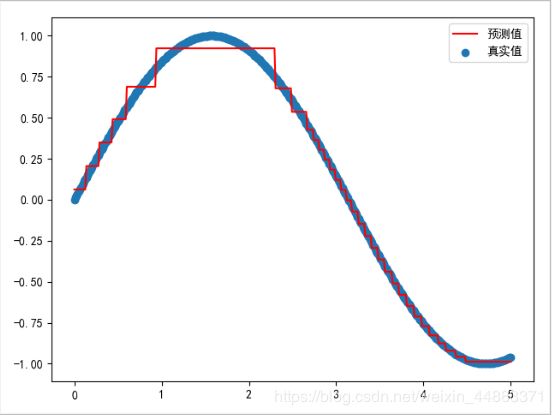
plt.scatter(X,y,label='真实值')
plt.plot(X,h5,c='r',label='预测值')
plt.legend()
plt.show()
效果展示
决策树算法python库实现:
dtr= DecisionTreeRegressor(max_depth=5) #决策树回归器(均方差mse/mae)
dtr= DecisionTreeClassifier(max_depth=5) #决策树分类器(基尼系数或熵)
主要参数:
max_depth: 树最大深度,可选,缺省None,
min_samples_split : 分割内部节点所需最少样本数,可选,缺省2
min_samples_leaf : 成为叶子节点所需最少样本, 可选, 缺省1
max_features : 寻找最佳分割时考虑的特征数目, 可选, 缺省None: float/比例, ‘sqrt’/sqrt(n_features), ‘log2’/log2(n_features)
min_impurity_decrease : 如果节点分割导致不纯度减少超过此值,将进行分割,可选, 缺省0.0
presort : 预排序,加速寻找最佳分割,可选,缺省False, 大数据集降低训练过程, 小训练集或受限深度,可加快训练
random_state: 缺省None; 若int, 随机数产生器seed, 若RandomStates实例, 随机数产生器, 若None, np.random
调用库函数计算:建立模型并计算
dtr.fit(X,y) # 调用库函数决策树算法: 分类器y是整数或string;回归器y是浮点数
dtr.predict(X) # 预测样本类别或回归值,返回shape(n_samples)或(n_samples,n_outputs)
dtr.decision_path(X) #返回决策路径,返回shape = [n_samples, n_nodes]
dtr.score(X, y) #返回预测结果的R^2(1-u/v). u=((y_true - y_pred) ** 2).sum()
v=((y_true - y_true.mean()) ** 2).sum()
dtr.apply(X) # 返回每个样本预测为叶子的索引
dtr.n_features_ # 执行’fit’时的特征数
dtr.n_outputs_ # 执行’fit’时的输出数
dtr.tree_ # 树对象