小嘿嘿之群体智能优化算法

遗传算法

定义

遗传算法（Genetic Algorithm, GA）是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型，是一种通过模拟自然进化过程搜索最优解的方法。

基本知识点

编码

由于遗传算法不能直接处理问题空间的参数,因此必须通过编码将要求解的问题表示成遗传空间的染色体或者个体。这一转换操作就叫做编码。

适应度函数

进化论中的适应度，是表示某一个体对环境的适应能力，也表示该个体繁殖后代的能力。遗传算法的适应度函数也叫评价函数，是用来判断群体中的个体的优劣程度的指标，它是根据所求问题的目标函数来进行评估的。
适应度函数需满足：
a）单值、连续、非负、最大化
b) 合理、一致性
c）计算量小
d）通用性强

算法流程

选择

随机初始化种群后，种群中每个个体代表问题域的一个潜在解，选 择出较优个体进行复制，这体现了达尔文自然选择中“适者生存”的原则。常用 的选择方法有：轮盘赌，随机竞争选择等。

交叉

选出概率较大的两个个体，通过染色体交换生成新的个体，交叉后 的个体保留了父代基本特征。常用的交叉方法有：单点交叉、双点交叉和多点交 叉等。

变异

按照一定的概率对个体的某位置进行变异从而产生新个体，增加了 种群的多样性，提高算法跳出局部最优的能力。常用的变异方法有：基本位突变、 均匀突变等。

粒子群算法（Particle Swarm Optimization,PSO）

转载于https://www.zhihu.com/question/23103725/answer/365298309

背景思想

设想这样一个场景：一群鸟在随机搜素食物，在这个区域里只有一块食物，所有的年都不知道食物在哪里，但是它们知道当前的位置离食物还有多远。最简单有效的策略：寻找鸟群中离食物最近的个体来进行搜索。PSO算法就从这种生物种群行为特性中得到启发并用于求解优化问题。
用一种粒子来模拟上述的鸟类个体，每个粒子可视为N维搜索空间中的一个搜索个体，粒子的当前的位置即为对应优化问题的一个候选解，粒子的飞行过程即为该个体的搜索过程。粒子的飞行速度可根据粒子历史最优位置进行动态调整。粒子仅具有两个属性：速度和位置，速度代表移动的快慢，位置代表移动的方向。每个粒子单独搜寻的最优解叫做个体的极值，粒子群中最优的个体极值作为当前全局最优解。不断迭代，更新速度和位置。最终得到满足终止条件的最优解。

位置和速度迭代公式

参考《基于群体智能的图像多阈值分割方法研究 》–孙敏

算法流程

案例

已知：$y=\frac{x_1^2+x_2^2}{10000}$，求$y$最小值。
第一步：设定粒子规模为50个，社会学习因子和个体学习因子为2，最大迭代次数为800.
第二步：在可行域内随机给定粒子位置。

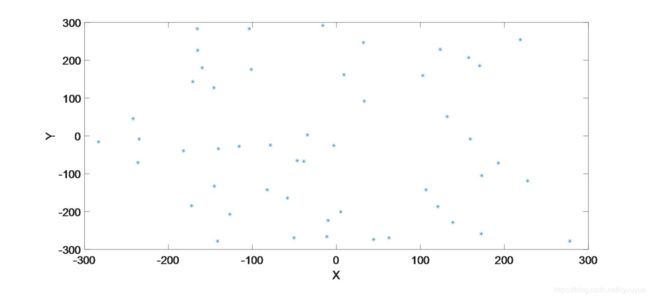
第三步：计算目标函数值，并进行速度和位置更新。

当粒子满足终止条件时，跳出循环输出最优解，在迭代过程中，目标函数是这样变化的

算法在迭代30次后跳出循环，输出最优解[0.0202,0.0426],此时目标函数值为$2.2242\ast 10^{-7}$因为钻用的例子为二次型规划，显然最优解为[0,0]，最优值为0.
下面是三维动画展示的是粒子群算法的寻优过程。

MATLAB代码

clc
clear 
close all
E=0.000001;
maxnum=800;%最大迭代次数
narvs=2;%目标函数的自变量个数
particlesize=50;%粒子群规模
c1=2;%每个粒子的个体学习因子，加速度常数
c2=2;%每个粒子的社会学习因子，加速度常数
w=0.6;%惯性因子
vmax=5;%粒子的最大飞翔速度
v=2*rand(particlesize,narvs);%粒子飞翔速度
x=-300+600*rand(particlesize,narvs);%粒子所在位置
%定义适应度函数
fitness=inline('(x(1)^2+x(2)^2)/10000','x');
for i=1:particlesize
 f(i)=fitness(x(i,:)); 
end
personalbest_x=x;
personalbest_faval=f;
[globalbest_faval,i]=min(personalbest_faval);
globalbest_x=personalbest_x(i,:); 
k=1;
while (k<=maxnum)
 for i=1:particlesize
   f(i)=fitness(x(i,:));
  if f(i)<personalbest_faval(i)
     personalbest_faval(i)=f(i);
   personalbest_x(i,:)=x(i,:);
  end
 end
 [globalbest_faval,i]=min(personalbest_faval);
 globalbest_x=personalbest_x(i,:);
 for i=1:particlesize
  v(i,:)=w*v(i,:)+c1*rand*(personalbest_x(i,:)-x(i,:))...
   +c2*rand*(globalbest_x-x(i,:));
     for j=1:narvs
   if v(i,j)>vmax
    v(i,j)=vmax;
   elseif v(i,j)<-vmax
    v(i,j)=-vmax;
   end  
  end
  x(i,:)=x(i,:)+v(i,:);
    end
        ff(k)=globalbest_faval;
    if globalbest_faval<E
        break
    end
 k=k+1;
end
xbest=globalbest_x;
plot(1:length(ff),ff)

蚁群算法

转载https://blog.csdn.net/m0_37570854/article/details/83715944
是一种用来寻找优化路径的概率型算法，灵感来源于蚂蚁在寻找食物过程中发现路径的行为。这种算法具有分布计算、信息正反馈和启发式搜索的特征，本质上是进化算法中的一种启发式全局优化算法。

背景

蚂蚁会在其经过的路径上释放一种可以称之为“信息素”的物质，蚁群内的蚂蚁对“信息素”具有感知能力，它们会沿着“信息素”浓度较高路径行走，而每只路过的蚂蚁都会在路上留下“信息素”，这就形成一种类似正反馈的机制，这样经过一段时间后，整个蚁群就会沿着最短路径到达食物源了。

算法原理

用蚂蚁的行走路径表示待优化问题的可行解，整个蚂蚁群体的所有路径构成待优化问题的解空间。路径较短的蚂蚁释放的信息素量较多，随着时间的推进，较短的路径上累积的信息素浓度逐渐增高，选择该路径的蚂蚁个数也愈来愈多。最终，整个蚂蚁会在正反馈的作用下集中到最佳的路径上，此时对应的便是待优化问题的最优解。
用人工蚁群算法求解TSP问题时的基本原理是：将m个蚂蚁随机地放在多个城市，让这些蚂蚁从所在的城市出发，n步（一个蚂蚁从一个城市到另外一个城市为1步）之后返回到出发的城市。如果m个蚂蚁所走出的m条路经对应的中最短者不是TSP问题的最短路程，则重复这一过程，直至寻找到满意的TSP问题的最短路径为止。

算法流程

算法相关参数

参数	功能
信息启发因子$\alpha$	反映了蚂蚁在从城市i向城市j移动时，这两个城市之间道路上所累积的信息素在指导蚂蚁选择城市j的程度，即蚁群在路径搜索中随机性因素作用的强度。
期望值启发式因子$\beta$	反映了蚂蚁在从城市i向城市j转移时候期望值${\eta }_{ij}$在指导蚁群搜素中的相对重要程度。其大小反映了蚁群在道路搜素中的先验性、确定性等因素的强弱，$\alpha$、$\beta$ 的大小也会影响算法的收敛性。
蚂蚁总数$m$	在TSP问题中，每次循环当中，每只蚂蚁所走出的每条路径为TSP问题的候选解，m只蚂蚁一次循环所走出来的m条路经为TSP问题的一个解子集，所以这个解子集越大则算法的全局搜索能力越强，但是过大会使算法的收敛速度降低。如果m太小的话，算法也很容易就陷入局部最优，过早的出现停滞现象
信息素总数$Q$	信息素总信息量为蚂蚁循环一周后向经过路径释放信息素的总量
禁忌表$tabu(k)$	用于存放第k只蚂蚁已经走过的城市
概率$p_{ij}^k$	蚂蚁k从当前所在的城市到下一个城市去的概率
信息素${\tau }_{ij}$	城市i和j之间边$e_{ij}$上信息素的残留强度
信息素增量$\Delta {\tau }_{ij}$	一次循环后边$e_{ij}$上信息素的增量
信息素贡献量$\Delta {\tau }_{ij}^k$	一次循环后蚂蚁k对边$e_{ij}$上信息素的贡献量
距离$d_{ij}$	城市i到城市j之间的距离
能见度${\eta }_{ij}$	反映了由城市i转移到城市j的启发程度
信息残留系数$\rho$	由于蚂蚁释放的信息量回随着时间的转移而逐渐挥发，以至于路径上的信息素不能无限递增，该系数太小时会降低算法的全局搜素能力，过大时容易使算法陷入局部最优，影响全局搜素能力。

关键步骤

1上面讲了蚂蚁在选择下一个要转移的城市时候是基于概率选择的，当然这个概率不是随机概率，而是其中的一些参数来决定。假定在t时刻，蚂蚁从目前所在的i城市要选择转移去的下一个j城市，概率大小为$p_{ij}^k$：

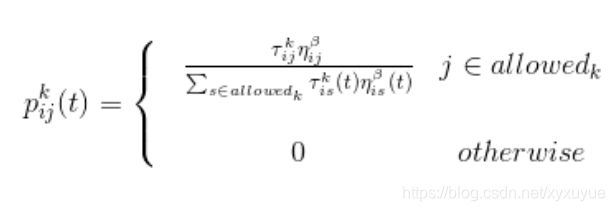
其中$allowe{d}_k$表示允许蚂蚁k下一步可容许去的城市的集合，${\tau }_{ij}^{\alpha }$为边$e_{ij}$上的信息素因数，${\eta }_{ij}^{\beta }$为城市i，j间能见度因数。至于这个过程具体是怎么实现的，在程序中会有相关的源码。
**2、**对任意两个城市i，j之间道路对应的边$e_{ij}$信息素增量按照下式进行：

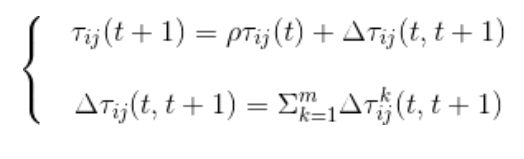
其中，$\Delta {\tau }_{ij}^k(t,t+1)$为蚂蚁k对边上$e_{ij}$所贡献的信息素增量，$\Delta {\tau }_{ij}(t,t+1)$是经过边$e_{ij}$的所有蚂蚁对边$e_{ij}$的信息素量贡献，$\rho$ 为信息素残留系数。对于$\Delta {\tau }_{ij}^k(t,t+1)$的调整方式不同，可以将蚁群算法分为三种模型：蚁密模型、蚁量模型和蚁周模型。
(1)蚁密模型

(2)蚁量模型

(3)蚁周模型

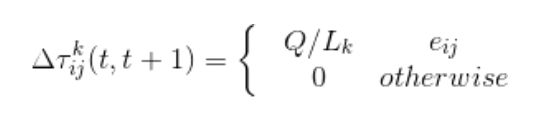
MATLAB代码实现

%算法的第一步是先初始化
clear
m=50;                                   %蚂蚁总数
alpha=1;                                %信息度启发因子
beta=2;                                  %期望值启发式因子
Rho=0.6;                                %信息素挥发因子 
NC_max=100;                         %最大循环次数
Q=80;                                      %信息素增量
C=[5.326,2.558;
4.276,3.452; 
4.819,2.624; 
3.165,2.457; 
0.915,3.921;
4.637,6.026;
1.524,2.261;
3.447,2.111; 
3.548,3.665; 
2.649,2.556;
4.399,1.194; 
4.660,2.949;
1.479,4.440;
5.036,0.244;
2.830,3.140;  
1.072,3.454;  
5.845,6.203; 
0.194,1.767;  
1.660,2.395;
2.682,6.072];%20个城市
% 初始化

n=size(C,1);                            %表示n个城市
D=zeros(n,n); 
for i=1:n 
    for j=1:n
        if i~=j                         %表示同一个城市之间的距离不存在
            D(i,j)=((C(i,1)-C(j,1))^2+(C(i,2)-C(j,2))^2)^0.5;
        else 
             D(i,j)=eps; 
     	end 
   end
end
Eta=1./D;                               %城市与城市之间的能见度，在基于概率转移时用到这个参数
Nc=1;                                   %循环计数
Tau=ones(n,n);                          %信息素浓度矩阵——n*n的单位阵
Tabu=zeros(m,n);                        %禁忌表  ——m*n的零阵
Road_best=zeros(NC_max,n);              %每次循环最佳路径 最大循环次数*n个城市零阵
Roadlength_best=inf.*ones(NC_max,1);    %每次循环最佳路径的长度  最大循环次数*1 单位阵
Roadlength_ave=zeros(NC_max,1);         %每次循环的路径的平均值%将蚂蚁随机分布在n个城
while Nc<=NC_max                        %小于最大循环次数就继续执行
     randpos=[];                            
     for i=1:(ceil(m/n))                 %分多少次将蚂蚁分布完        
     	  randpos=[randpos,randperm(n)];  %循环产生的是20个城市的随机数，都在一行
      end
Tabu(:,1)=(randpos(1,1:m));         %取前m个城市编号
%每只蚂蚁基于概率选择转移去下一个j城市  
      for j=2:n                           %从第二个城市开始选择
	    for i=1:m
	         visited=Tabu(i,1:(j-1));    %表示已经经过的城市，初始化是出发城市
	         J=zeros(1,(n-j+1));         %存放还没有经过的城市  1*19.....1 零阵
	         P=J; 
	         c=1;                                 
	         for k=1:n                                  
	              if length(find(visited==k))==0  %查找已经经过的城市里面有没有k                    
	                  J(Jc)=k;            %没有的话，就把城市k记录进未经过城市矩阵里面                    
	                  Jc=Jc+1;                           
	          end            
	     end
%计算待选城市的概率          
            for k=1:length(J)
 P(k)=(Tau(visited(end),J(k))^alpha)*(Eta(visited(end),J(k))^beta);               %目前经过的城市到下一个所有城市的概率大小           end           P=P/sum(P);           %按照概率选取下一个城市           Pcum=cumsum(P);                         select=find(Pcum>=rand);                to_visit=J(select(1));                           Tabu(i,j)=to_visit;                  end    end    if Nc>=2                                   Tabu(1,:)=Road_best(Nc-1,:);        end%记录本次迭代最佳路线  L=zeros(m,1);  for i=1:m      R=Tabu(i,:);                      %第一只蚂蚁的路线赋给矩阵R      for j=1:(n-1)                               L(i)=L(i)+D(R(j),R(j+1));     %每一只蚂蚁所走的路径长度      end      L(i)=L(i)+D(R(1),R(n));           %加上最后一个点到起始点的路径  end  Roadlength_best(Nc)=min(L);           %本次循环的所有路径中的最短路径放在Roadlength_best中  pos=find(L==Roadlength_best(Nc));     %找出最短路径的所有蚂蚁  Road_best(Nc,:)=Tabu(pos(1),:);       %只取第一只蚂蚁的路径  Roadlength_ave(Nc)=mean(L);           %本次循环所有路径的平均值  Nc=Nc+1;                                % 跟新信息素  delta_Tau=zeros(n,n);                  for i=1:m                                   for j=1:(n-1)          delta_Tau(Tabu(i,j),Tabu(i,j+1))=delta_Tau(Tabu(i,j),Tabu(i,j+1))+Q/L(i);      end      delta_Tau(Tabu(i,n),Tabu(i,1))=delta_Tau(Tabu(i,j),Tabu(i,j+1))+Q/L(i);  end  Tau=(1-Rho).*Tau+delta_Tau;          %这里运用的是蚁周模型   
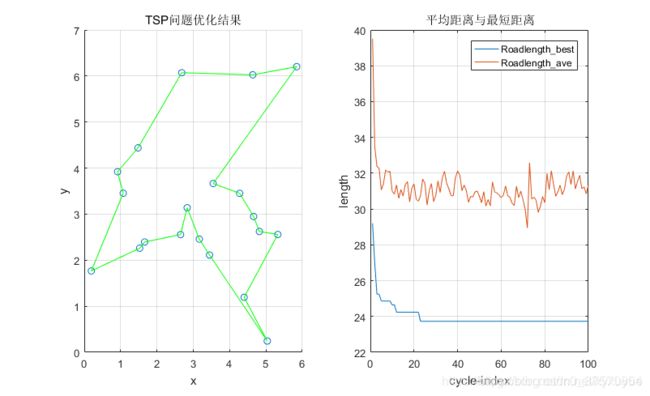
% 禁忌表清零                                   Tabu=zeros(m,n);                   endpos=find(Roadlength_best==min(Roadlength_best));shortest_route=Road_best(pos(1),:);shortest_length=Roadlength_best(pos(1)); figure(1)subplot(1,2,1)% subplot(1,2,1)N=length(R);scatter(C(:,1),C(:,2));hold onplot([C(shortest_route(N),1),C(shortest_route(1),1)],[C(shortest_route(N),2),C(shortest_route(1),2)],'g');hold onfor ii=2:N    plot([C(shortest_route(ii-1),1),C(shortest_route(ii),1)],[C(shortest_route(ii-1),2),C(shortest_route(ii),2)],'g');    hold onendgrid ontitle('TSP问题优化结果');xlabel('x')ylabel('y')subplot(1,2,2)plot(Roadlength_best)hold onplot(Roadlength_ave)grid ontitle('平均距离与最短距离')legend('Roadlength\_best','Roadlength\_ave')xlabel('cycle-index')ylabel('length')

经过100次循环，对20个城市求最优路径，结果是23.70，执行之后的效果图如下：

布谷鸟算法

转载
1、https://blog.csdn.net/zyqblog/article/details/80905019
2、https://blog.csdn.net/sj2050/article/details/98496868

背景

布谷鸟算法的启发当然来自于布谷鸟，因为布谷鸟这种鸟很有意思，生出来的孩子自己不养，直接被扔到其他鸟的鸟巢中去了，但有时候，这些布谷鸟蛋会被被寄宿的那些鸟妈妈发现，然后就被抛弃，有时候，这些宿主会直接放弃整个鸟巢寻找新住处。然而道高一尺魔高一丈，有些品种的布谷鸟生下来的布谷鸟蛋的颜色能和去寄宿的鸟的鸟蛋颜色很相似，并且布谷鸟的破壳时间往往比那些宿主的鸟蛋早，这样，一旦小布谷鸟破壳，它就会将一些鸟蛋扔出鸟巢去以求获得更多的食物，并且，小布谷鸟能模拟宿主鸟孩子的叫声来骗取更多的食物！简单来说，就是如何更高效地去骗吃骗喝。

-他们假设最初在可行域内随机生成一组点（布谷鸟）
-计算这些点的适应值（鸟的健康程度），并记录下最健康鸟的位置及其适应值
-然后通过某种方式更新这些点的位置（布谷鸟找其他鸟的鸟巢下蛋）
-这些寄宿到其他鸟的布谷鸟蛋有一定几率被抛弃，这时布谷鸟需要找新的位置来下新的布谷鸟蛋，没被发现的布谷鸟蛋就保持原样（也就是保持每次迭代的点的总数不变）
-这些布谷鸟蛋成功被孵化然后长大，原有的布谷鸟则会死去，现在评估新的这些点的适应值（新长大的布谷鸟的健康程度），若比原有记录下最好适应值要好则更新最好适应值
-新的这批布谷鸟从第3步继续迭代，直至满足迭代次数或精度要求

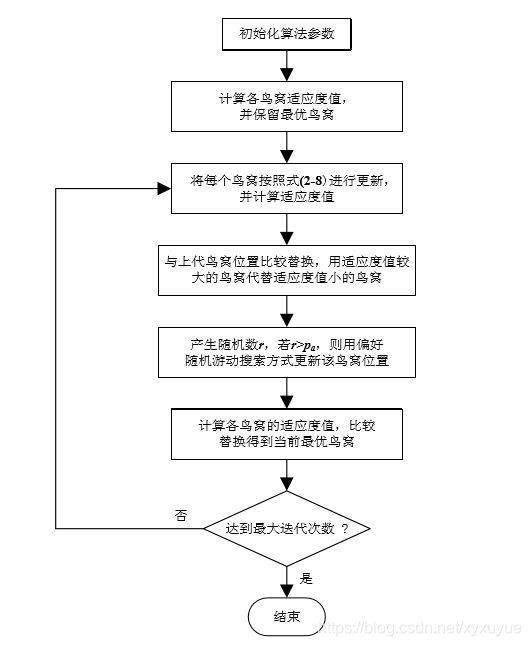
算法流程

莱维飞行

莱维飞行是由较长时间的短步长和较短时间的长步长组成。

从上面的动画中我们可以看到，点大多数时间都只有小距离移动，偶尔会有大距离移动的情况。这和自然界中大多数动物觅食方式方式类似，也就是找到一块区域后细致的查找猎物，如果没找到，就换一片区域找。
那么，该如何实现这种移动方式呢？我们现在假设我们就是捕食者，需要捕猎去了，但尚不清楚猎物在哪，那好，我们先随机选个方向（服从均匀分布，因为在不知道任何信息前提下，对于我们来说各个方向存在猎物的可能性相等），接下来就得确定要走多远了，根据上面的思想，Levy分布要求大概率落在值比较小的地方，而小概率落在值比较大的地方，Mantegna就提出了近似满足这种分布的计算公式：
$s=\frac{u}{|v{|}^{\frac{1}{\beta }}}$
说明：$u\backsim N(0,{\sigma }_u)$,$v\backsim N(0,{\sigma }_v)$,其中，${\sigma }_u={\frac{\Gamma (1+\beta )sin(\frac{\pi \beta }{2})}{\Gamma [\frac{1+\beta }{2}\beta \ast 2^{\frac{\beta -1}{2}}]}}^{\frac{1}{\beta }}$,${\sigma }_v=1$
实现莱维飞行，一要通过均匀概率分布生成一个方向，二要确认步长！

位置更新

• 一个是布谷鸟寻找鸟窝下蛋的寻找路径是采用早已就有的萊维飞行，所以采用萊维飞行更新鸟窝位置的公式被定义如下：
  $X_{t+1}=X_t+\alpha ⨂Levys(\beta )$
  其中 , α是步长缩放因子，Levy(β)是萊维随机路径，⨂就是点乘运算
• 另一个是宿主鸟以一定概率Pa发现外来鸟后重新建窝的位置路径，这个路径可以用萊维飞行或者随机方式，(本文采用随机) , 除此之外，这个位置普遍采用偏好随机游动的方式，即利用了其他鸟窝的相似性。所以新建的鸟窝的位置的公式被定义如下：
  $X_{t+1}=X_t+rHeaviside(Pa-ϵ)⨂(X_i-X_j)$
  其中，r,ϵ 是服从均匀分布的随机数，Heaviside(x) 是跳跃函数(x>0,=1;x<0,=0) , Xi,Xj 是其他任意的连个鸟窝。

算法

案例

x,y in(-3,3),求最大值
**第一步：**先在可行域内随机生成5个点

**第二步：**计算它们的适应度（适应值函数就取上面那个要优化的函数）

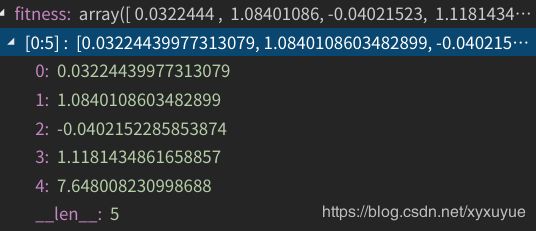
从中挑出最好的并记录下来，我们可以看到，最好的适应值为下标4对应的点，为7.648。
第三步：利用莱维飞行更新点，莱维飞行公式中的$\beta$取为1.5，剩下的把公式敲上去获得步长，但是，这样生成的步长的规格是大于问题的规模的，后面我们需要调参，但这里为了简便我就把我后来调出来的结果摆出来，莱维飞行的步长需要乘以系数0.4才能让莱维飞行不至于走的太放飞自我，也不至于走的太畏畏缩缩（多数情况下，系数取为0.1和0.01）。这里我们还用到了一个小技巧，我们当然是希望上一轮产生的最好点能在下一轮保留下来，所以我们可以在步长前乘以个系数$(x_i^{上一轮}-x_{best}^{上一轮})$，这里的i就是步长对应的点下标。当然，有了步长还不够，还得有个步长方向，这个方向我们就用0-1均匀概率分布产生，步长方向（矢量）点乘步长（矢量）就是步长增量。这是莱特飞行更新后的结果：

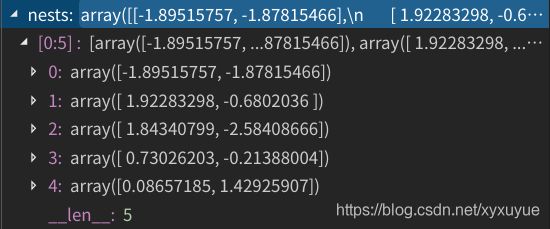
**第四步：**接下来，一些布谷鸟蛋可能会被宿主发现并被抛弃，这个抛弃的概率$P_a$我们设置为0.25，当有布谷鸟蛋被抛弃时，我们需要寻找新的寄宿地点，而寻找新的寄宿地点的算法就是上面提到的局部随机行走算法，我们可以把$\alpha$这个系数定为1，步长s我们也取为1，后面两个随机选取的点$x_j^t$,$x_k^t$我们通过均匀概率分布选出，这里我们不使用跃迁函数H。更新后的结果如下：

**第五步：**计算这些新点的适应值，并挑出最大值和记录的最好点的适应值比较，若该轮更新得到的最大值更好，则将该轮得到的最大点设为最好点并记录下来。遗憾的是，这里，该轮点的最大值没有比记录的最好点好，所以我们不用更新最好点的值。

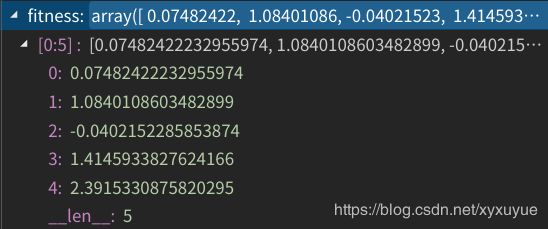
**第六步：**回到上面的第三步，继续循环直至满足迭代次数要求或精度要求。

**补充：**由于随机行走（莱维飞行是随机行走的一种特殊形式）可能会超出我们的可行域范围，我们可以利用简单的边界条件，即当点超过下边界时，则用下边界的值代替，同理，当点超过上边界时，则用上边界的值代替。

源码下载

https://download.csdn.net/download/g425680992/10517545