- 【机器学习笔记Ⅰ】6 多类特征
巴伦是只猫
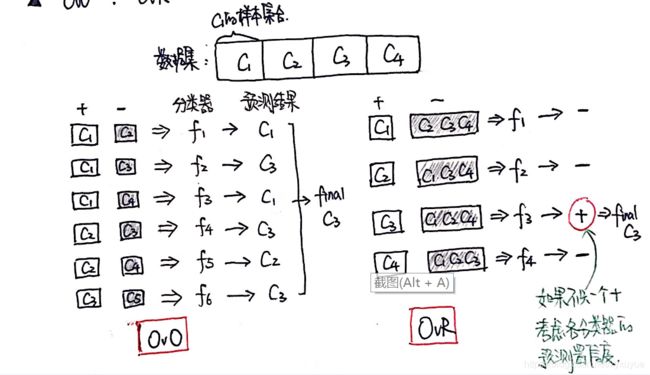
机器学习机器学习笔记人工智能
多类特征(Multi-classFeatures)详解多类特征是指一个特征(变量)可以取多个离散的类别值,且这些类别之间没有内在的顺序关系。这类特征是机器学习中常见的数据类型,尤其在分类和回归问题中需要特殊处理。1.核心概念(1)什么是多类特征?定义:特征是离散的、有限的类别,且类别之间无大小或顺序关系。示例:颜色:红、绿、蓝(无顺序)。城市:北京、上海、广州(无数学意义的大小关系)。动物类别:猫
- UIView和CALayer是啥关系
有没有人告诉你
1.首先UIView可以响应事件,Layer不可以.UIKit使用UIResponder作为响应对象,来响应系统传递过来的事件并进行处理。在UIResponder中定义了处理各种事件和事件传递的接口。UIApplication、UIViewController、UIView、和所有从UIView派生出来的UIKit类(包括UIWindow)都直接或间接地继承自UIResponder类。CALaye
- 企业级视频链接的技术实现与安全性策略
前言视频链接作为内容分发的关键入口,其参数设计直接影响系统安全性、用户体验和运营效率。一个标准化的视频链接应包含资源标识、访问控制和播放体验三类核心参数,同时保持结构清晰和可扩展性。视频链接的批量生成与管理策略1.高效批量生成技术针对运营场景的批量链接生成需求,实现高性能的生成方案:importcsvimportconcurrent.futuresfromtqdmimporttqdmclassBa
- react中的this指向问题
匀升ovo
reactreact.jsjavascript前端
react中this指向问题对于class来说,在class中定义的方法实际上绑定在类的原型中(prototype),我需要通过class的实例调用这个方法才能拿到实例的this例如下方代码classPersonextendsReact.Component{constructor(props){super(props);this.state={name:props.name}}render(){r
- 【Python】memory_profiler
宅男很神经
python开发语言
1.1引用计数与垃圾回收:Python的“贴身管家”与“清洁工”Python,特别是其标准实现CPython,其内存管理的核心是建立在一个优雅而高效的组合机制之上的:以引用计数为主,分代垃圾回收为辅。1.引用计数(ReferenceCounting):主要的内存管家这是CPython内存管理的基石。其原理极其简单:CPython中的每一个对象(一个整数、一个列表、一个自定义类的实例),其内部都维护
- Android PNG/JPG图ARGB_8888/RGB_565解码形成Bitmap在物理内存占用大小的简单计算
AndroidPNG/JPG图ARGB_8888/RGB_565解码形成Bitmap在物理内存占用大小的简单计算Android的Bitmap是一个用于表示图像数据的核心类,代表一张图片在内存中的存储,Bitmap存储了图像的像素信息数据。Bitmap把图像理解为像素点组成的二维矩阵,每个像素点存储对应位置的一系列ARGB值(透明度+红绿蓝通道)。Bitmap在内存中占用大小的关键计算公式:内存
- python炫酷烟花表白源代码,html代码烟花特效python
liuyifan0
pygamepython开发语言
大家好,小编来为大家解答以下问题,python绘制烟花特定爆炸效果,python炫酷烟花表白源代码,今天让我们一起来看看吧!代码实现:importpygameimportrandomimportmath#屏幕宽度SCREEN_WIDTH=1350SCREEN_HEIGHT=800#烟花颜色COLORS=[(255,0,0),(0,255,0),(0,0,255),(255,255,0),(255,
- 定时器和守护线程
(八)定时器标准库中的定时器标准库中提供了一个Timer类。Timer类的核心方法为schedule,schedule包含两个参数:第⼀个参数指定即将要执行的任务代码,第⼆个参数指定多长时间之后执行(单位为毫秒)。Timertimer=newTimer();timer.schedule(newTimerTask(){@Overridepublicvoidrun(){System.out.print
- 深度解析:Java内部类与外部类的交互机制
hi星尘
javajava交互开发语言
1.内部类概述在Java中,**内部类(InnerClass)**是定义在另一个类内部的类。根据是否依赖外部类实例,内部类可分为:非静态内部类(成员内部类):持有外部类的隐式引用,可访问其成员。静态内部类(StaticNestedClass):不依赖外部类实例,需显式传递引用。局部内部类(LocalClass):定义在方法或作用域内。匿名内部类(AnonymousClass):无类名,直接实例化。
- C#-Type&Assembly
霸王奉先
C#c#开发语言TypeAssembly程序集反射类反射
一.TypeDLL文件在被加载至内存时每一个类都有一个Type,根据Type可获取类的方法,字段等信息.<1.获取所有字段#获取string类对应TypeTypetype=typeof(string);#获取私有字段,公有字段,静态字段FieldInfo[]allFields=type.GetFields(BindingFlags.Public|BindingFlags.NonPublic)<2.
- Vue动态绑定Class与Style
一、动态绑定Class1.1对象语法v-bind:class指令是Vue.js中用于动态绑定CSS类的指令。它可以根据Vue实例中的数据来动态添加或移除HTML元素的类。这样可以根据数据的变化来动态改变元素的样式,实现更灵活的样式控制。语法class-name:要绑定的CSS类名condition:一个表达式,当为true时,class-name会被添加;当为false时,class-name会被
- 游戏引擎中顶点着色&像素着色
霸王奉先
游戏开发基础理论游戏引擎顶点着色器像素着色器顶点颜色顶点UV顶点法向
一.GPU渲染管线GPU在接收到游戏端提交的Mesh,Shader数据后,渲染管线开始工作,将数据进行处理投射为2D屏幕中光栅图像.GPU硬件中着色单元有两类,分别为顶点着色器和像素着色器.二.顶点着色器完成Mesh网格中顶点(3D)到屏幕(2D)计算vertex_fvf(灵活顶点格式)=3D坐标+法向+UV+颜色(布料,摇曳等特殊效果)+自定义structVetex_Fvf{floatx,y,z
- Java自定义类热加载实现原理与实践
weixin_ab
#类的加载机制java类加载
Java自定义类热加载实现原理与实践在Java开发中,类热加载(ClassReloading)指在程序运行时动态替换已加载的类,避免重启应用。核心原理是通过自定义类加载器打破JVM类加载的固有规则,实现类的动态加载与更新。以下从实现原理、核心步骤、代码示例到生产实践展开详细解析。一、热加载核心原理:突破类加载机制限制1.类加载器的隔离性每个类加载器维护独立的命名空间,相同类名的类由不同加载器加载会
- Spring Boot类加载机制深度剖析
weixin_ab
#类的加载机制java类加载
SpringBoot类加载机制深度剖析:从可执行Jar到自动配置的实现原理SpringBoot通过对Java类加载机制的定制化扩展,实现了可执行Jar包运行、自动配置、热部署等核心特性。其类加载机制既保留了JVM标准规范,又针对微服务架构和嵌入式容器进行了优化,以下从架构设计、核心组件、典型场景到源码实现展开深度解析。一、SpringBoot类加载器体系架构(对比独立Tomcat)1.简化的两层类
- 145、将程序划分为模块:深入理解C++中的模块化编程
raspberrypi5
C++编程入门与实践C++模块化编程头文件
将程序划分为模块:深入理解C++中的模块化编程1.模块化编程的意义在软件开发中,将大型程序划分为较小的模块是一种常见的实践。这种做法不仅提高了代码的可维护性和可读性,还便于团队协作。通过将功能分离到不同的模块中,开发者可以专注于特定的功能实现,而不必担心整个程序的复杂性。此外,模块化编程还有助于代码的重用,减少了冗余代码的编写。优点总结减少编译时间:小模块可以更快地编译,特别是对于大型项目,整体编
- 【MySQL】索引(B+树详解)
Brookty
MySQL数据结构mysql数据库后端学习b树数据结构
MySQL(五)索引一、索引的减I/O设计1.读取量2.搜索树2.1方向2.2有序3.分多叉3.1B树弊端:3.2B+树3.2.1非叶子-搜索字段3.2.1.1海量分叉3.2.1.1.1最大式3.2.1.1.2最快式3.2.1.2缓存内存3.2.1.2.1字段总量小3.2.1.2.2时间复杂度3.2.1.3区间搜索向下保留3.2.1.3.1过程3.2.1.3.2模式3.2.1.3.3效果3.2.2
- c++ python 共享内存
qianbo_insist
音视频和c++java物联网c++c++python开发语言
一、目的是为了c++来读取并解码传递给python,Python做测试非常方便,c++和python之间必须定好协议,整体使用c++来解码,共享内存传递给python二、主类主类,串联decoder,注意decoder并没有直接在显存里面穿透,是解码以后传递给内存,从内存传给python#pragmaonce#define__STDC_CONSTANT_MACROS#defineSDL_MAIN_
- Coze智能体开发:如何批量生成和处理图片
王国平
CozeAIAgent智能体开发语言模型人工智能开发语言智能体Agent
在绘本制作、图片后期制作等场景中,往往需要使用模型来批量生成和处理图片。扣子提供了多个图像处理类节点,支持图像生成、添加水印、画质优化等多种常见的图片处理方式,你可以在批处理节点中嵌套图像生成等图像处理节点,实现图片的批量操作。本文档以绘本制作工作流为例,演示如何通过批处理节点和图像节点实现图像的批量生成和批量处理。效果演示通过绘本制作工作流,你可以批量生成类似以下风格的图片。搭建过程中你也可以根
- 主流 3D 感知技术对比-iTOF、dTOF、结构光、激光雷达
moonsims
数码相机
主流3D感知技术对比-iTOF、dTOF、结构光、激光雷达四类主流3D感知技术对比表对比维度iToF相机dToF相机固态LiDAR+可见光融合结构光相机测距原理连续调制光→相位差计算激光脉冲→飞行时间测距激光扫描点云+图像纹理融合投射编码光图案+视差三角测量代表设备IntelD435i,AzureKinectSTVL53L5CX,SonyIMX611L3CAM,RoboSenseM1+RGBRea
- Gradio全解5——Interface:高级抽象界面类(上)
龙焰智能
Gradio全解教程InterfaceAPI参数成员函数launchloadfrom_pipelineintergrate
Gradio全解5——Interface:高级抽象界面类(上)前言5.Interface:高级抽象界面类5.1Interface类详解5.1.1Interface示例1.代码及运行2.代码解析5.1.2InterfaceAPI参数5.1.3Interface类成员函数1.launch()2.load()3.from_pipeline()4.integrate()5.queue()参考文献前言本系列
- Kafka Controller 元数据解析与故障恢复实战指南
磐基Stack专业服务团队
Kafkakafkalinq分布式
#作者:张桐瑞文章目录1生产案例:Controller选举在故障恢复中的关键作用1.1问题背景1.2核心操作原理:2Controller元数据全景:从ZooKeeper到内存的数据镜像2.1元数据核心载体:ControllerContext类2.2核心元数据深度解析1生产案例:Controller选举在故障恢复中的关键作用1.1问题背景某Kafka集群部分核心主题分区一直处于“不可用”状态,通过k
- unity进阶学习笔记:消息框架
Raine_Yang
unity学习笔记unity游戏引擎c#单例模式泛型
1使用消息框架的目的对于小型游戏,可能不需要任何框架,而是让各个游戏脚本直接相互通信。如要实现玩家受到攻击血量减少,通过玩家控制类向血条脚本发送消息减少血量。但是这样直接通信会导致各脚本通信关系记为复杂,并且每一个脚本都和多个脚本有联系,导致维护和更新十分困难我们利用上节课讲的管理类,可以将一类脚本由一个管理类控制,如将玩家的功能放在玩家管理类下,将血条,背包等UI组件放在UI管理类下。这样要减少
- Python 基础入门第十三讲 魔法方法补充、单例模式、reflect反射(getattr、hasattr、__import__())
第十三讲一、特殊成员和魔法方法在之前的课程中已经学习过如__init__、__str__、__dir__等魔法方法,现补充一些常用的魔法方法:1.__doc__魔法方法该魔法方法的作用为打印类的说明文档,举个例子:print(str().__doc__)###输出结果为:str(object='')->strstr(bytes_or_buffer[,encoding[,errors]])->str
- python魔法方法长文详解
千翻娃儿
python原生基础python
python魔法方法详解1.什么是魔法方法魔法方式(Magicmethods)是python的内置函数,一般以双下划线开头和结尾,比如__add__,__new__等。每个魔法方法都有对应的一个内置函数或者运算符。当我们个对象使用这些方法时,相当于对这个对象的这类方法进行重写(如运算符重载)。魔法方法的存在是对类或函数进行了提炼,供python解释器直接调用。当使用len(obj)时,实际上调用的
- 免费棱光 PDF:免安装 加水印 去水印 批量格式转换
小瑞软件库
开源软件电脑软件构建
各位办公小能手们,今天给大家介绍一款超棒的PDF处理工具——棱光PDF!它完全免费,专门解决咱对PDF文件的常见操作需求。绿色免安装,体积小得跟颗花生米似的,打开就能用。它有三大核心功能,分别是水印管理、格式转换和批量处理。软件下载地址安装包先说说水印处理,你可以给PDF文件加上自定义的文字或者图片水印,还能随便调整水印的位置、大小和透明度。要是文档里已经有水印,它也能精准识别,然后一键清除。,把
- Axure版ArcoDesign 组件库-免费版
AxureMost
axure模板-素材axure产品经理
ArcoDesign元件库是字节系基于ByteDesign升级而来的、能力全面的企业级产品设计系统。以下是对它的详细介绍:链接地址特点丰富的组件和样式:包含各种类型的组件,覆盖了多种交互场景,如通用类、布局类、数据展示类、数据输入类、反馈类、导航类等。同时提供丰富的颜色主题配置,支持自定义,包括基础颜色、字体、阴影等,且支持可视化编辑与实时预览。灵活的布局方案:基于模块化设计,支持响应式设计,便于
- 机器学习21-线性网络思考
坐吃山猪
机器学习机器学习人工智能线性网络
机器学习21-线性网络思考针对线性网络的发展问题,进行补充学习1-核心知识点1-传统机器学习针对线性分类算法求解的方式有哪些?请详细列举不同的算法对应的损失函数和计算思路在传统机器学习中,线性分类算法是一种非常重要的方法,用于将数据划分为不同的类别。以下是几种常见的线性分类算法,包括它们的损失函数和计算思路:1.感知机(Perceptron)损失函数感知机的损失函数是基于误分类点的,其目标是最小化
- 【雕爷学编程】MicroPython手册之 ESP32-CAM 机器人目标跟踪
驴友花雕
机器人目标跟踪人工智能嵌入式硬件pythonMicroPythonESP32-CAM
MicroPython是为了在嵌入式系统中运行Python3编程语言而设计的轻量级版本解释器。与常规Python相比,MicroPython解释器体积小(仅100KB左右),通过编译成二进制Executable文件运行,执行效率较高。它使用了轻量级的垃圾回收机制并移除了大部分Python标准库,以适应资源限制的微控制器。MicroPython主要特点包括:1、语法和功能与标准Python兼容,易学
- 【雕爷学编程】MicroPython手册之 ESP32-S3 USB摄像头
驴友花雕
嵌入式硬件单片机pythonMicroPythonESP32-S3USB摄像头
MicroPython是为了在嵌入式系统中运行Python3编程语言而设计的轻量级版本解释器。与常规Python相比,MicroPython解释器体积小(仅100KB左右),通过编译成二进制Executable文件运行,执行效率较高。它使用了轻量级的垃圾回收机制并移除了大部分Python标准库,以适应资源限制的微控制器。MicroPython主要特点包括:1、语法和功能与标准Python兼容,易学
- 【雕爷学编程】MicroPython手册之 ESP32-CAM 图像识别
驴友花雕
1024程序员节单片机嵌入式硬件MicroPythonpythonESP32-CAM图像识别
MicroPython是为了在嵌入式系统中运行Python3编程语言而设计的轻量级版本解释器。与常规Python相比,MicroPython解释器体积小(仅100KB左右),通过编译成二进制Executable文件运行,执行效率较高。它使用了轻量级的垃圾回收机制并移除了大部分Python标准库,以适应资源限制的微控制器。MicroPython主要特点包括:1、语法和功能与标准Python兼容,易学
- java解析APK
3213213333332132
javaapklinux解析APK
解析apk有两种方法
1、结合安卓提供apktool工具,用java执行cmd解析命令获取apk信息
2、利用相关jar包里的集成方法解析apk
这里只给出第二种方法,因为第一种方法在linux服务器下会出现不在控制范围之内的结果。
public class ApkUtil
{
/**
* 日志对象
*/
private static Logger
- nginx自定义ip访问N种方法
ronin47
nginx 禁止ip访问
因业务需要,禁止一部分内网访问接口, 由于前端架了F5,直接用deny或allow是不行的,这是因为直接获取的前端F5的地址。
所以开始思考有哪些主案可以实现这样的需求,目前可实施的是三种:
一:把ip段放在redis里,写一段lua
二:利用geo传递变量,写一段
- mysql timestamp类型字段的CURRENT_TIMESTAMP与ON UPDATE CURRENT_TIMESTAMP属性
dcj3sjt126com
mysql
timestamp有两个属性,分别是CURRENT_TIMESTAMP 和ON UPDATE CURRENT_TIMESTAMP两种,使用情况分别如下:
1.
CURRENT_TIMESTAMP
当要向数据库执行insert操作时,如果有个timestamp字段属性设为
CURRENT_TIMESTAMP,则无论这
- struts2+spring+hibernate分页显示
171815164
Hibernate
分页显示一直是web开发中一大烦琐的难题,传统的网页设计只在一个JSP或者ASP页面中书写所有关于数据库操作的代码,那样做分页可能简单一点,但当把网站分层开发后,分页就比较困难了,下面是我做Spring+Hibernate+Struts2项目时设计的分页代码,与大家分享交流。
1、DAO层接口的设计,在MemberDao接口中定义了如下两个方法:
public in
- 构建自己的Wrapper应用
g21121
rap
我们已经了解Wrapper的目录结构,下面可是正式利用Wrapper来包装我们自己的应用,这里假设Wrapper的安装目录为:/usr/local/wrapper。
首先,创建项目应用
&nb
- [简单]工作记录_多线程相关
53873039oycg
多线程
最近遇到多线程的问题,原来使用异步请求多个接口(n*3次请求) 方案一 使用多线程一次返回数据,最开始是使用5个线程,一个线程顺序请求3个接口,超时终止返回 缺点 测试发现必须3个接
- 调试jdk中的源码,查看jdk局部变量
程序员是怎么炼成的
jdk 源码
转自:http://www.douban.com/note/211369821/
学习jdk源码时使用--
学习java最好的办法就是看jdk源代码,面对浩瀚的jdk(光源码就有40M多,比一个大型网站的源码都多)从何入手呢,要是能单步调试跟进到jdk源码里并且能查看其中的局部变量最好了。
可惜的是sun提供的jdk并不能查看运行中的局部变量
- Oracle RAC Failover 详解
aijuans
oracle
Oracle RAC 同时具备HA(High Availiablity) 和LB(LoadBalance). 而其高可用性的基础就是Failover(故障转移). 它指集群中任何一个节点的故障都不会影响用户的使用,连接到故障节点的用户会被自动转移到健康节点,从用户感受而言, 是感觉不到这种切换。
Oracle 10g RAC 的Failover 可以分为3种:
1. Client-Si
- form表单提交数据编码方式及tomcat的接受编码方式
antonyup_2006
JavaScripttomcat浏览器互联网servlet
原帖地址:http://www.iteye.com/topic/266705
form有2中方法把数据提交给服务器,get和post,分别说下吧。
(一)get提交
1.首先说下客户端(浏览器)的form表单用get方法是如何将数据编码后提交给服务器端的吧。
对于get方法来说,都是把数据串联在请求的url后面作为参数,如:http://localhost:
- JS初学者必知的基础
百合不是茶
js函数js入门基础
JavaScript是网页的交互语言,实现网页的各种效果,
JavaScript 是世界上最流行的脚本语言。
JavaScript 是属于 web 的语言,它适用于 PC、笔记本电脑、平板电脑和移动电话。
JavaScript 被设计为向 HTML 页面增加交互性。
许多 HTML 开发者都不是程序员,但是 JavaScript 却拥有非常简单的语法。几乎每个人都有能力将小的
- iBatis的分页分析与详解
bijian1013
javaibatis
分页是操作数据库型系统常遇到的问题。分页实现方法很多,但效率的差异就很大了。iBatis是通过什么方式来实现这个分页的了。查看它的实现部分,发现返回的PaginatedList实际上是个接口,实现这个接口的是PaginatedDataList类的对象,查看PaginatedDataList类发现,每次翻页的时候最
- 精通Oracle10编程SQL(15)使用对象类型
bijian1013
oracle数据库plsql
/*
*使用对象类型
*/
--建立和使用简单对象类型
--对象类型包括对象类型规范和对象类型体两部分。
--建立和使用不包含任何方法的对象类型
CREATE OR REPLACE TYPE person_typ1 as OBJECT(
name varchar2(10),gender varchar2(4),birthdate date
);
drop type p
- 【Linux命令二】文本处理命令awk
bit1129
linux命令
awk是Linux用来进行文本处理的命令,在日常工作中,广泛应用于日志分析。awk是一门解释型编程语言,包含变量,数组,循环控制结构,条件控制结构等。它的语法采用类C语言的语法。
awk命令用来做什么?
1.awk适用于具有一定结构的文本行,对其中的列进行提取信息
2.awk可以把当前正在处理的文本行提交给Linux的其它命令处理,然后把直接结构返回给awk
3.awk实际工
- JAVA(ssh2框架)+Flex实现权限控制方案分析
白糖_
java
目前项目使用的是Struts2+Hibernate+Spring的架构模式,目前已经有一套针对SSH2的权限系统,运行良好。但是项目有了新需求:在目前系统的基础上使用Flex逐步取代JSP,在取代JSP过程中可能存在Flex与JSP并存的情况,所以权限系统需要进行修改。
【SSH2权限系统的实现机制】
权限控制分为页面和后台两块:不同类型用户的帐号分配的访问权限是不同的,用户使
- angular.forEach
boyitech
AngularJSAngularJS APIangular.forEach
angular.forEach 描述: 循环对obj对象的每个元素调用iterator, obj对象可以是一个Object或一个Array. Iterator函数调用方法: iterator(value, key, obj), 其中obj是被迭代对象,key是obj的property key或者是数组的index,value就是相应的值啦. (此函数不能够迭代继承的属性.)
- java-谷歌面试题-给定一个排序数组,如何构造一个二叉排序树
bylijinnan
二叉排序树
import java.util.LinkedList;
public class CreateBSTfromSortedArray {
/**
* 题目:给定一个排序数组,如何构造一个二叉排序树
* 递归
*/
public static void main(String[] args) {
int[] data = { 1, 2, 3, 4,
- action执行2次
Chen.H
JavaScriptjspXHTMLcssWebwork
xwork 写道 <action name="userTypeAction"
class="com.ekangcount.website.system.view.action.UserTypeAction">
<result name="ssss" type="dispatcher">
- [时空与能量]逆转时空需要消耗大量能源
comsci
能源
无论如何,人类始终都想摆脱时间和空间的限制....但是受到质量与能量关系的限制,我们人类在目前和今后很长一段时间内,都无法获得大量廉价的能源来进行时空跨越.....
在进行时空穿梭的实验中,消耗超大规模的能源是必然
- oracle的正则表达式(regular expression)详细介绍
daizj
oracle正则表达式
正则表达式是很多编程语言中都有的。可惜oracle8i、oracle9i中一直迟迟不肯加入,好在oracle10g中终于增加了期盼已久的正则表达式功能。你可以在oracle10g中使用正则表达式肆意地匹配你想匹配的任何字符串了。
正则表达式中常用到的元数据(metacharacter)如下:
^ 匹配字符串的开头位置。
$ 匹配支付传的结尾位置。
*
- 报表工具与报表性能的关系
datamachine
报表工具birt报表性能润乾报表
在选择报表工具时,性能一直是用户关心的指标,但是,报表工具的性能和整个报表系统的性能有多大关系呢?
要回答这个问题,首先要分析一下报表的处理过程包含哪些环节,哪些环节容易出现性能瓶颈,如何优化这些环节。
一、报表处理的一般过程分析
1、用户选择报表输入参数后,报表引擎会根据报表模板和输入参数来解析报表,并将数据计算和读取请求以SQL的方式发送给数据库。
2、
- 初一上学期难记忆单词背诵第一课
dcj3sjt126com
wordenglish
what 什么
your 你
name 名字
my 我的
am 是
one 一
two 二
three 三
four 四
five 五
class 班级,课
six 六
seven 七
eight 八
nince 九
ten 十
zero 零
how 怎样
old 老的
eleven 十一
twelve 十二
thirteen
- 我学过和准备学的各种技术
dcj3sjt126com
技术
语言VB https://msdn.microsoft.com/zh-cn/library/2x7h1hfk.aspxJava http://docs.oracle.com/javase/8/C# https://msdn.microsoft.com/library/vstudioPHP http://php.net/manual/en/Html
- struts2中token防止重复提交表单
蕃薯耀
重复提交表单struts2中token
struts2中token防止重复提交表单
>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>
蕃薯耀 2015年7月12日 11:52:32 星期日
ht
- 线性查找二维数组
hao3100590
二维数组
1.算法描述
有序(行有序,列有序,且每行从左至右递增,列从上至下递增)二维数组查找,要求复杂度O(n)
2.使用到的相关知识:
结构体定义和使用,二维数组传递(http://blog.csdn.net/yzhhmhm/article/details/2045816)
3.使用数组名传递
这个的不便之处很明显,一旦确定就是不能设置列值
//使
- spring security 3中推荐使用BCrypt算法加密密码
jackyrong
Spring Security
spring security 3中推荐使用BCrypt算法加密密码了,以前使用的是md5,
Md5PasswordEncoder 和 ShaPasswordEncoder,现在不推荐了,推荐用bcrpt
Bcrpt中的salt可以是随机的,比如:
int i = 0;
while (i < 10) {
String password = "1234
- 学习编程并不难,做到以下几点即可!
lampcy
javahtml编程语言
不论你是想自己设计游戏,还是开发iPhone或安卓手机上的应用,还是仅仅为了娱乐,学习编程语言都是一条必经之路。编程语言种类繁多,用途各 异,然而一旦掌握其中之一,其他的也就迎刃而解。作为初学者,你可能要先从Java或HTML开始学,一旦掌握了一门编程语言,你就发挥无穷的想象,开发 各种神奇的软件啦。
1、确定目标
学习编程语言既充满乐趣,又充满挑战。有些花费多年时间学习一门编程语言的大学生到
- 架构师之mysql----------------用group+inner join,left join ,right join 查重复数据(替代in)
nannan408
right join
1.前言。
如题。
2.代码
(1)单表查重复数据,根据a分组
SELECT m.a,m.b, INNER JOIN (select a,b,COUNT(*) AS rank FROM test.`A` A GROUP BY a HAVING rank>1 )k ON m.a=k.a
(2)多表查询 ,
使用改为le
- jQuery选择器小结 VS 节点查找(附css的一些东西)
Everyday都不同
jquerycssname选择器追加元素查找节点
最近做前端页面,频繁用到一些jQuery的选择器,所以特意来总结一下:
测试页面:
<html>
<head>
<script src="jquery-1.7.2.min.js"></script>
<script>
/*$(function() {
$(documen
- 关于EXT
tntxia
ext
ExtJS是一个很不错的Ajax框架,可以用来开发带有华丽外观的富客户端应用,使得我们的b/s应用更加具有活力及生命力。ExtJS是一个用 javascript编写,与后台技术无关的前端ajax框架。因此,可以把ExtJS用在.Net、Java、Php等各种开发语言开发的应用中。
ExtJs最开始基于YUI技术,由开发人员Jack
- 一个MIT计算机博士对数学的思考
xjnine
Math
在过去的一年中,我一直在数学的海洋中游荡,research进展不多,对于数学世界的阅历算是有了一些长进。为什么要深入数学的世界?作为计算机的学生,我没有任何企图要成为一个数学家。我学习数学的目的,是要想爬上巨人的肩膀,希望站在更高的高度,能把我自己研究的东西看得更深广一些。说起来,我在刚来这个学校的时候,并没有预料到我将会有一个深入数学的旅程。我的导师最初希望我去做的题目,是对appe