路径规划总结

路径规划论文总结

概述

路径规划在自动驾驶中占有比较重要的位置，一些路径的规划算法在自动驾驶的路径选择中比较关键。
一般来说，路径规划涉及路径搜索，避障以及产生可以保证舒适和效率的轨迹的生成。目前存在的论文也是对这些方面进行研究，主要涉及①寻路，②选择最安全的策略和③决定最可行的轨迹。
当然，V2V和V2I的研究也是路径规划中的一个比较重要的方向。
决策在自动驾驶中至关重要，他可以被很多算法实现。路径规划的目的在于寻找通往目的地的安全的道路。同时要考虑到车辆的动力学模型，策略以及道路交通规则和路边沿等。

概念和定义

现存的路径规划算法主要来源于移动机器人，在本文中主要阐述四个方面的算法：

• 路线规划 (route planning)
• 路径规划 (path planning)
• 策略选择
• 轨迹规划 也叫做控制规划（trajectory planning）
  路线规划(route planning)就是在给定起始点和目标点的前提下，结合当前实时的交通流信息规划出全局的道路路线。但是一般来说自动驾驶不会过多关注这一点，更多的关注路径、策略和轨迹规划。

路线规划是根据提供的起始点和目的地，以及结合道路信息和电子地图来进行全局的路线规划。关于路线规划，我也会具体详细的介绍，可以参看书籍The DARPA Urban Challenge。

下面就是一些概念的介绍,为了交流方面，我就不把一些英文名词翻译成中文。

Configuration space and State

在一个固定坐标系下定义一个车的位置和指向的特性向量，我们叫做 configuration vector，那么一系列的这样的configuration vector就形成了configuration space。

一个描述本车当前特性的集合被称为一个车在当前时刻的状态（State）,一般用来描述当前车的状态的量有position(x,y,z), orientation( θx,θy,θz ),线速度line velocity( vx,vy,vz )以及角速度angular velocity( ωx,ωy,ωz )。

一个车辆可以简化为一个简单的模型bicycle model，两个前轮和两个后轮都可以等效为自行车的前轮和后轮，这样一来，车辆的状态就可以简单的利用 (x,y,θ) 来描述, (x,y) 分别指代的是车辆重心的位置,而 θ 表示车辆的车头指向。这一假设的前提是内侧滑移、外侧滑移和方向盘转角是相等的。

关于完整可积分的定义：
如果一个机器人可以控制的关节变量数量等于机器人本身的自由度，那么这个机器人是完整可积分的，否则他就是非完整积分的。
Car-like robots按照bicycle model，他有三个自由度 (x,y,θ) ，但是本身可以控制的变量只有两个:
- 车辆可以按照本身当前指向的切线方向进行前进和后退。
- 车辆的转向角可以变化。
也就是说紧紧可以控制车辆的油门踏板、制动和方向盘转角。

Action

Action 是可以引起车辆状态改变的系统输入（比如说是加速度和方向盘转角）， Action Space 是一系列Action 的集合。

Path

Path 指的是从configuration space的起点和终点之间一个连续的序列。，也就是说它是一段从起点到终点，没有障碍物的一段几何轨迹。
Path-Planning 指的是由给定的起始点和末端点规划出一条可行的几何路径的过程，在这过程中需要考虑到路段和车道的边界，交通灯信息以及各种障碍物，比如行人、车辆和自行车俩等。

Manoeuvre(策略规划)

相对于位置和速度控制来说，Manoeuvre可以说是一种比较高层次的车辆运动描述。超车、換道、直行和转弯都是策略的一种。

Trajectory

Trajectory指的是一系列的车辆状态的集合，它是包含时间和速度的序列。
Trajectory Planning更多的是关于实时的规划一个车的当前状态到下一状态的过程，是整个path planning的结果更符合车辆运动学原理。

路径规划的搜索空间

对于路径规划来说，如果想要定量的去读取道路的信息，那么首先，需要将这些连续的路径信息转化为离散的、可以容易表达的数字路网。只有这样，我们才能够很好利用这些离散道路表达来进行路径的选取和规划。除此以外，将这些连续的道路信息进行离散化，也可以降低计算负载，提高规划的速度。

目前的现存的搜索空间表达方法有一下几种：
- Driving Corridors
- Voronoi Diagrams
- Lattices
- Occupancy Grids

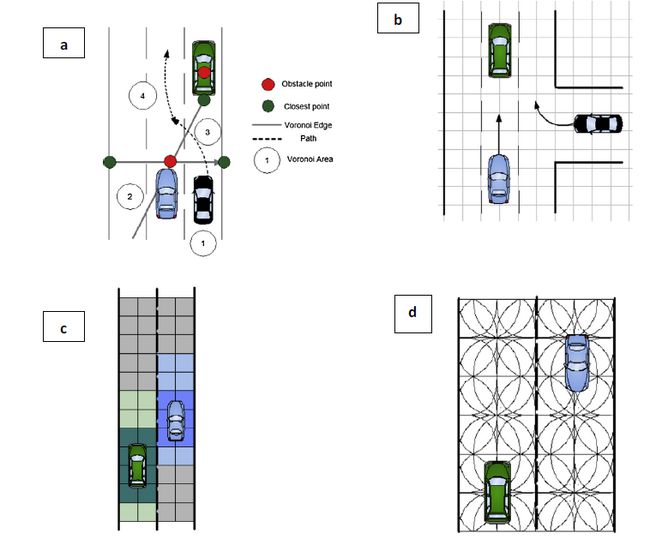
Voronoi Diagrams（图a）

Voronoi Diagrams可以在车辆和障碍点之间产生一条最大距离的路径。这一算法可以用在自动泊车的过程中，比较适用于静态环境中。有论文利用voronoi diagram结合人工势场法产生避障的路径。
但是这一算法来源于移动机器人，对于on-road path-planning 不是很适合，所以对于自动驾驶来说也不是很适用。

Occupancy Grids （图b）& Cost map （图c）

Occupancy Grids和Cost map比较相似，都是将空间划分成细小网格，然后将每一个网格和其被障碍物占的概率或者是网格的消耗关联起来。根据概率地图或者消耗地图进行路径规划。

State Lattices（图d）

State Lattices可以说是grid的一种变种，它是grid的一种泛化。grid是由方框和长方体不断堆砌的，而lattices是不断各种不同状态之间的路径堆砌而成。State Lattices算法克服了基于网格算法的效率的同时，没有偶额外增加计算负载。

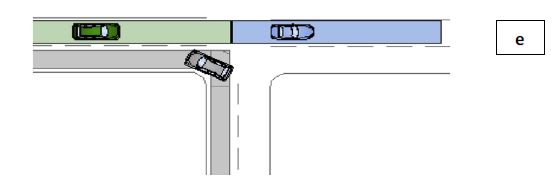
Driving Corridors

Driving Corridors是一段连续的无障碍的路段，这一路段的边界是道路和车道边界以及障碍点等。这些道路和车道边界信息可以由数字地图或者SLAM的方法获得。这些driving corridors的中线就是规划的路径。