动态规划及其在Apollo项目Planning模块的应用

严正声明：本文系作者davidhopper原创，未经许可，不得转载。

动态规划的英文为：Dynamic Programming，这里的“Programming”并非指编写程序代码，而是指一种表格计算法（a tabular method），即基于表格查询的方法计算得到最优结果，因此中文将其翻译成“动态规划”不甚严谨，当然有些垃圾文献将其翻译成“动态编程”就更是无稽之谈了。关于动态规划算法的原理，MIT出版的专著：“Introduction to Algorithms Third Edition (Thomas H. Cormen, Charles E. leiserson, Ronald L. Rivest, Clifford Stein)”（中文版《算法导论》好像是机械工业出版社翻译的，只要英文过得去，建议看原著较好）讲解得不错，本文的算法原理及示例均摘自该书。

一、动态规划算法原理及示例分析

1.1 基本原理

动态规划与分治法（the divide-and-conquer method）有些类似，也是将问题分解为多个子问题，并且基于子问题的结果获得最终解。二者的区别是，分治法将初始问题划分为多个不关联（disjoint）的子问题（subproblem)（即子问题互不依赖），递归地解决子问题，然后将子问题的解合并得到初始问题的解。与之相反，动态规划法分解得到的子问题是相互重叠的（overlap），即子问题依赖于子子问题（subsubproblem)，子子问题又进一步依赖于下一级的子子问题，这样不断循环直至抵达不需分解的初始条件。在求解过程中，为了避免重复计算子子问题从而提高算法效率，需要将一系列子子问题的解保存到一张表中（table，C++编程一般使用std::array、std::vector或std::list实现），这也就是动态规划又被称为查表计算法的原因。
动态规划一般应用于最优化问题（optimization problems）。这类问题一般存在多个解，每个解都具有一个度量值，我们期望得到具有度量值最优（即取最大或最小值）的解。该最优解一般称为最优化问题的一个解。注意，这个解并非唯一，因为最优化问题可能存在多个最优解。
构建一个动态规划算法的一般步骤如下：

1. 刻画出一个最优解的结构特征（即使用数学表达式来表述一个最优解）；
2. 迭代定义一个最优解的度量值；
3. 计算每个最优解的度量值，通常采用自下而上的方式；
4. 根据计算得到的信息构建出原问题的一个最优解。

步骤1-3是使用动态规划求解问题的基础形式。如果我们只需获得最优解的度量值而非最优解本身，则可以忽略步骤4。以上描述较为抽象，下面以“Introduction to Algorithms ”书中提到的钢管切割（rod cutting）问题为例，对动态规划的求解过程进行描述。

1.2 钢管切割问题的动态规划求解过程

1.2.1 问题描述
给定钢管长度$i$（$i=1,2,...,n$, 单位：英寸）和对应价格$p_i$（单位：美元）的描述表，求解让长度为$n$的钢管获得最大收益（revenue）的切割方法。$n=10$的描述表如下：

长度$i$	1	2	3	4	5	6	7	8	9	10
价格$p_i$	1	5	8	9	10	17	17	20	24	30

钢管长度为4时的所有切割方式如下图所示（图片来源于“Introduction to Algorithms ”）：

根据上图，显然最优切割方案是( c )，即将长度为4的钢管切割为2根长度为2的钢管，最大收益值为10。
1.2.2 数学表达式
设一个最优切割将长度为$n$的钢管切割为$k$份（$1\le k\le n$），则最优切割的数学描述为：
$$n=i_1+i_2+...+i_k$$
式中，$i_1,i_2,...,i_k$分别表示第$1,2,...,k$次切割长度。该切割提供的最大收益则可表示为：
$$r_n=p_{i_1}+p_{i_2}+...+p_{i_k}$$
对于表中描述的$n=10$的切割问题，我们可逐级求得长度为$1,2,...,10$的最大收益及最估切割方案：
$$n=1,最大收益：r_1=1,最优解为：1=1（不切割）$$
$$n=2,最大收益：r_2=5,最优解为：2=2（不切割）$$
$$n=3,最大收益：r_3=8,最优解为：3=3（不切割）$$
$$n=4,最大收益：r_4=10,最优解为：4=2+2$$
$$n=5,最大收益：r_5=13,最优解为：5=2+3$$
$$n=6,最大收益：r_6=17,最优解为：6=6（不切割）$$
$$n=7,最大收益：r_7=18,最优解为：7=1+6或7=2+2+3$$
$$n=8,最大收益：r_8=22,最优解为：8=2+6$$
$$n=9,最大收益：r_9=25,最优解为：9=3+6$$
$$n=10,最大收益：r_{10}=30,最优解为：10=10（不切割）$$
一般地，我们可以将最优切割问题描述为：长度$n\ge 1$的钢管，其最大切割收益$r_n$依赖于长度更短的钢管切割收益：
$$r_n=max(p_n,r_1+r_{n-1},r_2+r_{n-2},...,r_{n-1}+r_1)$$
若记$r_0=0$，则可将上式写为更简洁的形式：
$$r_n=\underset{1\le i\le n}{\max }(p_i+r_{n-i})$$
1.2.3 算法伪代码
a) 自上而下的迭代算法

CUT-ROD(p, n)	
	if n == 0
		return 0
	q = -1
	for i = 1 to n				
			q = max(q, p[i] + CUT-ROD(p, n-i))			
	return q

上述迭代算法是对钢管切割问题数学表达式的直接翻译，虽然代码看上去直接、简单，但算法效率非常低，时间复杂度为$O(2^n)$，并且在求解得到最大收益后，难以同时获得最优切割方案。
b) 自下而上的二次规划算法

BOTTOM-UP-CUT-ROD(p, n)
	let r[0, ..., n] be a new array of maximum revenues
	let s[0, ..., n] be a new array of the optimal size of the first piece to cut off
	r[0] = 0	
	for j = 1 to n
		q = -1
		for i = 1 to j	
			if q < p[i] + r[j-i]	
				q = p[i] + r[j-i]
				s[j] = i
		r[j] = q
	return r and s

注意动态规划算法使用一个收益数组将不同长度钢管的最大收益值全部存储下来，避免多次计算，因此算法效率得以提高，时间复杂度为$O(n^2)$，并且易于求解最优分割方案。
c) 输出最优分割方案

PRINT-CUT-ROD-SOLUTION(p, n)	
	(r, s) = BOTTOM-UP-CUT-ROD(p, n)
	while n > 0
		print s[n]
		n = n - s[n]

1.2.4 算法的C++实现
采用C++ 14标准实现算法，代码如下：

// David Hopper
// 2018-2-27
// [email protected]

#include 
#include 
#include 
#include 
#include 

constexpr std::array<int, 10> kPrice = {1, 5, 8, 9, 10, 17, 17, 20, 24, 30};

// A top-down recursive rod cutting algorithm.
// Time complexity is O(2^n).
template <class ConstIter>
int recursive_rod_cutting(ConstIter first, ConstIter last);
int recursive_rod_cutting(const int *const price, int n);

// A bottom-up dynamic programming rod cutting algorithm.
// Time complexity is O(n^2).
template <class ConstIter>
int dynamic_programming_rod_cutting(ConstIter first, ConstIter last,
                                    std::vector<int> &max_revenues,
                                    std::vector<int> &first_cutting_pieces);
int dynamic_programming_rod_cutting(const int *const price, int n,
                                    std::vector<int> &max_revenues,
                                    std::vector<int> &first_cutting_pieces);

// Print the optimal rod cutting scheme.
void print_rod_cutting_solution(const std::vector<int> &first_cutting_pieces,
                                int n);

int main(int argc, char **argv) {
  int num = 10;
  if (argc > 1) {
    std::istringstream is(argv[1]);
    is >> num;
    if (num <= 0) {
      std::cout << "The minimum length should be larger than 0. " << std::endl;
      std::cout << "The current length is set to 1" << std::endl;
      num = 1;
    }
    if (num > 10) {
      std::cout << "The maxium length should be smaller than 10. " << std::endl;
      std::cout << "The current length is set to 10" << std::endl;
      num = 10;
    }
  }

  auto t1 = std::chrono::system_clock::now();
  // int max_revenue = recursive_rod_cutting(kPrice.data(), num);
  int max_revenue =
      recursive_rod_cutting(kPrice.begin(), std::next(kPrice.begin(), num));
  auto t2 = std::chrono::system_clock::now();
  std::cout << "The maxium revenue of a " << num << " inch rod_cutting problem "
            << "with recrusive method is: " << max_revenue << std::endl;
  std::cout
      << "Elapsed time in microseconds is: "
      << std::chrono::duration_cast<std::chrono::microseconds>(t2 - t1).count()
      << std::endl;

  t1 = std::chrono::system_clock::now();
  std::vector<int> max_revenues(num + 1, 0);
  std::vector<int> first_cutting_pieces(num + 1, 0);
  // max_revenue = dynamic_programming_rod_cutting(kPrice.data(),
  //                                               num,
  //                                               max_revenues,
  //                                               first_cutting_pieces);
  max_revenue = dynamic_programming_rod_cutting(
      kPrice.begin(), std::next(kPrice.begin(), num), max_revenues,
      first_cutting_pieces);
  t2 = std::chrono::system_clock::now();
  std::cout << "The maxium revenue of a " << num << " inch rod_cutting problem "
            << "with dynamic programming method is: " << max_revenue
            << std::endl;
  std::cout
      << "Elapsed time in microseconds is: "
      << std::chrono::duration_cast<std::chrono::microseconds>(t2 - t1).count()
      << std::endl;

  std::cout << "max_revenues are: " << std::endl;
  for (int i = 0; i < num + 1; ++i) {
    std::cout << max_revenues[i] << ",";
  }
  std::cout << std::endl;
  std::cout << "first_cutting_pieces are: " << std::endl;
  for (int i = 0; i < num + 1; ++i) {
    std::cout << first_cutting_pieces[i] << ",";
  }
  std::cout << std::endl;

  print_rod_cutting_solution(first_cutting_pieces, num);

  return 0;
}

// A top-down recursive rod cutting algorithm.
// Time complexity is O(2^n).
template <class ConstIter>
int recursive_rod_cutting(ConstIter first, ConstIter last) {
  int n = std::distance(first, last);
  if (n <= 0) {
    return 0;
  }
  int max_revenue = -1;
  for (int i = 0; i < n; ++i) {
    ConstIter temp_last = std::next(first, n - i - 1);
    max_revenue =
        std::max(max_revenue, *(std::next(first, i)) +
                                  recursive_rod_cutting(first, temp_last));
  }
  // std::cout << "The maxium revenue in recursive_rod_cutting(price, " < < n <<
  // ")"
  //          << " is: " << max_revenue << std::endl;
  return max_revenue;
}

// A top-down recursive rod cutting algorithm.
// Time complexity is O(2^n).
int recursive_rod_cutting(const int *const price, int n) {
  if (n <= 0) {
    return 0;
  }
  int max_revenue = -1;
  for (int i = 0; i < n; ++i) {
    max_revenue = std::max(max_revenue,
                           price[i] + recursive_rod_cutting(price, n - i - 1));
  }
  // std::cout << "The maxium revenue in recursive_rod_cutting(price, " << n <<
  // ")"
  //          << " is: " << max_revenue << std::endl;
  return max_revenue;
}

// A bottom-up dynamic programming rod cutting algorithm.
// Time complexity is O(n^2).
template <class ConstIter>
int dynamic_programming_rod_cutting(ConstIter first, ConstIter last,
                                    std::vector<int> &max_revenues,
                                    std::vector<int> &first_cutting_pieces) {
  int n = std::distance(first, last);
  if (static_cast<int>(max_revenues.size()) < (n + 1) ||
      static_cast<int>(first_cutting_pieces.size()) < (n + 1)) {
    return 0;
  }

  for (int j = 1; j < n + 1; ++j) {
    int max_revenue = -1;
    for (int i = 0; i < j; ++i) {
      int prev_max_revenue = *std::next(first, i) + max_revenues[j - i - 1];
      if (max_revenue < prev_max_revenue) {
        max_revenue = prev_max_revenue;
        first_cutting_pieces[j] = i + 1;
      }
    }
    // std::cout << "The maxium revenue in dynamic_programming_rod_cutting() for
    // loop "
    //          << j << " is: " << max_revenue << std::endl;
    max_revenues[j] = max_revenue;
  }

  return max_revenues[n];
}

// A bottom-up dynamic programming rod cutting algorithm.
// Time complexity is O(n^2).
int dynamic_programming_rod_cutting(const int *const price, int n,
                                    std::vector<int> &max_revenues,
                                    std::vector<int> &first_cutting_pieces) {
  if (static_cast<int>(max_revenues.size()) < (n + 1) ||
      static_cast<int>(first_cutting_pieces.size()) < (n + 1)) {
    return 0;
  }

  for (int j = 1; j < n + 1; ++j) {
    int max_revenue = -1;
    for (int i = 0; i < j; ++i) {
      int prev_max_revenue = price[i] + max_revenues[j - i - 1];
      if (max_revenue < prev_max_revenue) {
        max_revenue = prev_max_revenue;
        first_cutting_pieces[j] = i + 1;
      }
    }
    // std::cout << "The maxium revenue in dynamic_programming_rod_cutting() for
    // loop "
    //          << j << " is: " << max_revenue << std::endl;
    max_revenues[j] = max_revenue;
  }

  return max_revenues[n];
}

void print_rod_cutting_solution(const std::vector<int> &first_cutting_pieces,
                                int n) {
  if (n >= static_cast<int>(first_cutting_pieces.size())) {
    return;
  }
  std::cout << "The optimal cutting scheme is: " << std::endl;
  int prev_n = n;
  while (n > 0) {
    std::cout << first_cutting_pieces[n] << " -> ";
    n -= first_cutting_pieces[n];
    // avoid infinite loop if there is something wrong in first_cutting_pieces.
    if (n >= prev_n) {
      break;
    }
    prev_n = n;
  }
  std::cout << "end. " << std::endl;
}

在Linux系统中的编译命令如下：

g++ -g -Wall -std=c++14  *.cpp -o rot_cutting

使用CMake编译的配置文件CMakeLists.txt内容如下：

cmake_minimum_required(VERSION 3.0)
project(rod_cutting)

set(CMAKE_CXX_STANDARD 14)
set(SOURCE main.cpp)
add_executable(${PROJECT_NAME} ${SOURCE})

./rod_cutting 5的运行结果如下：

The maxium revenue of a 5 inch rod_cutting problem with recrusive method is: 13
Elapsed time in microseconds is: 5
The maxium revenue of a 5 inch rod_cutting problem with dynamic programming method is: 13
Elapsed time in microseconds is: 9
max_revenues are:
0,1,5,8,10,13,
first_cutting_pieces are:
0,1,2,3,2,2,
The optimal cutting scheme is:
2 -> 3 -> end.

./rod_cutting 8的运行结果如下：

The maxium revenue of a 8 inch rod_cutting problem with recrusive method is: 22
Elapsed time in microseconds is: 25
The maxium revenue of a 8 inch rod_cutting problem with dynamic programming method is: 22
Elapsed time in microseconds is: 12
max_revenues are:
0,1,5,8,10,13,17,18,22,
first_cutting_pieces are:
0,1,2,3,2,2,6,1,2,
The optimal cutting scheme is:
2 -> 6 -> end.

./rod_cutting 10的运行结果如下：

The maxium revenue of a 10 inch rod_cutting problem with recrusive method is: 30
Elapsed time in microseconds is: 56
The maxium revenue of a 10 inch rod_cutting problem with dynamic programming method is: 30
Elapsed time in microseconds is: 12
max_revenues are:
0,1,5,8,10,13,17,18,22,25,30,
first_cutting_pieces are:
0,1,2,3,2,2,6,1,2,3,10,
The optimal cutting scheme is:
10 -> end.

二、动态规划在Apollo项目Planning模块的应用

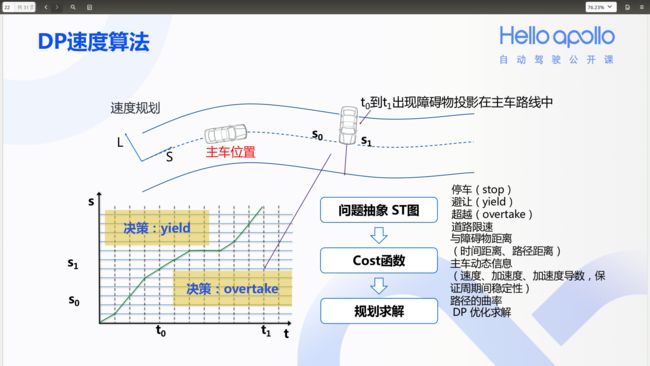
Apollo项目Planning模块的EMPlanner中使用动态规划生成代价（cost）最小的多项式路径（DP路径，见Apollo项目中的DPRoadGraph类）和速度（DP速度，见Apollo项目中的DpStGraph类），DP路径算法和DP速度算法的示意性描述如下图所示（来自百度Apollo项目公开课PPT）：


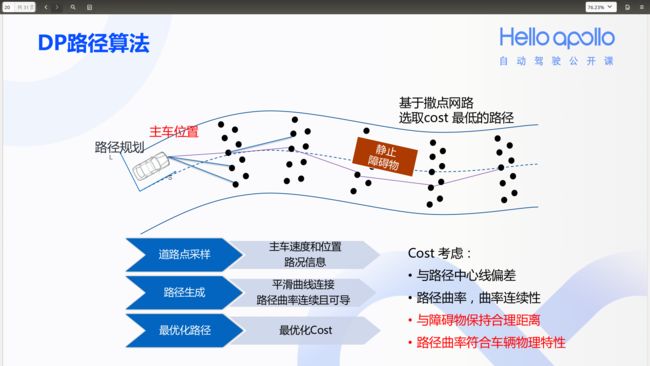
DP路径算法的基本思路是，基于给定的一条中心路径（称为参考线，ReferenceLine）和车道边界条件，每隔一定间隔的纵向距离（称为不同级（level）上的s值）对道路截面进行均匀采样（与中心点的横向偏移值称为为l值），这样会得到图中黑点所示的采样点（这些采样点称为航点，waypoint）数组。基于一定的规则，可以给出各航点迁移的代价值（cost）。航点迁移不一定需要逐级进行，可以从第一级跳到第三级甚至终点，只要迁移代价值最小化即可，这显然满足动态规划的求解思路。
DP速度算法的基本思路是，在DP路径算法生成一条可行驶的路径后，从起点开始，考虑避开路径中的所有障碍物，并且让加减速最为平顺，以最优的速度曲线（即t-s平面中的绿色曲线）安全抵达终点，这也可以使用动态规划的思路求解。

DP路径算法的代码注释

航点数组生成

// 采样获得路径航点
bool DPRoadGraph::SamplePathWaypoints(
    const common::TrajectoryPoint &init_point,
    std::vector<std::vector<common::SLPoint>> *const points) {
  CHECK_NOTNULL(points);

  // 最小采样距离
  const double kMinSampleDistance = 40.0;
  // 总长度 = min(初始点 + max(初始速度 × 8, 最小采样距离), 参考线长度）
  const double total_length = std::fmin(
      init_sl_point_.s() + std::fmax(init_point.v() * 8.0, kMinSampleDistance),
      reference_line_.Length());

  // 采样前视时长
  constexpr double kSamplePointLookForwardTime = 4.0;We can just use `sl = common::util::MakeSLPoint(s, l);` . 
  // 采样步长 = 初始速度 × 采样前视时长，要求：
  // step_length_min(默认值：8) <= 采样步长 <= step_length_max(默认值：15)
  const double level_distance =
      common::math::Clamp(init_point.v() * kSamplePointLookForwardTime,
                          config_.step_length_min(), config_.step_length_max());
  // 累计轨迹弧长
  double accumulated_s = init_sl_point_.s();
  // 上次轨迹弧长
  double prev_s = accumulated_s;
  // 累计轨迹弧长小于总长度时，将累计轨迹弧长每次加上采样步长，进行循环采样
  for (std::size_t i = 0; accumulated_s < total_length; ++i) {
    accumulated_s += level_distance;
    if (accumulated_s + level_distance / 2.0 > total_length) {
      accumulated_s = total_length;
    }
    // 本次轨迹弧长：取累计轨迹弧长与总长度之间的最小值
    const double s = std::fmin(accumulated_s, total_length);
    // 最小允许采样步长
    constexpr double kMinAllowedSampleStep = 1.0;
    // 若本次轨迹弧长与上次轨迹弧长间的差值小于最小允许采样步长，跳过本次采样
    if (std::fabs(s - prev_s) < kMinAllowedSampleStep) {
      continue;
    }
    prev_s = s;

    // 左车道宽
    double left_width = 0.0;
    // 右车道宽
    double right_width = 0.0;
    reference_line_.GetLaneWidth(s, &left_width, &right_width);

    // 边界缓冲
    constexpr double kBoundaryBuff = 0.20;
    const auto &vehicle_config =
        common::VehicleConfigHelper::instance()->GetConfig();
    const double half_adc_width = vehicle_config.vehicle_param().width() / 2.0;
    // 右侧允许宽度 = 右车道宽 - 半车宽 - 边界缓冲
    const double eff_right_width = right_width - half_adc_width - kBoundaryBuff;
    // 左侧允许宽度 = 左车道宽 - 半车宽 - 边界缓冲
    const double eff_left_width = left_width - half_adc_width - kBoundaryBuff;
    // 每步采样点数
    const size_t num_sample_per_level =
        FLAGS_use_navigation_mode ? config_.navigator_sample_num_each_level()
                                  : config_.sample_points_num_each_level();
    // 默认横向采样间隔
    double kDefaultUnitL = 1.2 / (num_sample_per_level - 1);
    if (reference_line_info_.IsChangeLanePath() && !IsSafeForLaneChange()) {
      kDefaultUnitL = 1.0;
    }
    // 横向采样距离
    const double sample_l_range = kDefaultUnitL * (num_sample_per_level - 1);
    // 右采样边界（车辆右侧为负值）
    double sample_right_boundary = -eff_right_width;
    // 左采样边界（车辆左侧为正值）
    double sample_left_boundary = eff_left_width;
    // 参考线正在改变车道时
    if (reference_line_info_.IsChangeLanePath()) {
      // 右采样边界取右采样边界与初始点横向偏移之间的最小值
      sample_right_boundary = std::fmin(-eff_right_width, init_sl_point_.l());
      // 左采样边界取左采样边界与初始点横向偏移之间的最大值
      sample_left_boundary = std::fmax(eff_left_width, init_sl_point_.l());

      // 若初始点横向偏移 > 左侧允许宽度，则将右侧采样边界设置为右侧采样边界与（初始点横向偏移
      // - 横向采样距离）之间的最大值
      if (init_sl_point_.l() > eff_left_width) {
        sample_right_boundary = std::fmax(sample_right_boundary,
                                          init_sl_point_.l() - sample_l_range);
      }
      // 若初始点横向偏移 < 右侧允许宽度，则将左侧采样边界设置为左侧采样边界与（初始点横向偏移
      // + 横向采样距离）之间的最小值
      if (init_sl_point_.l() < eff_right_width) {
        sample_left_boundary = std::fmin(sample_left_boundary,
                                         init_sl_point_.l() + sample_l_range);
      }
    }

    // 横向采样距离数组
    std::vector<double> sample_l;
    // 参考线正在改变车道且改变车道不安全时，将当前参考线到其他参考线的偏移值存储到横向采样距离数组
    if (reference_line_info_.IsChangeLanePath() && !IsSafeForLaneChange()) {
      sample_l.push_back(reference_line_info_.OffsetToOtherReferenceLine());
    } else {
      // 其他情形，从右采样边界到左采样边界，按照每步采样点数进行均匀采样，并将结果存储到横向采样距离数组
      common::util::uniform_slice(sample_right_boundary, sample_left_boundary,
                                  num_sample_per_level - 1, &sample_l);
      if (HasSidepass()) {
        // currently only left nudge is supported. Need road hard boundary for
        // both sides
        sample_l.clear();
        switch (sidepass_.type()) {
          case ObjectSidePass::LEFT: {
            // 左侧绕行：将（左侧允许宽度 + 左侧绕行距离）存储到横向采样距离数组
            sample_l.push_back(eff_left_width + config_.sidepass_distance());
            break;
          }
          case ObjectSidePass::RIGHT: {
            // 右侧绕行：将-（右侧允许宽度 + 右侧绕行距离）存储到横向采样距离数组
            sample_l.push_back(-eff_right_width - config_.sidepass_distance());
            break;
          }
          default:
            break;
        }
      }
    }
    // 本次采样点数组
    std::vector<common::SLPoint> level_points;
    planning_internal::SampleLayerDebug sample_layer_debug;
    for (size_t j = 0; j < sample_l.size(); ++j) {
      // 横向偏移值
      const double l = sample_l[j];
      constexpr double kResonateDistance = 1e-3;
      common::SLPoint sl;
      // 若为奇数采样点或者（总长度 - 累计轨迹弧长）几乎为0即已抵达采样终点，
      // 则直接将当前采样点坐标设置为(s, l)
      if (j % 2 == 0 ||
          total_length - accumulated_s < 2.0 * kResonateDistance) {
        sl = common::util::MakeSLPoint(s, l);
      } else {
        // 其他情形，将当前采样点坐标设置为（min(总长度，s+误差)，l）
        sl = common::util::MakeSLPoint(
            std::fmin(total_length, s + kResonateDistance), l);
      }
      sample_layer_debug.add_sl_point()->CopyFrom(sl);
      // 将当前采样点坐标存储到本次采样点数组
      level_points.push_back(std::move(sl));
    }
    // 若参考线未改变车道且不绕行，则将横向偏移值为0的采样点（即沿参考线方向的采样点）也加入本次采样点数组
    if (!reference_line_info_.IsChangeLanePath() && !HasSidepass()) {
      auto sl_zero = common::util::MakeSLPoint(s, 0.0);
      sample_layer_debug.add_sl_point()->CopyFrom(sl_zero);
      level_points.push_back(sl_zero);
    }

    if (!level_points.empty()) {
      planning_debug_->mutable_planning_data()
          ->mutable_dp_poly_graph()
          ->add_sample_layer()
          ->CopyFrom(sample_layer_debug);
      // 将本次的所有采样点存储到总采样点数组
      points->emplace_back(level_points);
    }
  }
  return true;
}

基于航点数组使用动态规划算法求解代价值最小的路径

bool DPRoadGraph::GenerateMinCostPath(
    const std::vector<const PathObstacle *> &obstacles,
    std::vector<DPRoadGraphNode> *min_cost_path) {
  CHECK(min_cost_path != nullptr);

  // 基于当前参考线及初始点，生成候选路径采样点数组
  // 路径航点（path_waypoints）里面的每个vecotr存储相同s值（轨迹累计弧长）下的多个采样点
  std::vector<std::vector<common::SLPoint>> path_waypoints;
  if (!SamplePathWaypoints(init_point_, &path_waypoints) ||
      path_waypoints.size() < 1) {
    AERROR << "Fail to sample path waypoints! reference_line_length = "
           << reference_line_.Length();
    return false;
  }
  // 将初始点加入到路径航点数组的最前面
  path_waypoints.insert(path_waypoints.begin(),
                        std::vector<common::SLPoint>{init_sl_point_});
  if (path_waypoints.size() < 2) {
    AERROR << "Too few path_waypoints.";
    return false;
  }

  // 输出路径航点调试信息
  for (uint32_t i = 0; i < path_waypoints.size(); ++i) {
    const auto &level_waypoints = path_waypoints.at(i);
    for (uint32_t j = 0; j < level_waypoints.size(); ++j) {
      ADEBUG << "level[" << i << "], "
             << level_waypoints.at(j).ShortDebugString();
    }
  }

  // 读取车辆配置信息
  const auto &vehicle_config =
      common::VehicleConfigHelper::instance()->GetConfig();

  // 轨迹代价
  TrajectoryCost trajectory_cost(
      config_, reference_line_, reference_line_info_.IsChangeLanePath(),
      obstacles, vehicle_config.vehicle_param(), speed_data_, init_sl_point_);

  // 最小代价值路图节表点链表
  std::list<std::list<DPRoadGraphNode>> graph_nodes;
  graph_nodes.emplace_back();
  graph_nodes.back().emplace_back(init_sl_point_, nullptr, ComparableCost());
  auto &front = graph_nodes.front().front();
  size_t total_level = path_waypoints.size();
  // 采用自下而上的动态规划算法，迭代更新最小代价值
  // graph_nodes存储的就是各级（level）路径航点（path_waypoints）所包含的最小代价航点
  // graph_nodes.back()（即最后一条航点链表）就是我们所需的最小代价航点链表
  for (std::size_t level = 1; level < path_waypoints.size(); ++level) {
    const auto &prev_dp_nodes = graph_nodes.back();
    const auto &level_points = path_waypoints[level];

    graph_nodes.emplace_back();

    for (size_t i = 0; i < level_points.size(); ++i) {
      const auto &cur_point = level_points[i];

      graph_nodes.back().emplace_back(cur_point, nullptr);
      auto &cur_node = graph_nodes.back().back();
      // 采用多线程并行计算最小代价值航点
      if (FLAGS_enable_multi_thread_in_dp_poly_path) {
        PlanningThreadPool::instance()->Push(std::bind(
            &DPRoadGraph::UpdateNode, this, std::ref(prev_dp_nodes), level,
            total_level, &trajectory_cost, &(front), &(cur_node)));

      } else {
        // 采用单线程计算最小代价值航点
        UpdateNode(prev_dp_nodes, level, total_level, &trajectory_cost, &front,
                   &cur_node);
      }
    }
    // 多线程模式下的同步
    if (FLAGS_enable_multi_thread_in_dp_poly_path) {
      PlanningThreadPool::instance()->Synchronize();
    }
  }

  // graph_nodes.back()（即最后一条航点链表）就是我们所需的最小代价航点链表
  // find best path
  DPRoadGraphNode fake_head;
  for (const auto &cur_dp_node : graph_nodes.back()) {
    fake_head.UpdateCost(&cur_dp_node, cur_dp_node.min_cost_curve,
                         cur_dp_node.min_cost);
  }

  // 从终点顺藤摸瓜向起点逐个找出最小代价值航点，并将其加入min_cost_path
  const auto *min_cost_node = &fake_head;
  while (min_cost_node->min_cost_prev_node) {
    min_cost_node = min_cost_node->min_cost_prev_node;
    min_cost_path->push_back(*min_cost_node);
  }
  if (min_cost_node != &graph_nodes.front().front()) {
    return false;
  }

  // 将航点顺序调整为起点到终点
  std::reverse(min_cost_path->begin(), min_cost_path->end());

  for (const auto &node : *min_cost_path) {
    ADEBUG << "min_cost_path: " << node.sl_point.ShortDebugString();
    planning_debug_->mutable_planning_data()
        ->mutable_dp_poly_graph()
        ->add_min_cost_point()
        ->CopyFrom(node.sl_point);
  }
  return true;
}

// 在当前level下，获得一条代价值最小的航点链表
void DPRoadGraph::UpdateNode(const std::list<DPRoadGraphNode> &prev_nodes,
                             const uint32_t level, const uint32_t total_level,
                             TrajectoryCost *trajectory_cost,
                             DPRoadGraphNode *front,
                             DPRoadGraphNode *cur_node) {
  DCHECK_NOTNULL(trajectory_cost);
  DCHECK_NOTNULL(front);
  DCHECK_NOTNULL(cur_node);
  for (const auto &prev_dp_node : prev_nodes) {
    const auto &prev_sl_point = prev_dp_node.sl_point;
    const auto &cur_point = cur_node->sl_point;
    double init_dl = 0.0;
    double init_ddl = 0.0;
    if (level == 1) {
      init_dl = init_frenet_frame_point_.dl();
      init_ddl = init_frenet_frame_point_.ddl();
    }
    // 生成当前点到前一level所有航点的的曲线
    QuinticPolynomialCurve1d curve(prev_sl_point.l(), init_dl, init_ddl,
                                   cur_point.l(), 0.0, 0.0,
                                   cur_point.s() - prev_sl_point.s());

    if (!IsValidCurve(curve)) {
      continue;
    }
    const auto cost =
        trajectory_cost->Calculate(curve, prev_sl_point.s(), cur_point.s(),
                                   level, total_level) +
        prev_dp_node.min_cost;
    // 根据代价最小的原则，在前一level所有航点中找到与当前点连接代价最小的航点，
    // 将结果存储于prev_dp_node中
    cur_node->UpdateCost(&prev_dp_node, curve, cost);

    // 尝试将当前点直接连接到初始点，看其代价是否比当前点到前一level航点的最小代价还小，
    // 若小于则将最小代价航点更新。这种情况一般只会存在于改变车道的情形。
    // try to connect the current point with the first point directly
    // only do this at lane change
    if (level >= 2) {
      init_dl = init_frenet_frame_point_.dl();
      init_ddl = init_frenet_frame_point_.ddl();
      QuinticPolynomialCurve1d curve(init_sl_point_.l(), init_dl, init_ddl,
                                     cur_point.l(), 0.0, 0.0,
                                     cur_point.s() - init_sl_point_.s());
      if (!IsValidCurve(curve)) {
        continue;
      }
      const auto cost = trajectory_cost->Calculate(
          curve, init_sl_point_.s(), cur_point.s(), level, total_level);
      cur_node->UpdateCost(front, curve, cost);
    }
  }
}

DP速度算法的代码注释

// 从st图中寻找代价值最小的速度曲线
// s：行驶距离，纵坐标；
// t：行驶时间，横坐标
// SpeedData* const speed_data表示speed_data本身（即指针自身）不能被修改，
// 但speed_data指向的内容可被修改，该函数就是通过它返回最优速度数据的。
Status DpStGraph::Search(SpeedData* const speed_data) {
  constexpr double kBounadryEpsilon = 1e-2;
  // 对边界条件进行初步筛选
  for (const auto& boundary : st_graph_data_.st_boundaries()) {
    // 若边界类型为禁停区，直接跳过
    if (boundary->boundary_type() == StBoundary::BoundaryType::KEEP_CLEAR) {
      continue;
    }
    // 若边界位于(0.0, 0.0)（即起始位置）或者边界的min_t和min_s比边界最小分辨率
    // kBounadryEpsilon还小，则将速度点的s值设为0.0，t值均匀采样递增。
    if (boundary->IsPointInBoundary({0.0, 0.0}) ||
        (std::fabs(boundary->min_t()) < kBounadryEpsilon &&
         std::fabs(boundary->min_s()) < kBounadryEpsilon)) {
      std::vector<SpeedPoint> speed_profile;
      double t = 0.0;
      for (int i = 0; i < dp_st_speed_config_.matrix_dimension_t();
           ++i, t += unit_t_) {
        SpeedPoint speed_point;
        speed_point.set_s(0.0);
        speed_point.set_t(t);
        speed_profile.emplace_back(speed_point);
      }
      speed_data->set_speed_vector(speed_profile);
      return Status::OK();
    }
  }

  // 若st图数据的边界条件为空，意味着前方没有障碍物，匀速前进即可。
  // speed_profile[i] = (0.0 + i * unit_s_, 0.0 + i * unit_t_);
  if (st_graph_data_.st_boundaries().empty()) {
    ADEBUG << "No path obstacles, dp_st_graph output default speed profile.";
    std::vector<SpeedPoint> speed_profile;
    double s = 0.0;
    double t = 0.0;
    for (int i = 0; i < dp_st_speed_config_.matrix_dimension_t() &&
                    i < dp_st_speed_config_.matrix_dimension_s();
         ++i, t += unit_t_, s += unit_s_) {
      SpeedPoint speed_point;
      speed_point.set_s(s);
      speed_point.set_t(t);
      speed_profile.emplace_back(speed_point);
    }
    speed_data->set_speed_vector(speed_profile);
    return Status::OK();
  }

  // 初始化代价表cost_table_
  if (!InitCostTable().ok()) {
    const std::string msg = "Initialize cost table failed.";
    AERROR << msg;
    return Status(ErrorCode::PLANNING_ERROR, msg);
  }
  // 计算代价表cost_table_中所有节点的总代价
  if (!CalculateTotalCost().ok()) {
    const std::string msg = "Calculate total cost failed.";
    AERROR << msg;
    return Status(ErrorCode::PLANNING_ERROR, msg);
  }
  // 通过计算得到的代价表cost_table_中所有节点的总代价，获取速度数据
  if (!RetrieveSpeedProfile(speed_data).ok()) {
    const std::string msg = "Retrieve best speed profile failed.";
    AERROR << msg;
    return Status(ErrorCode::PLANNING_ERROR, msg);
  }
  return Status::OK();
}

// 初始化代价表
Status DpStGraph::InitCostTable() {
  // 从配置文件读取s和t的维数
  uint32_t dim_s = dp_st_speed_config_.matrix_dimension_s();
  uint32_t dim_t = dp_st_speed_config_.matrix_dimension_t();
  // 维数检查，要求大于2
  DCHECK_GT(dim_s, 2);
  DCHECK_GT(dim_t, 2);
  // 生成代价表cost_table_，列为dim_t，行为dim_s，所有节点均初始化为：StGraphPoint()
  cost_table_ = std::vector<std::vector<StGraphPoint>>(
      dim_t, std::vector<StGraphPoint>(dim_s, StGraphPoint()));

  // cost_table_[i][j] = STPoint(0.0 + j * unit_s_, 0.0 + i * unit_t_);
  double curr_t = 0.0;
  for (uint32_t i = 0; i < cost_table_.size(); ++i, curr_t += unit_t_) {
    auto& cost_table_i = cost_table_[i];
    double curr_s = 0.0;
    for (uint32_t j = 0; j < cost_table_i.size(); ++j, curr_s += unit_s_) {
      cost_table_i[j].Init(i, j, STPoint(curr_s, curr_t));
    }
  }
  return Status::OK();
}

// 计算总代价
Status DpStGraph::CalculateTotalCost() {
  // col and row are for STGraph
  // t corresponding to col，横坐标
  // s corresponding to row，纵坐标
  uint32_t next_highest_row = 0;
  uint32_t next_lowest_row = 0;

  // 对于第一、二，直至最后一个时间采样值，循环计算不同距离采样值上的代价
  // 注意：每个时间采样值上的距离采样值数目是不相同的。例如：
  // 第一个时间采样值为起点，在该点上只能有一个距离采样值：0，否则
  // 代价表cost_table_就不正确。正常情况下，第二个时间采样值上的距离采样值数目
  // 会大于1，不然就是匀速前进，玩不下去了^_^
  for (size_t c = 0; c < cost_table_.size(); ++c) {
    // 最高行，即最大加速度情形下所允许的最大距离采样值
    uint32_t highest_row = 0;
    // 最低行，即最大减速度情形下所允许的最小距离采样值
    uint32_t lowest_row = cost_table_.back().size() - 1;

    // 对于时间采样值c上的不同距离采样值r: next_lowest_row<=4<=next_highest_row
    // 计算抵达节点(c, r)的最小总代价
    for (uint32_t r = next_lowest_row; r <= next_highest_row; ++r) {
      if (FLAGS_enable_multi_thread_in_dp_st_graph) {
        // 采用线程池方式计算（c, r)的最小总代价
        PlanningThreadPool::instance()->Push(
            std::bind(&DpStGraph::CalculateCostAt, this, c, r));
      } else {
        // 采用单线程方式计算(c, r)的最小总代价
        CalculateCostAt(c, r);
      }
    }
    // 线程池方式间的同步
    if (FLAGS_enable_multi_thread_in_dp_st_graph) {
      PlanningThreadPool::instance()->Synchronize();
    }

    // 给定时间采样值c的情形下，
    // 更新最高行（即最大采样距离值）和最低行（即最小采样距离值）
    for (uint32_t r = next_lowest_row; r <= next_highest_row; ++r) {
      const auto& cost_cr = cost_table_[c][r];
      if (cost_cr.total_cost() < std::numeric_limits<double>::infinity()) {
        uint32_t h_r = 0;
        uint32_t l_r = 0;
        // 获取当前节点的最高行和最低行
        GetRowRange(cost_cr, &h_r, &l_r);
        highest_row = std::max(highest_row, h_r);
        lowest_row = std::min(lowest_row, l_r);
      }
    }
    // 更新下一次循环的最高行（即最大采样距离）和
    // 最低行（即最小采样距离）
    next_highest_row = highest_row;
    next_lowest_row = std::max(next_lowest_row, lowest_row);
  }

  return Status::OK();
}

// 基于当前ST图上的点point，获取下一个允许的
// 最高行（即最大采样距离）和最低行（即最小采样距离）
void DpStGraph::GetRowRange(const StGraphPoint& point,
                            uint32_t* next_highest_row,
                            uint32_t* next_lowest_row) {
  double v0 = 0.0;
  if (!point.pre_point()) {
    // 起始点速度
    v0 = init_point_.v();
  } else {
    // 其他点速度
    v0 = (point.index_s() - point.pre_point()->index_s()) * unit_s_ / unit_t_;
  }

  // cost_table_中最后一个时间采样值所包含的距离采样值数目
  const size_t max_s_size = cost_table_.back().size() - 1;

  const double speed_coeff = unit_t_ * unit_t_;
  // 最大加速度情形下所允许的最大距离
  const double delta_s_upper_bound =
      v0 * unit_t_ + vehicle_param_.max_acceleration() * speed_coeff;
  *next_highest_row =
      point.index_s() + static_cast<uint32_t>(delta_s_upper_bound / unit_s_);
  if (*next_highest_row >= max_s_size) {
    *next_highest_row = max_s_size;
  }
  // 最大减速度情形下所允许的最小距离
  const double delta_s_lower_bound = std::fmax(
      0.0, v0 * unit_t_ + vehicle_param_.max_deceleration() * speed_coeff);
  *next_lowest_row += static_cast<int32_t>(delta_s_lower_bound / unit_s_);
  if (*next_lowest_row > max_s_size) {
    *next_lowest_row = max_s_size;
  }
}

// 使用动态规划算法计算（c, r)点的总代价
// c: 时间坐标，即横坐标
// r: 距离坐标，即纵坐标
void DpStGraph::CalculateCostAt(const uint32_t c, const uint32_t r) {
  auto& cost_cr = cost_table_[c][r];
  // 设置当前点的障碍物代价
  cost_cr.SetObstacleCost(dp_st_cost_.GetObstacleCost(cost_cr));
  // 当前点的障碍物代价无穷大，直接返回
  if (cost_cr.obstacle_cost() > std::numeric_limits<double>::max()) {
    return;
  }
  // 初始代价
  const auto& cost_init = cost_table_[0][0];
  // 第一个时间采样值为c（即时间t）== 0，因此r（即距离）必须为0，表示是起点，代价值自然设置为0.0。
  if (c == 0) {
    DCHECK_EQ(r, 0) << "Incorrect. Row should be 0 with col = 0. row: " << r;
    cost_cr.SetTotalCost(0.0);
    return;
  }

  // 获取速度限制条件
  double speed_limit =
      st_graph_data_.speed_limit().GetSpeedLimitByS(unit_s_ * r);
  // 第二个时间采样值
  if (c == 1) {
    // 加速度或减速度超出范围，返回
    const double acc = (r * unit_s_ / unit_t_ - init_point_.v()) / unit_t_;
    if (acc < dp_st_speed_config_.max_deceleration() ||
        acc > dp_st_speed_config_.max_acceleration()) {
      return;
    }

    // 当前点与初始点有重叠，返回
    if (CheckOverlapOnDpStGraph(st_graph_data_.st_boundaries(), cost_cr,
                                cost_init)) {
      return;
    }
    // 设置当前点的代价值
    cost_cr.SetTotalCost(cost_cr.obstacle_cost() + cost_init.total_cost() +
                         CalculateEdgeCostForSecondCol(r, speed_limit));
    // 设置其前序节点为起点
    cost_cr.SetPrePoint(cost_init);
    return;
  }

  constexpr double kSpeedRangeBuffer = 0.20;
  // 允许的最大距离采样差值
  const uint32_t max_s_diff =
      static_cast<uint32_t>(FLAGS_planning_upper_speed_limit *
                            (1 + kSpeedRangeBuffer) * unit_t_ / unit_s_);
  // 最小距离采样值
  const uint32_t r_low = (max_s_diff < r ? r - max_s_diff : 0);
  // 上一个时间采样值下不同采样距离的代价数组
  const auto& pre_col = cost_table_[c - 1];

  // 第三个时间采样值
  if (c == 2) {
    for (uint32_t r_pre = r_low; r_pre <= r; ++r_pre) {
      // 从距离采样值r_pre到r所需的加速度
      const double acc =
          (r * unit_s_ - 2 * r_pre * unit_s_) / (unit_t_ * unit_t_);
      // 若加速度越界，则忽略该距离采样值
      if (acc < dp_st_speed_config_.max_deceleration() ||
          acc > dp_st_speed_config_.max_acceleration()) {
        continue;
      }
      // 与前一时间采样值上的节点有重合，忽略该距离采样值
      if (CheckOverlapOnDpStGraph(st_graph_data_.st_boundaries(), cost_cr,
                                  pre_col[r_pre])) {
        continue;
      }
      // 计算当前节点（c, r)的代价值
      const double cost = cost_cr.obstacle_cost() +
                          pre_col[r_pre].total_cost() +
                          CalculateEdgeCostForThirdCol(r, r_pre, speed_limit);
      // 若新代价值比节点（c, r）的原有代价值更小，则更新当前节点（c, r)的总代价值
      if (cost < cost_cr.total_cost()) {
        cost_cr.SetTotalCost(cost);
        cost_cr.SetPrePoint(pre_col[r_pre]);
      }
    }
    return;
  }

  // 其他时间采样值
  for (uint32_t r_pre = r_low; r_pre <= r; ++r_pre) {

    // 若节点(c - 1, r_pre)上的总代价无穷大或前一次时间采样c - 1上没有前序节点，忽略该节点    
    if (std::isinf(pre_col[r_pre].total_cost()) ||
        pre_col[r_pre].pre_point() == nullptr) {
      continue;
    }
    // 从r_pre抵达r所需的加速度
    const double curr_a = (cost_cr.index_s() * unit_s_ +
                           pre_col[r_pre].pre_point()->index_s() * unit_s_ -
                           2 * pre_col[r_pre].index_s() * unit_s_) /
                          (unit_t_ * unit_t_);
    // 若加速度越界，忽略该距离采样值
    if (curr_a > vehicle_param_.max_acceleration() ||
        curr_a < vehicle_param_.max_deceleration()) {
      continue;
    }
    // 与前一时间采样值上的节点有重合，忽略该距离采样值
    if (CheckOverlapOnDpStGraph(st_graph_data_.st_boundaries(), cost_cr,
                                pre_col[r_pre])) {
      continue;
    }

    // 上上次距离采样值
    uint32_t r_prepre = pre_col[r_pre].pre_point()->index_s();
    // ST图上的上上个点
    const StGraphPoint& prepre_graph_point = cost_table_[c - 2][r_prepre];
    // 若上上个节点总代价无穷大，忽略之。
    if (std::isinf(prepre_graph_point.total_cost())) {
      continue;
    }
    // 若上上个节点没有前序节点，忽略之。
    if (!prepre_graph_point.pre_point()) {
      continue;
    }
    // 上上上个节点
    const STPoint& triple_pre_point = prepre_graph_point.pre_point()->point();
    // 上上个节点
    const STPoint& prepre_point = prepre_graph_point.point();
    // 上个节点
    const STPoint& pre_point = pre_col[r_pre].point();
    // 当前节点
    const STPoint& curr_point = cost_cr.point();
    // 计算从上上上个节点、上上个节点、上个节点与当前节点之间的最小连接代价
    double cost = cost_cr.obstacle_cost() + pre_col[r_pre].total_cost() +
                  CalculateEdgeCost(triple_pre_point, prepre_point, pre_point,
                                    curr_point, speed_limit);

    // 若新代价值比节点（c, r）的原有代价值更小，则更新当前节点（c, r)的总代价值
    if (cost < cost_cr.total_cost()) {
      cost_cr.SetTotalCost(cost);
      cost_cr.SetPrePoint(pre_col[r_pre]);
    }
  }
}

// 获取代价值最小的速度数据
Status DpStGraph::RetrieveSpeedProfile(SpeedData* const speed_data) {
  // 最小代价值
  double min_cost = std::numeric_limits<double>::infinity();
  // 最优终点(即包含最小代价值的节点)
  const StGraphPoint* best_end_point = nullptr;
  //  cost_table_.back()存储的是最后一个时间采样值上不同距离的代价值
  for (const StGraphPoint& cur_point : cost_table_.back()) {
    if (!std::isinf(cur_point.total_cost()) &&
        cur_point.total_cost() < min_cost) {
      best_end_point = &cur_point;
      min_cost = cur_point.total_cost();
    }
  }
  // 对于cost_table_中的每一行，即第一个、第二个、...、最后一个时间采样值上的
  // 代价值数组，其最后一个元素存储的是本级时间采样值上的最小代价节点。
  // 将这些节点与现有最优终点best_end_point比较，
  // 不断更新最小代价值min_cost和最优终点best_end_point，
  // 直至找到全局最优终点
  for (const auto& row : cost_table_) {
    const StGraphPoint& cur_point = row.back();
    if (!std::isinf(cur_point.total_cost()) &&
        cur_point.total_cost() < min_cost) {
      best_end_point = &cur_point;
      min_cost = cur_point.total_cost();
    }
  }

  // 寻找最优终点失败
  if (best_end_point == nullptr) {
    const std::string msg = "Fail to find the best feasible trajectory.";
    AERROR << msg;
    return Status(ErrorCode::PLANNING_ERROR, msg);
  }

  // 设置最优终点的速度数据，并顺藤摸瓜找出其连接的倒数第二个、倒数第三个直到第一个时间节点
  // 分别设置这些时间节点的速度数据
  std::vector<SpeedPoint> speed_profile;
  const StGraphPoint* cur_point = best_end_point;
  while (cur_point != nullptr) {
    SpeedPoint speed_point;
    speed_point.set_s(cur_point->point().s());
    speed_point.set_t(cur_point->point().t());
    speed_profile.emplace_back(speed_point);
    cur_point = cur_point->pre_point();
  }
  // 将速度数据按起点到终点的顺序重新排列
  std::reverse(speed_profile.begin(), speed_profile.end());

  // 若速度数据中起始点的时间（t）或距离（s）大于编译器定义的最小双精度浮点数（即起点的时间t
  // 或距离s不为0），则视结果为错误输出。
  constexpr double kEpsilon = std::numeric_limits<double>::epsilon();
  if (speed_profile.front().t() > kEpsilon ||
      speed_profile.front().s() > kEpsilon) {
    const std::string msg = "Fail to retrieve speed profile.";
    AERROR << msg;
    return Status(ErrorCode::PLANNING_ERROR, msg);
  }

  // 设置最终的速度数据
  speed_data->set_speed_vector(speed_profile);
  return Status::OK();
}

// 计算第一、二、三、四个节点之间的连接代价
double DpStGraph::CalculateEdgeCost(const STPoint& first, const STPoint& second,
                                    const STPoint& third, const STPoint& forth,
                                    const double speed_limit) {
  return dp_st_cost_.GetSpeedCost(third, forth, speed_limit) +
         dp_st_cost_.GetAccelCostByThreePoints(second, third, forth) +
         dp_st_cost_.GetJerkCostByFourPoints(first, second, third, forth);
}

// 为第二列（即第三个时间采样值上的代价数组）计算连接代价
double DpStGraph::CalculateEdgeCostForSecondCol(const uint32_t row,
                                                const double speed_limit) {
  double init_speed = init_point_.v();
  double init_acc = init_point_.a();
  const STPoint& pre_point = cost_table_[0][0].point();
  const STPoint& curr_point = cost_table_[1][row].point();
  return dp_st_cost_.GetSpeedCost(pre_point, curr_point, speed_limit) +
         dp_st_cost_.GetAccelCostByTwoPoints(init_speed, pre_point,
                                             curr_point) +
         dp_st_cost_.GetJerkCostByTwoPoints(init_speed, init_acc, pre_point,
                                            curr_point);
}

// 为第三列（即第四个时间采样值上的代价数组）计算连接代价
double DpStGraph::CalculateEdgeCostForThirdCol(const uint32_t curr_row,
                                               const uint32_t pre_row,
                                               const double speed_limit) {
  double init_speed = init_point_.v();
  const STPoint& first = cost_table_[0][0].point();
  const STPoint& second = cost_table_[1][pre_row].point();
  const STPoint& third = cost_table_[2][curr_row].point();
  return dp_st_cost_.GetSpeedCost(second, third, speed_limit) +
         dp_st_cost_.GetAccelCostByThreePoints(first, second, third) +
         dp_st_cost_.GetJerkCostByThreePoints(init_speed, first, second, third);
}