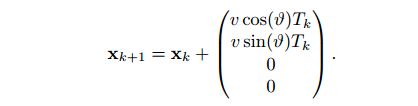3月16日 CV,CA,CTRV等运动模型,EKF,UKF在运动模型下的分析与实践
文章目录
- 一次运动模型(也别称为线性运动模型)
- 1.0 匀速模型(Constant Velocity, CV)
- 版本一
- 版本二:
- 1.1 状态转移方程
- 1.2 局限
- 2.0 匀加速模型(Constant Acceleration, CA)
- 2.1 状态转移方程
- 二次运动模型:
- 1.0 恒定转弯率和速度幅度模型(Constant Turn Rate and Velocity, CTRV)
- 模型的一个问题:角速度ω=0( ω = ψ ^ ω=\hat{\psi} ω=ψ^是角速度)
- 1.1 该模型运用EKF的例子
- UKE实例
- 1.0 非线性处理/测量模型
- 2.0 无损变换
- 预测
- 由一个高斯分布产生sigma point
- 预测sigma point
- 预测均值和方差
- 测量更新
- 更新状态
- 伪代码分析:
- UKF=UT+KF
- 简化UKF滤波算法(加性噪声)
- 扩维UKF滤波算法(噪声隐含)
- 参数估计/学习(之后可以拓展学习)
- 参考资料:
- 恒定转动率和加速度(CTRA)
- 恒定转向角和速度(CSAV)
- 恒定曲率和加速度(CCA)(Constant Curvature and Acceleration, CCA)
修订
- 20200324 CTRV模型
一次运动模型(也别称为线性运动模型)
- 链接:https://blog.csdn.net/AdamShan/article/details/78265754
恒定速度模型(Constant Velocity, CV)
恒定加速度模型(Constant Acceleration, CA)
这些线性运动模型假定目标是直线运动的,并不考虑物体的转弯。
1.0 匀速模型(Constant Velocity, CV)
在扩展卡尔曼滤波课程中,我们使用了一个等速模型(CV)。等速模型是用于物体跟踪的最基本的运动模型之一。
版本一
转移函数为:
版本二:
![]()
四个状态变量依次为横坐标,纵坐标,与x轴夹角(逆时针为正),线速度
1.1 状态转移方程
1.2 局限
等速(CV)模型(速度是常量的模型)的局限性:
假设速度是常量,我们实际上简化了车辆实际移动的形式,因为大多数车辆道路是有拐弯的,但速度是常量的模型会无法正确预测拐弯车辆。
2.0 匀加速模型(Constant Acceleration, CA)
![]()
四个状态变量依次为横坐标,纵坐标,与x轴夹角(逆时针为正),线速度,加速度
2.1 状态转移方程
二次运动模型:
-
恒定转率和速度模型(Constant Turn Rate and Velocity,CTRV)
-
恒定转率和加速度模型(Constant Turn Rate and Acceleration,CTRA)
CTRV目前多用于机载追踪系统(飞机),这些二次运动模型大多假定速度 v和 偏航角速度(yaw rate)ω 没有关系,因此,在这类运动模型中,由于**偏航角速度ω **测量的扰动(不稳定),即使车辆没有移动,我们的运动模型下的角速度也会发生细微的变化。 -
为了解决这个问题,速度 v 和 偏航角速度 ω 的关联可以通过设定转向角 Φ 恒定来建立,这样就引出了 恒定转向角和速度模型(Constant Steering Angle and Velocity,CSAV), 另外,速度可以别假定为线性变化的,进而引出了常曲率和加速度模型(Constant Curvature and Acceleration,CCA)。
-
论文参考:Empirical evaluation of vehicular models for ego motion estimation

图片:论文:Empirical evaluation of vehicular models for ego motion estimation
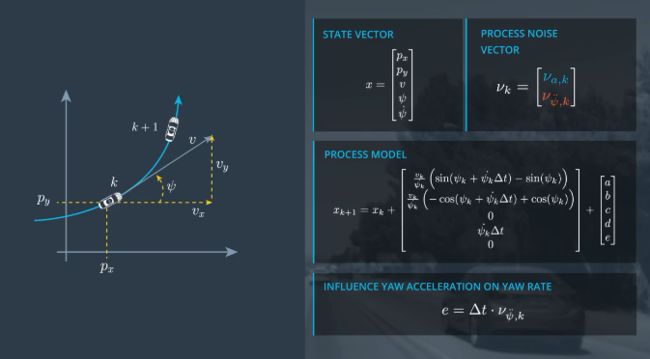
1.0 恒定转弯率和速度幅度模型(Constant Turn Rate and Velocity, CTRV)
CTRV实际上是CV的一般形式,当角速度=0时(这里需要用到洛必达法则),就是CV的形式。CTRV模型假设对象沿直线前进,同时还能以固定的转弯速率和恒定的速度大小移动。可以看做一段圆弧运动
四个状态变量依次为横坐标,纵坐标,速度大小用v表示;第四个参数是偏航角,表示方向;第五个参数是估算的角速度。


一个恒定的转弯率,就像在ctrv模型中那样,角速度的变化率是0

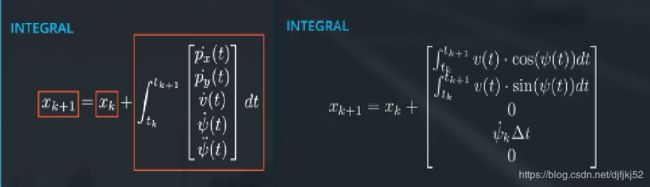
假设离散的时间步骤 k k k和持续的时间值 t k t_k tk相关,离散的时间步骤 k + 1 k+1 k+1和持续的时间值 t k + 1 t_{k+1} tk+1相关, t k + 1 t_{k+1} tk+1可 t k t_k tk之间的时间差叫做 δ t \delta t δt.
模型的一个问题:角速度ω=0( ω = ψ ^ ω=\hat{\psi} ω=ψ^是角速度)
使用CTRV还存在一个问题,那就是 ω=0 的情况,此时我们的状态转移函数公式中的 (x,y) 将变成无穷大。为了解决这个问题,我们考察一下 ω=0 的情况,此时我们追踪的车辆实际上是直线行驶的,所以我们的 (x,y) 的计算公式就变成了:
x ( t + Δ t ) = v c o s ( ψ ) Δ t + x ( t ) x(t+Δt)=vcos(\psi )Δt+x(t) x(t+Δt)=vcos(ψ)Δt+x(t)
y ( t + Δ t ) = v s i n ( ψ ) Δ t + y ( t ) y(t+Δt)=vsin(\psi )Δt+y(t) y(t+Δt)=vsin(ψ)Δt+y(t)
注意: ψ \psi ψ是值得角度, ψ ^ \hat{\psi} ψ^是角速度, ψ ^ ^ \hat{\hat{\psi}} ψ^^角加速度
角速度为0时:

1.1 该模型运用EKF的例子
- 链接:https://blog.csdn.net/AdamShan/article/details/78265754

其中,θ 为偏航角,是追踪的目标车辆在当前车辆坐标系下与x轴的夹角,逆时针方向为正,取值范围是[0, 2π), ω是偏航角速度。

由于EKF采用:


在我们后面的Python实现中,我们将使用numdifftools包直接计算雅可比矩阵,而不需要我们使用代码写这个雅可比矩阵。在得到我们CTRV模型的雅可比矩阵以后,我们的处理模型就可以写成:

处理噪声
处理噪声模拟了运动模型中的扰动,我们引入运动模型的出发点就是要简化我们要处理的问题,这个简化是建立在多个假设的基础上(在CTRV中,这些假设就是恒定偏航角速度和速度),但是在现实问题中这些假设就会带来一定的误差,处理噪声实际上描述了当我们的系统在运行一个指定时间段以后可能面临多大的这样的误差。
在CTRV模型中噪声的引入主要来源于两处:直线加速度和偏航角加速度噪声,我们假定直线加速度和偏航角加速度满足均值为 0,方差分别为 σ a 2 , σ ω ˙ 2 σ^2_a, σ^2_{ω˙} σa2,σω˙2的高斯分布,由于均值为 0, 我们在状态转移公式中的 u就可以不予考虑,我们来看噪声带来的不确定性 Q ,直线加速度和偏航角加速度将影响我们的状态量 ( x , y , v , θ , ω ) (x,y,v,θ,ω) (x,y,v,θ,ω) ,这两个加速度量对我们的状态的影响的表达式如下:

其中 μ a , μ ω ˙ μ_a,μ_{ω˙} μa,μω˙ 为直线上和转角上的加速度(在这个模型中,我们把把它们看作处理噪声),我们分解这个矩阵:
测量
激光雷达:测量目标车辆的坐标 (x,y) 。这里的x,y是相对于我们的车辆的坐标系的,即我们的车辆为坐标系的原点,我们的车头为x轴,车的左侧为y轴。
雷达:测量目标车辆在我们车辆坐标系下与本车的距离 ρ,目标车辆与x轴的夹角 ψ,以及目标车辆与我们自己的相对距离变化率 ρ˙(本质上就是目标车辆的实际速度在我们和目标车辆的连线上的分量)
雷达的预测映射到测量空间是非线性的,其表达式为:

虽然这个雅可比矩阵看似非常复杂,但是我们待会编程的时候并不需要完整的推导出这个雅可比矩阵的表达式,在本篇中,我们采用numdifftools这个公式来直接求解雅可比矩阵。
代码:
请移步至:https://blog.csdn.net/AdamShan/article/details/78265754
UKE实例
- https://blog.csdn.net/AdamShan/article/details/78359048
1.0 非线性处理/测量模型
我们知道我们在应用KF是面临的主要问题就是非线性处理模型(比如说CTRV)和非线性测量模型(RADAR测量)的处理。我们从概率分布的角度来描述这个问题:
对于我们想要估计的状态,在k时刻满足均值为 x k ∣ k x_{k|k} xk∣k ,方差为 P k ∣ k P_{k|k} Pk∣k 这样的一个高斯分布,这个是我们在k时刻的 后验(Posterior)(如果我们把整个卡尔曼滤波的过程迭代的来考虑的话),现在我们以这个后验为出发点,结合一定的先验知识(比如说CTRV运动模型)去估计我们在 k+1 时刻的状态的均值和方差,这个过程就是卡尔曼滤波的预测,如果变换是线性的,那么预测的结果仍然是高斯分布,但是现实是我们的处理和测量模型都是非线性的,结果就是一个不规则分布,KF能够使用的前提就是所处理的状态是满足高斯分布的,为了解决这个问题,EKF是寻找一个线性函数来近似这个非线性函数,而UKF就是去找一个与真实分布近似的高斯分布。

UKF的基本思路就是: 近似非线性函数的概率分布要比近似非线性函数本身要容易!
那么如何去找一个与真实分布近似的高斯分布呢?——找一个与真实分布有着相同的均值和协方差的高斯分布。
那么如何去找这样的均值和方差呢?——无损变换。
2.0 无损变换
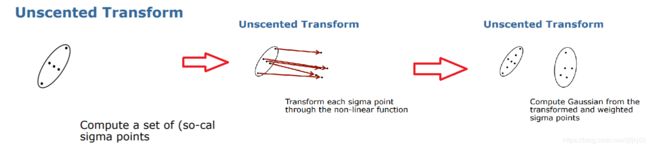
计算一堆点(术语叫做sigma point),通过一定的手段产生的这些sigma点能够代表当前的分布,然后将这些点通过非线性函数(处理模型)变换成一些新的点,然后基于这些新的sigma点计算出一个高斯分布(带有权重地计算出来)如图:
有点粒子滤波的意思,可以移步至https://blog.csdn.net/djfjkj52/article/details/104562430,了解例子滤波的理解。
- 计算一组sigma点
- 每个sigma点都有权重
- 通过非线性函数变换点
- 根据加权点计算高斯
预测
χ χ χ——Chi,是第二十二个希腊字母。 χ的ch是一个清软颚擦音
λ λ λ——Lambda,是第十一个希腊字母。 大写Λ用于: 粒子物理学上,Λ重子的符号
由一个高斯分布产生sigma point
通常,假定状态的个数为 n ,我们会产生 2n+1 个sigma点,其中第一个就是我们当前状态的均值 μ ,sigma点集的均值的计算公式为:
其中的 λ 是一个超参数,根据公式,λ 越大, sigma点就越远离状态的均值,λ 越小, sigma点就越靠近状态的均值。
需要注意的是,在我们的CTRV模型中,状态数量 n 除了要包含5个状态以外,还要包含处理噪声 μa 和 μω˙,因为这些处理噪声对模型也有着非线性的影响。在增加了处理噪声的影响以后,我们的不确定性矩阵 P 就变成了:
其中,P′ 就是我们原来的不确定性矩阵(在CTRV模型中就是一个 5×5 的矩阵),Q是处理噪声的协方差矩阵,在CTRV模型中考虑到直线加速度核Q的形式为:
以上公式中还存在一个问题,那就是矩阵开平方根怎么计算的问题?
需要求解:

其中,可得:


求解上式中的 A 是一个相对复杂的过程,但是如果 P 是对角矩阵的话,那么这个求解就会简化,在我们的实例中,P表示对估计状态的不确定性(协方差矩阵),我们会发现 P 基本上是对角矩阵(状态量之间的相关性几乎为0), 所以我们可以首先对 P 做 Cholesky分解(Cholesky decomposition) ,然后分解得到的矩阵的下三角矩阵就是我们要求的 A ,在这里我们就不详细讨论了,在我们后面的实际例子中,我们直接调用库中相应的方法即可
c++
MatrixXd A = P_aug.llt().matrixL();
预测sigma point
现在我们有sigma点集,我们就用非线性函数 g() 来进行预测:

需要注意的是,这里的输入 χ k χ_k χk 是一个 (7x15) 的矩阵(因为考虑了两个噪声量),但是输出 χ k + 1 ∣ k χ_{k+1|k} χk+1∣k 是一个(5x15) 的矩阵(因为这是预测的结果,本质上是基于运动模型的先验,先验中的均值不应当包含 a , ω˙ 这类不确定的量)
预测均值和方差
首先要计算出各个sigma点的权重,权重的计算公式为:
然后基于每个sigma点的权重去求新的分布的均值和方差:
其中 μ′ 即为我们基于CTRV模型预测的目标状态的先验分布的均值 x k + 1 ∣ k x_{k+1|k} xk+1∣k ,它是sigma点集中每个点各个状态量的加权和, P′ 即为先验分布的协方差(不确定性) P_{k+1|k} , 由每个sigma点的方差的加权和求得。至此,预测的部分也就走完了,下面进入了UKF的测量更新部分。

测量更新
预测测量(将先验映射到测量空间然后算出均值和方差)
假设:测量更新分为两个部分,LIDAR测量和RADAR测量,其中LIDAR测量模型本身就是线性的,所以我们重点还是放在RADAR测量模型的处理上面,RADAR的测量映射函数为:

这也是个非线性函数,我们用 h() 来表示它,再一次,我们使用无损转换来解决,但是这里,我们可以不用再产生sigma points了,我们可以直接使用预测出来的sigma点集,并且可以忽略掉处理噪声部分。那么对先验的非线性映射就可以表示为如下的sigma point预测(即预测非线性变换以后的均值和协方差):
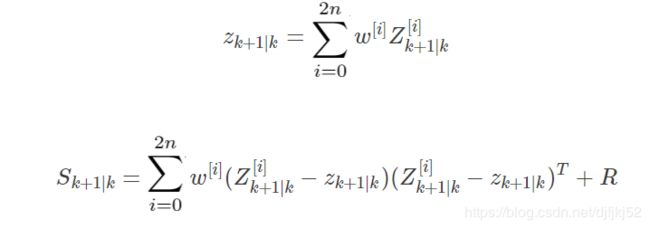
和前面的文章一样,这里的 R 也是测量噪声,在这里我们直接将测量噪声的协方差加到测量协方差上是因为该噪声对系统没有非线性影响。在本例中,以RADAR的测量为例,那么测量噪声R为:

更新状态
首先计算出sigma点集在状态空间和测量空间的互相关函数,计算公式如下

更新状态(也就是作出最后的状态估计):

其中 z k + 1 z_{k+1} zk+1是新得到的测量,而 z k + 1 ∣ k z_{k+1|k} zk+1∣k 则是我们根据先验计算出来的在测量空间的测量。
伪代码分析:
预测:
更新
UKF=UT+KF
- https://blog.csdn.net/weixin_42647783/article/details/89065436?depth_1-utm_source=distribute.pc_relevant.none-task&utm_source=distribute.pc_relevant.none-task
UKF=UT+KF,算法的实现分成两步走:
(1)状态的时间更新
选定状态的个Sigma点;
利用UT变换计算后验均值和方差;
(2)状态的观测更新
利用标准的卡尔曼滤波体系更新,但使用的公式有所差异。
根据系统的噪声的存在方式,将其分为加性噪声和隐含噪声,对于两种噪声,UKF滤波的处理方式分为两种,分别是简化的UKF和扩维的UKF,这里仍然假设噪声是高斯分布的。
简化UKF滤波算法(加性噪声)
可以参考:https://blog.csdn.net/weixin_42647783/article/details/89065436?depth_1-utm_source=distribute.pc_relevant.none-task&utm_source=distribute.pc_relevant.none-task
扩维UKF滤波算法(噪声隐含)
参数估计/学习(之后可以拓展学习)
没有做参数估计的UKF滤波,Adaptive-UKF在估计误差上与UKF滤波相差不大,但它并不需要指定状态转移噪声和观测噪声的参数,将更有利于在实际中的应用。
利用EM算法和极大后验概率估计(MAP),对未知的噪声参数做出估计,再利用估计出的参数去递推卡尔曼滤波的解。每做完一轮UKF滤波,就可以更新一次参数,用于下一轮的UKF滤波。
参考资料:
pdf:
-
http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.136.6539&rep=rep1&type=pdf
-
https://www.cse.sc.edu/~terejanu/files/tutorialUKF.pdf
PPT:
- http://ais.informatik.uni-freiburg.de/teaching/ws13/mapping/pdf/slam06-ukf-4.pdf
恒定转动率和加速度(CTRA)
(Constant Turn Rate and Acceleration, CTRA)
同CTRV相比,转速不变,说明在相同时间内转过的角度是一样的,径向由匀速变成匀加速,那么对应的,位移会变长。
![]()


恒定转向角和速度(CSAV)
该CSAV模型网络上的资料不多,后续需要补充
恒定曲率和加速度(CCA)(Constant Curvature and Acceleration, CCA)
CTRA中的转速一定改为曲率半径一定,由 r = v / ω r=v/ω r=v/ω可知,当曲率半径一定,又要做匀加速运动,那么角速度必然是时变的,因此同样时间内转过的角度必然会增大。CTRV(黑),CTRA(橘),CCA(红)的关系如下图所示
该CCA模型网络上的资料不多,后续需要补充