apollo学习笔记三：预测、规划与控制

1.预测

预测模块具有实时性、准确性、自主学习的特点。有两种基本的预测框架，一种是基于模型的，一种是数据驱动的。

基于模型的预测基于规则与概率，通过穷尽当前状况的可能发生的合理的结果，并通过预测对象下一步的行动来增强某一结果可能发生的概率。
数据驱动的预测基于行为与数据，一般来说，数据越多，预测模型效果越好。

车道序列框架

apollo使用车道序列框架，为道路上的物体生成轨迹。为了生成车道序列框架，我们将道路分为多个部分，每一部分将覆盖一个易于描述车辆运动的区域。为了预测，我们更关心车辆如何在这些区域内转换，而不是在某个区域内的具体行为，我们可以将车辆的行为划分为一组有限的模式组合，并将这些模式组合描述为车道序列。

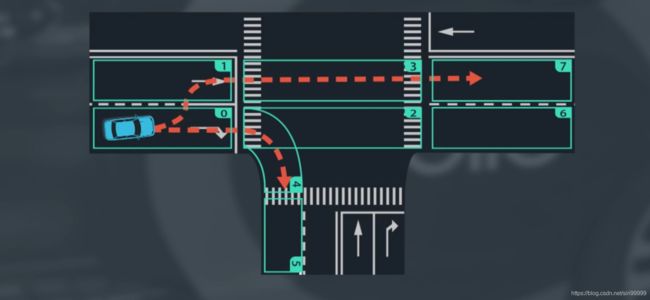
如图所示，蓝色汽车在十字路口将有两个显而易见的选择：一是右转，其车道序列为0-4-5；二是直行，其车道序列为0-1-3-7.
使用车道序列进行分析，可以将预测问题简化为选择问题。接下来便是通过计算每个车道序列的概率进行选择。
此时我们需要模型，将车辆状态和车道段作为输入，模型输出选择每个车道序列的概率。

apollo使用RNN（循环神经网络）建立上述模型来预测车辆的目标车道。基础的神经网络只在层与层之间建立了权连接，RNN最大的不同之处就是在层之间的神经元之间也建立的权连接，以实现“记忆功能”。

预测的最后一步是轨迹生成，我们注意车辆在两点的位置和方位，表示运动模型的初始状态和最终状态，我们可以使用这两个条件与车辆物理来拟合一个多项式模型进行预测。

2.规划

在规划中，我们通过结合高精度地图，定位和预测来构建车辆轨迹。规划第一步为路线导航，侧重于如何从地图上的A前往B，在进行路线规划时，将地图数据作为输入，并输出可行驶路线。在构建高水平路线后，我们会放大至轨迹规划，通过轨迹规划我们可以做出微妙的调整，以避开障碍物并为乘客创造平稳的乘车体验，轨迹规划的目标是生成免碰撞和舒适的可执行轨迹。轨迹由一系列点定义，每个点都有一个关联速度和一个何时应抵达那个点的时间戳。
路径规划可分为两大部分，一部分我将其称为“宏观”，如同当下导航所实现的，输入目的地以可规划出行使路线；另一部分我将其称为“微观”，其为无人驾驶车具体驾驶过程中的移动，如变道，转弯，掉头等动作。

“宏观”规划

路径规划中，将地图转化为数据结构中的“图”进行分析，相关算法有A算法等。
A算法： f(n) = g(n) + h(n) ， 其中f(n) 是节点n的估价函数，g(n)实在状态空间中从初始节点到n节点的实际代价，h(n)是从n到目标节点最佳路径的估计代价。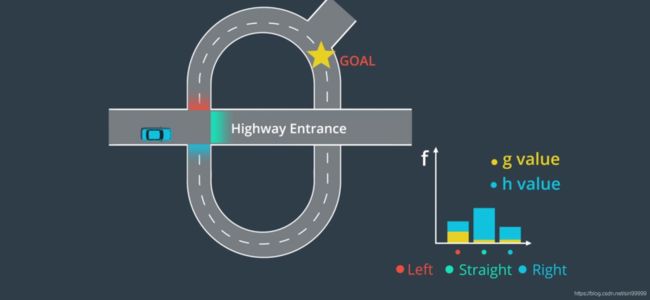

“微观”规划

轨迹生成的目标是生成一系列路径点所定义的轨迹，我们为每个路径点分配一个时间戳和速度，我们让一条曲线与这些路径点拟合，生成轨迹的几何表征。由于移动的障碍物可能会暂时阻挡部分路段轨迹中的每个路点都有时间戳，我们可以将时间戳与预测模块的输出相结合，以确保在我们的计划通过时轨迹上的每个路径点均未被占用。

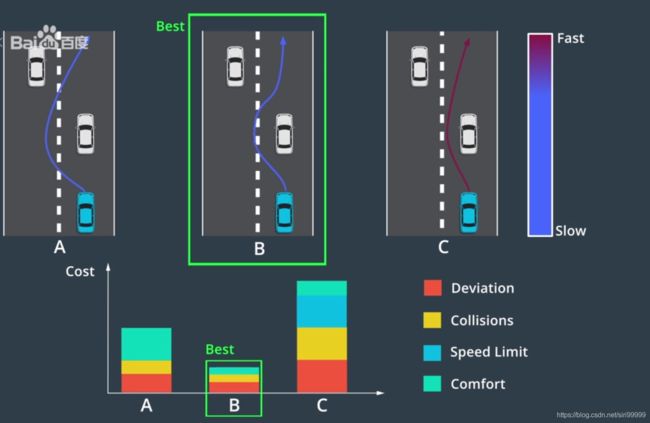
轨迹生成之后，我们使用成本函数评估每一条轨迹，成本函数为每个轨迹分配一个“成本”，“成本”包括路径上是否有障碍，变化是否平滑，是否违背汽车物理规律，是否符合交通法规等。最后选择成本函数最低的轨迹。

Frenet坐标系

Frenet坐标系又称Frenet–Serret公式，Frenet–Serret公式用于描述粒子在三维欧氏空间内沿一条连续可微曲线的运动学特征。

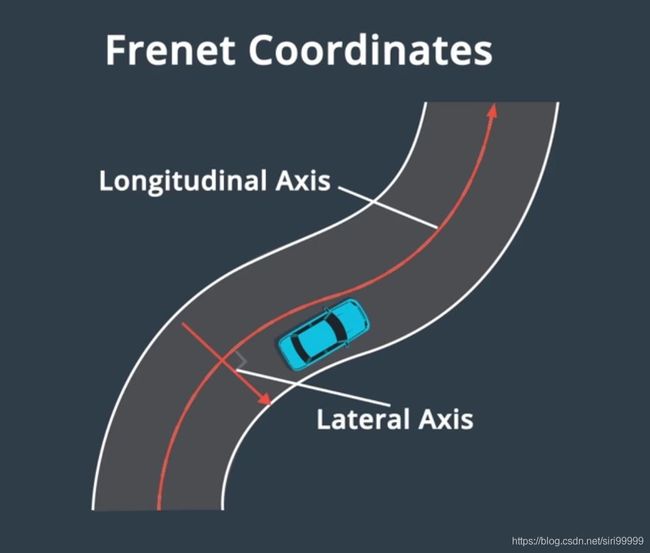
纵轴沿曲线运动方向的向量；横轴在当前曲线运动平面内时时刻刻垂直于纵坐标的向量。

路径-速度解耦规划

综述：路径-速度解耦规划将路径规划分为路径规划和速度规划两部分。 在路径规划步骤中生成候选曲线，使用成本函数对每条路径进行评估，该函数包含平滑度，安全性与车道中心的偏离，以及其他要考虑的因素，选择成本最低的路径。速度规划中确定沿这条路线行进的速度，即与路径点相关的一系列速度，而不是单个速度，我们将该序列称作“速度曲线”，使用优化功能为路径选择受到各种限制的良好速度曲线，通过将路径和速度曲线相结合，构建车辆行驶轨迹。

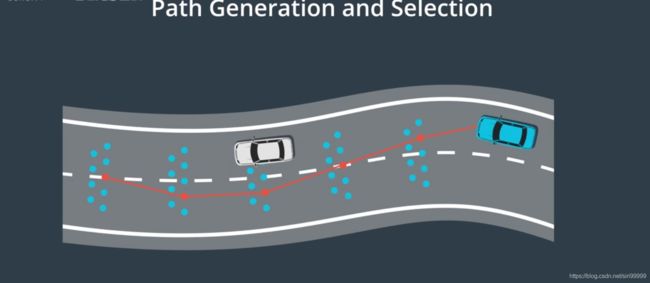
1.路径选择设计将道路划分为单元格，如图所示，蓝色点代表生成的一系列路径点，红色为选择出的最优路径。

2.速度规划涉及将S-T图（即高中物理的路程-时间图）划分为单元格，如图所示，黄色区域为某时段阻碍道路的障碍物，浅白色曲线为规划出的路线，白色曲线为选择出的最优规划路线，由高中物理可得，曲线斜率为速度。

Lattice规划

将纵向维度，横向维度，时间维度构成的三维问题分解为两个二维问题，其中一个二维轨迹为S-T图像，另一个二位轨迹为Frenet坐标系下的L-S图像。S为沿曲线运动方向的向量，L为垂直于运动方向的偏移量，T为时间。

控制

对于汽车而言，最基本的控制输入为转向，加速和制动。控制器需要拥有准确，可行，平稳等特点，即使用可行的控制输入，最大限度的降低与目标轨迹的偏差，最大限度地提高乘客的舒适度。
控制器预计有两种输入，目标轨迹与车辆状态。目标轨迹来自规划模块，在每个规划点规划模块指定一个位置和一个参考速度，在每个时间部对规划点进行更新；车辆状态包括车辆位置，速度，转向和加速度等，来自汽车内部模块。
控制器的输出是控制输入（转向、加速和制动）的值。

PID（比例，积分，微分控制）

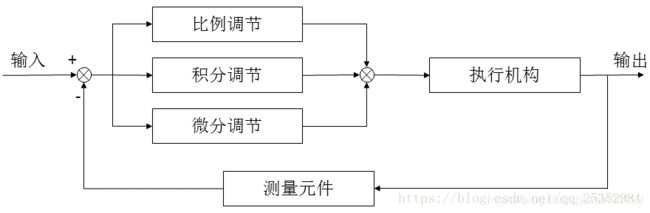
1.比例调节（P控制器）：在车辆出现偏差时，将其拉回目标轨迹。偏差越大，将其拉回目标轨迹越困难。
2.积分调节（I控制器）：消除稳态误差。
3.微分调节（D调节器）：最大限度地减少控制器输出的变化速度。

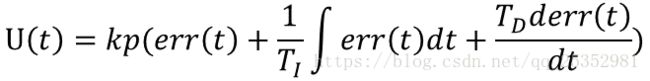
括号内，第一项为比例，第二项为积分，第三项为微分。

LQR（线性二次调节器）

使用LQR进行横向控制，横向控制包括四个组件;横向误差，横向误差变化率，朝向误差，朝向误差变化率这四个组件组成x集合，x捕获车辆状态；三个控制输入，转向，加速和制动，组成u集合。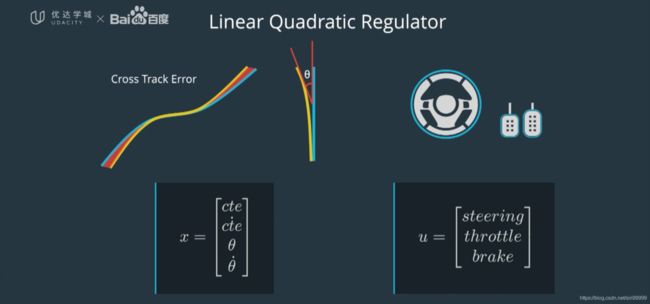
LQR模型用等式表示如图所示：
为了让误差最小化，但我们也希望尽可能少地使用控制输入。由于使用这些会有成本，例如：耗费气体或电力。为了尽量减少这些因素，我们可以保持误差的运行总和和控制输入的运行总和。当车往右转的特别厉害之际，添加到误差总和中。当控制输入将汽车往左侧转时，从控制输入总和中减去一点。然而，这种方法会导致问题。因为右侧的正误差只需将左侧的负误差消除即可。对控制输入来说也是如此。相反，我们可以让x和u与自身相乘，这样负值也会产生正平方，我们称这些为二次项。我们为这些项分配权重，并将它们加在一起。
最优的u应该最小化二次项的和随时间的积分。在数学中我们将这个积分值称为成本函数（形式见下图）。我们经常以紧凑的矩阵形式表示加权二次项的总和。

MPC（模型预测控制）

模型预测控制（或MPC）是一种更复杂的控制器，它非常依赖于数学优化，但基本上可以将MPC归结为三个步骤：1、建立车辆模型。2、使用优化引擎计算有限时间范围内的控制输入。3、执行第一组控制输入。MPC是一个重复过程，它着眼未来，计算一系列控制输入，并优化该序列。但控制器实际上只实现了序列中的第一组控制输入，然后控制器再次重复该循环。为什么我们不执行整个控制输入序列呢？那是因为我们只采用了近似测量与计算。如果实现了整个控制输入序列，实际产生的车辆状态与我们的模型有很大差异，最好在每个时间步不断地重新评估控制输入的最优序列。

MPC的第一步为定义车辆模型，该模型近似于汽车的物理特性，该模型估计了假如将一组控制输入应用于车辆时会发生什么。接下来，我们决定MPC预测未来的能力。预测越深入，控制器就越精确，不过需要的时间也越长。所以，我们需要在准确度与快速获取结果之间做出取舍。获取结果的速度越快，越能快速地将控制输入应用到实际车辆中。

下一步是将模型发送到搜索最佳控制输入的优化引擎。该优化引擎的工作原理是通过搜索密集数学空间来寻求最佳解决方案。为缩小搜索范围，优化引擎依赖于车辆模型的约束条件。

优化引擎可间接评估控制输入，它通过使用以下方法对车辆轨迹进行建模：通过成本函数对轨迹进行评估。成本函数主要基于与目标轨迹的偏差；其次，基于其他因素，如加速度和提升旅客舒适度的措施。

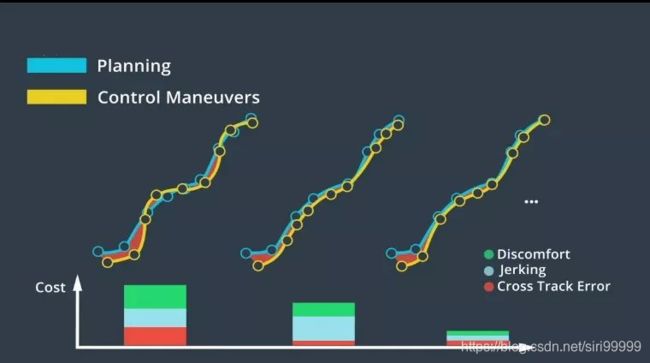
为使乘客感觉更舒适，对控制输入的调整应该很小。因为动作变化幅度过大会让乘客感到不舒服。根据具体情况，我们可能需要为其考虑进一步的成本，并设计成本函数。模型、约束和成本函数合并在一起，并作为优化问题加以解决。我们可以在不同的优化引擎中，选择一种来寻找最佳解决方案。