【佛山市选2013】JZOJ2020年8月7日提高组T2 树环转换
【佛山市选2013】JZOJ2020年8月7日提高组T2 树环转换
题目
描述
给定一棵N个节点的树,去掉这棵树的一条边需要消耗值1,为这个图的两个点加上一条边也需要消耗值1。树的节点编号从1开始。在这个问题中,你需要使用最小的消耗值(加边和删边操作)将这棵树转化为环,不允许有重边。
环的定义如下:
- 该图有N个点,N条边。
- 每个顶点的度数为2。
- 任意两点是可达的。
树的定义如下:
- 该图有N个点,N-1条边。
- 任意两点是可达的。
数据
对于20%的数据,有1≤N≤10。
对于100%的数据,有1≤N≤1000000。
题解
题意
给出一棵树
每次删边加边的代价都为一
问最小代价将树转成环
分析
看到树呢,很容易 (个屁) 想到树形DP
但是如果直接设状态的话不好转移
思考:环是什么
不就是一条链再加上一条边吗
一条链是什么
特殊的树呀!
那么就可以设 f [ i ] f[i] f[i]表示以 i i i为根的子树转成链的最小代价
如果想去推方程的话,先别急
我们来看一下什么是链

一张丑陋的图
很容易发现
除了第一个和最后一个点
其他节点的度数都为2
那么是不是可以设 f [ i ] [ 0 ] f[i][0] f[i][0]表示根节点 i i i转换成链之后是两个端点中的一个的最小代价, f [ i ] [ 1 ] f[i][1] f[i][1]表示不管 i i i的位置的最小代价
放方程:
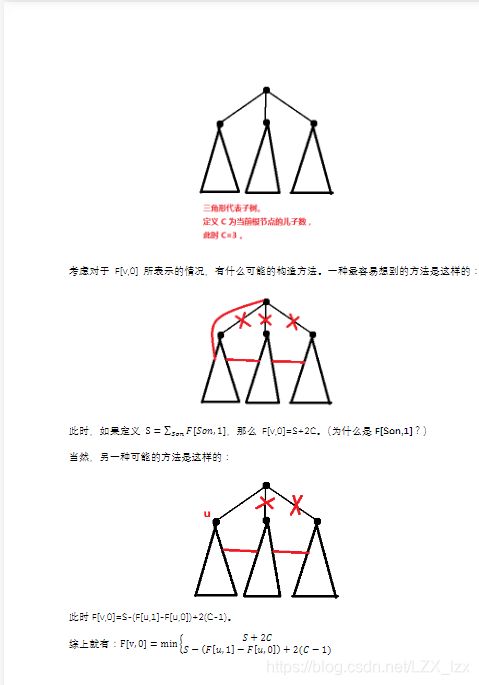
告知: S S S表示 ∑ f [ s o n ] [ 1 ] \sum_\ f[son][1] ∑ f[son][1], c c c表示儿子的个数, u , v u,v u,v是 i i i的儿子
f [ i ] [ 0 ] = m i n { S + 2 c S − ( f [ u ] [ 1 ] − f [ u ] [ 0 ] ) + 2 ∗ ( c − 1 ) f[i][0]=min\begin{cases}S+2c\\S-(f[u][1]-f[u][0])+2*(c-1)\end{cases} f[i][0]=min{S+2cS−(f[u][1]−f[u][0])+2∗(c−1)
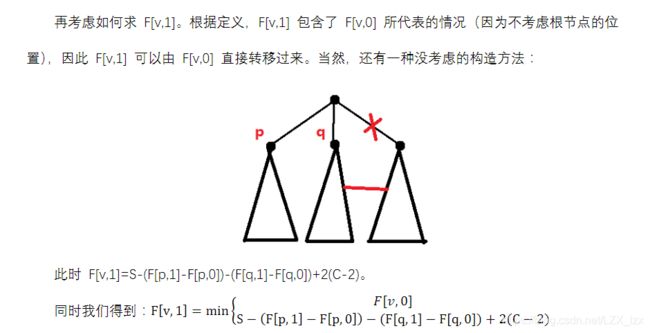
f [ i ] [ 1 ] = m i n { f [ i ] [ 0 ] S − ( f [ u ] [ 1 ] − f [ u ] [ 0 ] + 2 ∗ ( c − 2 ) f[i][1]=min\begin{cases}f[i][0]\\S-(f[u][1]-f[u][0]+2*(c-2)\end{cases} f[i][1]=min{f[i][0]S−(f[u][1]−f[u][0]+2∗(c−2)
小小的优化:
对于 u , v u,v u,v的话,既然要使更小,那么 f [ u ] [ 1 ] − f [ u ] [ 0 ] f[u][1]-f[u][0] f[u][1]−f[u][0]之类的就要最大
记一下最大和次大就可以了
至于解释的话
另外就是
本题卡系统栈!!!
所以你可以打 B F S BFS BFS或者开人工栈
Code
#include