【JZOJ5057】【GDSOI2017模拟4.13】炮塔
Description
A君正在玩一款战略游戏,游戏中的规则是这样的:
给定一个n*m的地图,地图上每一个位置要么是空地,要么是炮塔,要么有若干数量的敌人。现在A君要操控炮塔攻击这些敌人。
对于每个炮塔,它们的攻击方向已经确定(上下左右其中一个),A君只需要为每个炮塔指定攻击位置。每一个炮塔只能朝它攻击方向上的某个位置进行攻击,每个炮塔只能攻击一次,当然,炮塔也可以不进行攻击。炮塔对一个位置攻击后,位置上的所有敌人都会被消灭。
现在,游戏已经保证不存在一个炮塔能够攻击另一个炮塔的情况。但是,若把炮塔的位置与其攻击位置间的连线称为炮弹的运行轨迹,那么A君的攻击方案要保证不存在两条轨迹相交。
在端点处(即攻击了同一个位置)也算相交,下图是一个相交的例子:
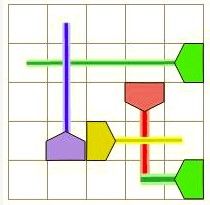
Data Constraint
20%的数据:n,m <= 5
另有20%的数据:最多有2个朝向为上或下的炮塔
另有20%的数据:最多有6个炮塔
100%的数据:1 <= n,m <= 50 , 每个位置上的敌人数量不超过999 , 保证不存在一个炮塔可以攻击另一个炮塔
Solution
我们的目的是让炮台之间的炮弹路线不相交,理所当然想到最小割。我们想一下构图。我们先找出炮台在该方向能打到的最大敌人mx,从方向为上下的炮台沿其方向相邻的点连边,从炮台连出,流量为mx-边的起点的敌人,(若(i,j)向(i+1,j)连边,流量为mx-x,割掉这条边的意义即为炮弹打到(i,j)),从方向为左右的炮台沿其方向的反方向相邻的点连边,最后连入炮台,流量为mx-边的终点的敌人,(若(i,j)向(i,j+1)连边,流量为mx-x,割掉这条边的意义即为炮弹打到(i,j+1))。为了避免下图问题: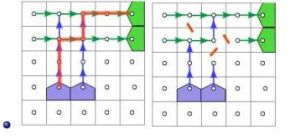
我们可以给每个点建一个横向的点和纵向的点,纵向向横向连一条+∞的边,这就保证从纵向只会又一次拐到横向。
Code
#includex=v[++i];
for (t=first[x];t;t=next[t]){
if (d[last[t]] || !value[t])continue;
v[++j]=last[t],d[last[t]]=d[x]+1;
}
}
return d[s];
}
int dg(int x,int sum){
int t,p=sum,k;
if (x==s) return sum;
for (t=first[x];t;t=next[t]){
if (!value[t]||d[last[t]]!=d[x]+1) continue;
k=dg(last[t],min(p,value[t]));
if (k){
value[t]-=k;value[dui[t]]+=k;p-=k;
if (!p) break;
}
}
if (p==sum) d[x]=-1;
return sum-p;
}
int main(){
freopen("tower.in","r",stdin);freopen("tower.out","w",stdout);
scanf("%d%d",&n,&m);s=n*m*2+1;
for (i=1;i<=n;i++)
for (j=1;j<=m;j++)
scanf("%d",&a[i][j]);
for (i=1;i<=n;i++)
for (j=1;j<=m;j++){
if (a[i][j]>=0){
x=(i-1)*m+j;
lian(x+n*m,x,maxn);lian(x,x+n*m,0);
continue;
}mx=0;
t=-a[i][j]-1;x=i+f[t][0];y=j+f[t][1];
while (x>0 && x<=n && y>0 && y<=m)mx=max(mx,a[x][y]),x+=f[t][0],y+=f[t][1];
ans+=mx;
if (a[i][j]>-3){
x=i+f[t][0];y=j+f[t][1];p=(i-1)*m+j+n*m;p1=i,q1=j;
lian(0,p,maxn);lian(p,0,0);a[p1][q1]=0;
while (x>0 && x<=n && y>0 && y<=m) k=(x-1)*m+y+n*m,lian(p,k,mx-a[p1][q1]),lian(k,p,0),p1=x,q1=y,x+=f[t][0],y+=f[t][1],p=k;
lian(p,s,mx-a[p1][q1]);lian(s,p,0);
}else{
p=(i-1)*m+j;
lian(p,s,maxn);lian(s,p,0);
if (t==3) t--;
else t++;
x+=f[t][0];y+=f[t][1];p=(x-1)*m+y;
lian(0,p,mx-max(0,a[x][y]));lian(p,0,0);
x+=f[t][0];y+=f[t][1];
while (x>0 && x<=n && y>0 && y<=m && a[x][y]>=0) k=(x-1)*m+y,lian(p,k,mx-a[x][y]),lian(k,p,0),x+=f[t][0],y+=f[t][1],p=k;
k=(x-1)*m+y,lian(p,k,mx),lian(k,p,0);
}
}
for (i=1;i<=num;i++)
if (i%2) dui[i]=i+1,dui[i+1]=i;
while (bfs()) ans-=dg(0,maxn);
printf("%d\n",ans);
}