任意多边形费马点&点群中位中心求解
点群中位中心求解
1问题讨论
从上两式不难看出,空间点(x0,y0)可以取空间中任意一点有无穷种可能,因此难以求得精确。只能使用迭代的方式来求无限逼近的解,当然求用一些奇特的方法求近似解也是可以的。
更加一般的,点群的中位中心问题是p-median问题d特例,即1-median问题。P-中值问题可以描述。而同样的问题放在多边形中,就变成了费马点的求解。
各个GIS工具软件中均有求中位中心的功能,而在matlab中也可以通过最优化函数fminsearch直接求解。本文接下来讨论点群中位中心求解的几个算法,并在matlab环境下给出其实现。本文主要从底层讨论三种算法并给出其实现,同时指出其他算法可能性。
2算法
2.1 二分互垂近似算法
基本思想为:做一组互垂的直线,两条直线均把把点群分成等数量两部分。取多组这样的直线,每组直线交点的平均中心即为点群中位中心的近似。
算法步骤为:
STEP 1: 将点群副本绕原点顺时针旋转k*90o/n,横纵两个方向,用二分法扫描点群,找到横纵方向能把点群分为两个等数量部分直线,将直线交点逆时针旋转k*90o/n,记录旋转后的点;( k指旋转的次数,初始化为0。n-1指最大旋转次数也代表着求解精度。所谓二分法就是,根据横轴或纵轴区间对半切,判断那边的点多,对多的那一边再对半切,直到切完后直线两边点的数量相等)
STEP 2: 判断k是否不大于n-1,是则k++返回STEP1,否则输出交点的平均中心。
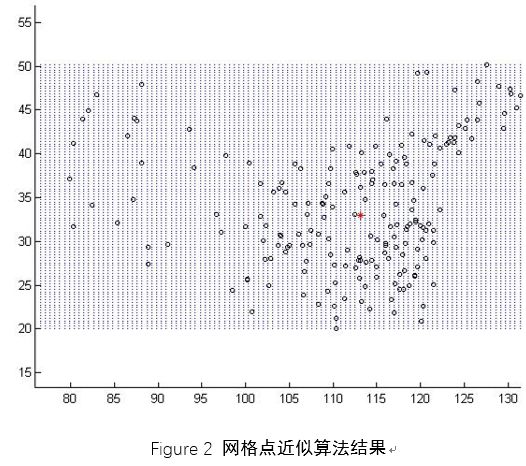
2.2 网格点近似算法
基本思想为:将点群所在的空间划分成小的网格,所有网格点中离点群总距离最近的点就是要求的点群中位中心的近似。
算法步骤为:
STEP 1: 扫描点群,找出其四至;
STEP 2: 根据输入精度n,计算点群四至矩形范围内均匀分布的格网点坐标;
STEP 3: 计算每个网格点与点群的总距离,取总距离最小的网格点作为近似的中位中心。
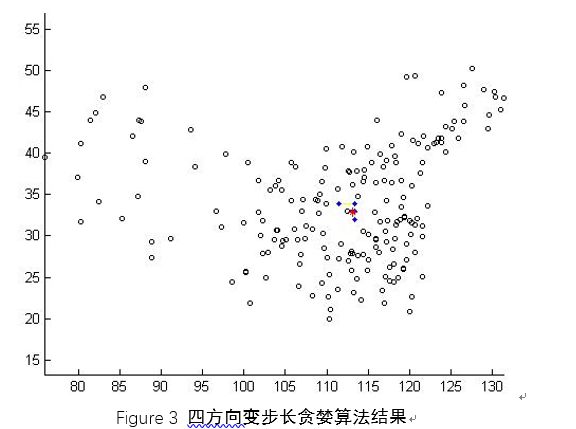
2.3 四方向变步长贪婪算法
基本原理:点群的中位中心和平均中心其实相隔的并不远,可以点群平均中心为起始点,以一定步长向四周移动,从中选择最优的点。如果当前点比所有移动点更优,说明移动的过分了,这时需要缩小步长继续移动搜索,直到精度达到要求。
算法步骤:
STEP 1:计算点群平均中心,作为起始点pt。计算点群的横纵方向的跨度,取其小者的一半作为起始步长;
STEP 2:以step为步长,向上下左右四个方向移动pt,得到pt1-4;
STEP 3:计算pt,pt1-4与点群的总距离,设总距离最小者为新的pt;
STEP 4: 判断进度是否达到要求,是则输出pt,否则继续;
STEP 5:如果当前pt与上一步pt相同,则令step=step*factor,其中factor是步长变化系数,可以取0.5等。返回第二步。
2.4 其他算法
除了上述三种算法外,此问题还可以使用模拟退火算法或牛顿迭代法进行求解。相关代码思路,在参考文献中已经给出。限于时间精力,这里不再进一步讨论。关于上述三种算法的matlab完整代码在附录中给出。3算例
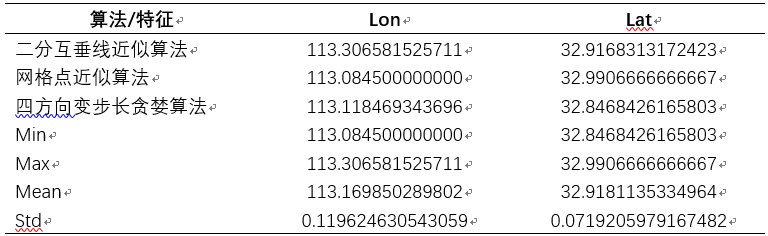
以全国300多个主要城市的经纬度坐标作为输入,利用上述三种算法分别计算,得到的结果如下图所示。各个结果的对比如下表所示,可以看出不同算法差别较小,精度较好:
参考文献
[1]Matlab选址问题[DB/OL].20170312:
http://wenku.baidu.com/link?url=38SGZiG1-LG0sIn79_OT5-b3fW8ou1hZHIH1yBVdLPv1vyfZGOGD8x7u8818ssYUb0b_DoVHYoc4I9WFYRpD9FINeDKZTQTR-FTQ1_MbfNW
[2]空间分析,郭仁忠[M].北京:高等教育出版社.p81-p82
[3]选址问题及其模型与研究[DB/OL].20170312:http://www.docin.com/p-1328378124.html
[4]白话空间统计番外篇:中位数中心算法[DB/OL].20170312:
http://blog.csdn.net/allenlu2008/article/details/47752943
[5]模拟退火求二维费马点[DB/OL].20170312:
http://www.cnblogs.com/hxsyl/archive/2013/08/12/3252773.html
[6]牛顿迭代发[DB/OL].20170312:
https://wenku.baidu.com/view/ddac681fc281e53a5902ff05.html
[7]求n个点的费马点的花式乱搞[DB/OL].20170312:
http://blog.csdn.net/wjf_wzzc/article/details/24126257
[8]二维费马点[DB/OL].20170312:http://java-mans.iteye.com/blog/1644473
附录(matlab代码实现)
%点群的中位中心计算程序,武汉大学孙一璠于20170312实现
function mediancenter= medianCenter_calcu(pts,method,isdisplay)
%主函数,用于计算点群的中位中心
%pts为输入点群[x y];
%method 为所采用的算法;
%isdisplay为逻辑值,1则显示计算过程,2不显示计算过程;
if method==1
mediancenter=in_linediv_calcu(pts,15,isdisplay);
end
if method==2
mediancenter=in_gridpt_calcu(pts,100,isdisplay);
end
if method==3
mediancenter=in_stepwise_calcu(pts,0.05,isdisplay);
end
end
function mediancenter=in_linediv_calcu(pts,n,isdisplay)
%算法1:通过互垂分割先近似求点群中位中心
%pts为输入点群,n为直线旋转次数(精度)
linepts=[0 0];resultpts=[0 0];
for k=0:n-1
pts2=in_rotate(pts,[0 0],k*pi/(2*n));
[up,bottom,left,right]=in_fideborder(pts2);
y=(up+bottom)/2;
[upnumber,downnumber]=in_calcudiv_y(pts2,y);
x=(left+right)/2;
[leftnumber,rightnumber]=in_calcudiv_x(pts2,x);
%二分法迭代求等分线,这个地方要设置一个0.05做为不再二分的条件,防止运算爆炸
while upnumber~=downnumber && abs(up-bottom)>=0.05
if upnumber>downnumber
bottom=y;
y=(up+bottom)/2;
[upnumber,downnumber]=in_calcudiv_y(pts2,y);
else
up=y;
y=(up+bottom)/2;
[upnumber,downnumber]=in_calcudiv_y(pts2,y);
end
end
while leftnumber~=rightnumber && abs(left-right)>=0.05
if leftnumber>rightnumber
right=x;
x=(left+right)/2;
[leftnumber,rightnumber]=in_calcudiv_x(pts2,x);
end
if leftnumbersteplength
pt1=[pt(1) pt(2)+step];
pt2=[pt(1)+step pt(2)];
pt3=[pt(1) pt(2)-step];
pt4=[pt(1)-step pt(2)];
searchpts=[pt;pt1;pt2;pt3;pt4];
distance=in_totaldis_calcu(pts,searchpts);
[~,index]=min(distance);
if index==1
step=step*factor;
else
pt=searchpts(index,:);
roadpts=[roadpts;pt];
end
end
mediancenter=pt;
%绘制结果与过程
if(isdisplay==true)
figure;hold on;axis equal;
plot(roadpts(:,1),roadpts(:,2),'linestyle','-','marker','.','color','y','markeredgecolor','b');
plot(pts(:,1),pts(:,2),'linestyle','none','marker','O','markersize',3,'markeredgecolor','k');
plot(mediancenter(:,1),mediancenter(:,2),'linestyle','none','marker','*','markeredgecolor','r');
end
end
function distance=in_totaldis_calcu(pts,inputpts)
%计算输入点到点群的总距离
[m,~]=size(inputpts);
distance=ones(m,1);
for i=1:m
singledis=sqrt((inputpts(i,1)-pts(:,1)).^2+(inputpts(i,2)-pts(:,2)).^2);
distance(i)=sum(singledis);
end
end
function [up,bottom,left,right]=in_fideborder(pts)
%寻找点群四至值
minvalue=min(pts);
left=minvalue(1);bottom=minvalue(2);
maxvalue=max(pts);
right=maxvalue(1);up=maxvalue(2);
end
function [upnumber,downnumber]=in_calcudiv_y(pts,y)
%计算水平线上下分别有多少个点
[m,~]=size(pts);
count=0;
for i=1:m
if pts(i,2)>=y
count=count+1;
end
end
upnumber=count;
downnumber=m-count;
end
function [leftnumber,rightnumber]=in_calcudiv_x(pts,x)
%计算竖直线左右分别有多少个点
[m,~]=size(pts);
count=0;
for i=1:m
if pts(i,1)<=x
count=count+1;
end
end
leftnumber=count;
rightnumber=m-count;
end
function pts2=in_rotate(pts,center,theta)
%将点群pts绕center点逆时针旋转theta度(弧度制)
x=pts(:,1);y=pts(:,2);
x0=center(1);y0=center(2);
x2=(x-x0).*cos(theta)-(y-y0).*sin(theta);
y2=(x-x0).*sin(theta)+(y-y0).*cos(theta);
pts2=[x2 y2];
end
function meancenter=in_meanCenter_calcu(pts)
%计算点群的平均中心
[m,~]=size(pts);
x=sum(pts(:,1))/m;
y=sum(pts(:,2))/m;
meancenter=[x y];
end