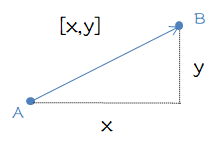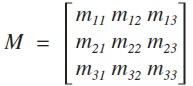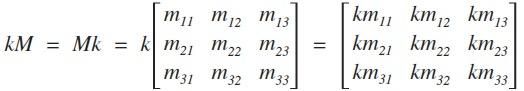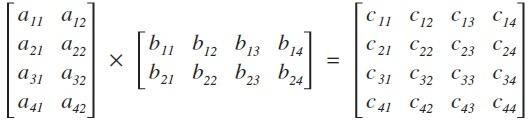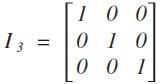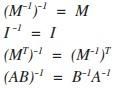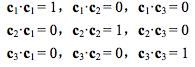Unity 3D 开发中需要掌握的数学基础知识概要整理(一)
Unity 3D 开发中需要掌握的数学基础知识概要整理(一)
目录
Unity 3D 开发中需要掌握的数学基础知识概要整理(一)
学习目的:
一、3D 数学基础知识介绍
二、Unity 中的几种常用坐标系
三、向量的基本概念
四、向量运算
五、矩阵
学习目的:
3D数学:研究在3D几何世界中的数学问题。被广泛的应用于使用计算机来模拟3D世界的领域,比如图形学,游戏,虚拟现实和动画等。
为什么要学习3D数学:掌握了3D数学的知识之后,对我们将来学习图形学、游戏制作都有很大的帮助。
一、3D 数学基础知识介绍
1、1D 数轴
1D:关于计数和度量的数学。
-
数学上,数轴是个一维的图,整数作为特殊的点均匀地分布在一条线上。数轴是一条规定了原点、方向和单位长度的直线。
![]()
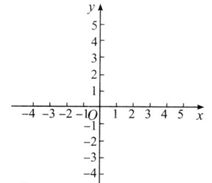
2、2D 笛卡尔坐标系
2D:关于平面的数学。
-
数学上,相交的两条直线可以确定一个唯一的平面。相交于原点的两条数轴,构成了平面放射坐标系。
-
如果两条数轴上的度量单位相等,则称此放射坐标系为笛卡尔坐标系。
-
数轴互相垂直的笛卡尔坐标系,称为笛卡尔直角坐标系,否则称为笛卡尔斜角坐标系。
-
在2D笛卡尔坐标系中,我们用(x,y)来表示一个点。称之为坐标。
-
坐标的每个分量都表明了该点与原点之间的距离和方位。每个分量都是到相应轴的有符号距离。
3、3D 空间直角坐标系
3D:关于3D空间的数学。
-
从2D扩展到3D:相对于2D笛卡尔坐标系,我们需要3个轴来表示三维坐标系,一般叫做空间直角坐标系。
-
第3个轴一般被称为z轴。一般情况下,3个轴互相垂直。
-
任意2个轴可以组成一个平面,我们一般称为XY平面,XZ平面,YZ平面,每个平面又与另一个轴相垂直。我们可以认为这3个平面是3个2D笛卡尔空间。
-
在3D中,我们用(x,y,z)来表示一个点。坐标的每个分量分别代表了该点到yz,xz,xy平面的有符号距离。
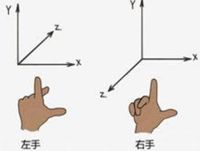
4、左手坐标系与右手坐标系
- z轴方向的确定有2种方式:左手坐标系与右手坐标系。
- 左手坐标系:伸开左手,大拇指指向X轴正方向,食指指向Y轴正方向,其他三个手指指向Z轴正方向。
- 右手坐标系:伸开右手,大拇指指向X轴正方向,食指指向Y轴正方向,其他三个手指指向Z轴正方向。
- 3D笛卡尔坐标系:右手坐标系
- OpenGL:右手坐标系
- Direct3D:左手坐标系
- Unity3D:左手坐标系(世界坐标系),即+x, +y, +z分别指向右方,上方和前方。
二、Unity 中的几种常用坐标系
1、在不同的情况下使用不同的坐标系更加方便,所以在Unity中有多种坐标系:
-
全局坐标系 World Coordinate System
a、全局坐标系是用于描述场景内所有物体位置的方向的基准,也称为世界坐标系。
b、在Unity中创建的物体都是以全局坐标系中的坐标原点(0,0,0),来确定各自的位置的。
c、可以使用transform.position来获取游戏对象的世界坐标。-
局部坐标系 Local Coordinate System
a、局部坐标系也称为模型坐标系或物体坐标系。
b、每个物体都有自身独立的物体坐标系。当物体移动或改变方向时,和该物体相关联的坐标系将随之移动或改变方向。
c、模型Mesh保存的顶点坐标均为局部坐标系下的坐标。transform.localPosition(本地坐标)可以获得物体在父物体的局部坐标系中的位置点。
父子关系,子物体以父物体的坐标点为自身的坐标原点。
如果该游戏物体没有父物体,那么transform.localPosition获得的依然是该物体在全局坐标系中的坐标。
如果该物体有父物体,则获得是在其父物体的局部坐标系中的坐标。
检视视图中显示的为localPosition的值。
-
屏幕坐标系 Screen Space
屏幕坐标系是建立在屏幕上的二维坐标系。
以像素来定义的,屏幕的左下角为(0,0),右上角为(Screen.width, Screen.height),z轴的坐标是相机的世界坐标中z轴坐标的负值。
鼠标位置坐标属于屏幕坐标,通过Input.mousePosition可以获得该位置的坐标。
手指触摸屏幕也为屏幕坐标,Input.GetTouch(0).position可以获得单个手指触摸屏幕时手指的坐标。
-
视口坐标系 ViewPort Space
视口坐标系是将Game视图的屏幕坐标系单位化,左下角(0,0),右上角(1,1)。z轴的坐标是相机的世界坐标中z轴坐标的负值。
2、坐标系之间的关联与相互转换
a.全局坐标系和局部坐标系
关联:
transform.Translate(translation:Vector3, relativeTo: Space = Space.Self);
沿着translation的方向移动|translation|的距离,其结果将应用到relativeTo坐标系中。如果relativeTo为空,则默认为局部坐标系。
转换:
Transform.TransformPoint(Vector3 position) :将一个坐标点从局部坐标系转换到全局坐标系。
Transform.InverseTransformPoint(Vector3 position):将坐标点从全局坐标系转换到局部坐标系。
Transform.TransformDirection(Vector3 direction):将一个方向从局部坐标系转换到全局坐标系。
Transform.InverseTransformDirection(Vector3 direction):将一个方向从全局坐标系转换到局部坐标系。
Transform.TransformVector(Vector3 vector):将一个向量从局部坐标系转换到全局坐标系。
Transform.InverseTransformVector(Vector3 vector):将一个向量从全局坐标系转换到局部坐标系。
其他:
Transform.forward, Transform.right, Transform.up:当前物体的物体坐标系的z轴,x轴,y轴在世界坐标系上的指向。
Vector3.forward ,(0,0,1)的缩写。在transform.Translate()中使用时,如果不表明坐标系,则为物体的局部坐标,即物体自身的正前方。
Vector3.right,(1,0,0)的缩写。
Vector3.up ,(0,1,0)的缩写。
b.屏幕坐标系与全局坐标系
转换:
Camera.ScreenToWorldPoint(Vector3 position): 将屏幕坐标转换为全局坐标。
Camera.WorldToScreenPoint(Vector3 position):将全局坐标转换为屏幕坐标。
Input.mousePosition:获得鼠标在屏幕坐标系中的坐标。
c.屏幕坐标系与视口坐标系
转换:
Camera.ScreenToViewportPoint(Vector3 position):将屏幕坐标转换为视口坐标。
Camera.ViewportToScreenPoint(Vector3 position):将视口坐标转换为屏幕坐标。
d.全局坐标系与视口坐标系
转换:
Camera.WorldToViewportPoint(Vector3 position):将全局坐标转换为视口坐标。
Camera.ViewportToWorldPoint(Vector3 position):将视口坐标转换为全局坐标。
三、向量的基本概念
1、向量的定义
-
在数学中,向量(也称为矢量),是指具有大小和方向的量。
-
向量的大小就是向量的长度,也叫做模。向量的方向描述了空间中向量的指向。
-
在数学中,书写向量时,通常用方括号将一列数括起来,如[1,2,3]。
-
水平书写的向量叫做行向量,垂直书写的向量叫做列向量。上面的向量可以书写成列向量:
 。
。 -
通常,我们用x,y来代表2D向量的分量,用x,y,z来代表3D向量的分量。
-
向量中的数表达了向量在每个维度上的有向位移。
2、点和向量的关系
-
点(Point):点中的数表示了一个位置,它没有大小、方向的概念。
-
在笛卡尔坐标系,我们可以使用2个或3个实数来表示一个点的坐标。在2D空间中,用P=(Px,Py)来表示一个点的坐标。在3D空间中,用P=(Px,Py,Pz)来表示。
-
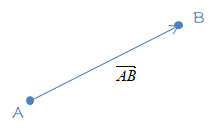
向量(Vector):向量中的数表示了向量在每个维度上的有向位移。它可以形象化地表示为带箭头的线段。箭头所指:代表向量的方向。线段长度:代表向量的大小。
-
在坐标系中,可以使用v = [x, y]来表示一个2维向量,用v = [x, y, z]来表示一个3维向量。
3、Unity中的点和向量
-
在Unity中,只有Vector2、Vector3类型,没有Point2、Point3类型。
-
Vector2类型可以用来表示2D向量和点。Vector3类型可以用来表示3D向量和点。
-
Transform.position表示一个点,即游戏物体在世界坐标系中的点。
-
Transform.forward表示一个向量,即当前物体的物体坐标系的z轴在世界坐标系上的指向。
-
在Unity中,点和向量都是以(x,y,z)的形式表示。
-
当我们想让游戏物体处于某个位置时,我们可以使用Vector3类型来表示这个点的位置坐标。
-
当我们想让游戏物体沿着某个方向以一定的速度移动时,我们可以使用Vector3类型来表示速度的向量值,即速度的大小和方向。
-
当我们想计算2个游戏物体之间的距离时,实际上计算的就是以这2个游戏物体为起点和终点的向量的长度。
四、向量运算
1、零向量
-
零向量是非常特殊的一个向量,它是唯一一个大小为0的向量,也是唯一一个没有方向的向量。
-
2D零向量表示为(0,0),3D零向量表示为(0,0,0)。
-
在Unity中,用Vector3.zero来表示3D零向量。
2、负向量
-
每个向量都有一个负向量,满足条件:一个向量和它的负向量相加等于零向量。
-
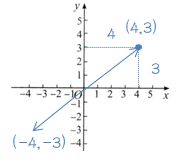
向量变负,将得到一个和原向量大小相等,方向相反的向量。
-
(2,-3,3)的负向量为(-2,3,-3)。即将向量的每个分量都变负。
3、向量的长度
-
向量的长度即向量的大小或者向量的模。
-
向量的大小就是向量各分量平方和的平方根。
-
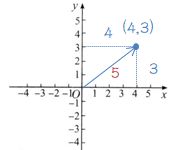
对2D向量而言,可以构造一个以该向量为斜边,以x,y分量的绝对值为直角边的直角三角形。可以根据勾股定理得到斜边的长度,即向量的长度。
-
2D向量的长度:
-
3D向量的长度:
-
在Unity中,可以通过Vector3.magnitude计算向量的长度。Vector3.sqrMagnitude则返回向量长度的平方。
-
Vector3.Distance(A,B)可以计算2个点A,B之间的距离,即返回向量AB或向量BA的长度。等同于(B-A).magnitude或(A-B).magnitude。
4、向量与标量的乘法/除法
- 向量与标量的乘法,即将向量的每个分量分别与标量相乘。
- 3D向量与标量相乘:3(1,2,3) = (3,6,9)
- 向量与非零标量的除法,即乘以该标量的倒数。
- 3D向量与标量相除:
- Unity中使用运算符*来计算与标量的乘法,用运算符/来计算与标量的除法。
5、单位向量
-
单位向量也叫做标准化向量,就是大小为1的向量。
-
在只关心向量方向,不关心向量大小时,可以使用单位向量,例如求一个面的法线向量时。
-
对任意的非零向量,我们都可以计算出它的单位向量,即将其归一化(normalization)。
-
向量的归一化:求得向量的长度后,用向量除以它的长度。
-
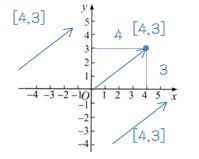
(4,3)归一化后的单位向量为:
-
在Unity中,可以使用Vector3.Normalize来归一化向量。使用Vector3.normalized来获得归一化后的单位向量。
6、矢量的点积
代码中用dot(a, b)来表示。
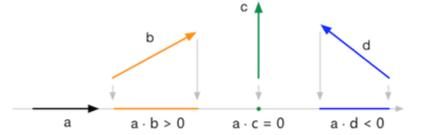
点积的几何意义
点积几乎用到了图形学的各个方面,其中一个就是投影。有一个单位矢量a和长度不限的矢量b。那么a与b的点积就是b在a方向上的有符号的投影。投影的结果是有符号的,如下图:
如果a不是单位矢量,那么a与b的点积等同于b在a上的投影,再乘以a的长度。
点积的几种数学公式:
下面要重点介绍点积的另一种表达式:
推导很容易,这里不加介绍。从这个公式可以看出两个向量的夹角对于点积结果的影响,小于90度为正,等于90度为0,大于90度为负。还可以用反余弦求出两个向量的夹角。
7、矢量的叉积
相信上学时都学过,这里直接上公式:
注意:
叉积的几何意义:
两个矢量叉积会得到一个同时垂直于这两个矢量的新矢量
我们知道两个方向互不平行的矢量可以确定一个平面,所以叉积最常见的应用就是计算垂直于一个平面的矢量,我们后面会在顶点法线,切线那里用到。
五、矩阵
矢量可以看成是nx1的列矩阵或1xn的行矩阵,其中n对应了矢量的维度。把矢量和矩阵联系在一起是为了让矢量像矩阵一样一起参与矩阵运算。这在空间变换中非常有用。
1)矩阵的运算
矩阵和标量的乘法:
矩阵和矩阵的乘法:
假设矩阵A的大小是4x2,B的大小是2x4,计算C = A x B,则C的大小是4x4。
其中:
![]()
也就是对应的行乘以对应的列。
矩阵乘法的一些表达式:
2)特殊矩阵
a、方块矩阵
简称方阵,就是行和列相等的矩阵。如果在方阵中除了对角线上的元素其他元素都是0,则成为对角矩阵。
b、单位矩阵
对角线元素都是1的对角矩阵就是单位矩阵。用 I 来表示。例如3x3的单位矩阵如下:
MI = IM = M
c、转置矩阵
![]()
d、逆矩阵
不是所有的矩阵都有逆矩阵,比如零矩阵,首先该矩阵必须是个方阵。M的逆矩阵表示为,它们满足一个公式:
![]()
如果一个矩阵有逆矩阵,我们就说它是可逆的或者非奇异的,相反则是不可逆的或奇异的。
逆矩阵的公式:
这里有个逆矩阵的几何意义,矩阵是可以表示变换的,逆矩阵则可以还原这个变换。比如用矩阵M对向量v进行了一次变换,如果我们想还原回v,只需要对变换结果乘以M的逆矩阵,公式如下:
![]()
f、正交矩阵
如果矩阵M和它的转置矩阵的乘积是单位矩阵的话,矩阵M就是正交的,公式为:
![]()
所以和上面的逆矩阵相比,我们发现:
![]()
这个公式很有用,因为求解一个矩阵的逆矩阵计算量很大,但转置矩阵很容易,所以如果我们知道该矩阵是正交矩阵,那用转置矩阵就可以当逆矩阵了。那如何判断一个矩阵是正交矩阵呢。用计算公式求解当然可以,但同样很麻烦,让我们看看它的几何意义。根据正交矩阵的定义,我们有:
我们可以把(![]() )当成M每一行和M转置每一列的向量,所以就有了等式:
)当成M每一行和M转置每一列的向量,所以就有了等式:
(1)![]() 和自己点积的时候都为1,还记得向量和自己点积等于其模的平方的公式吧,不记得就再看看上面,模的平方为1,那模就是1,所以它们都是单位矩阵。
和自己点积的时候都为1,还记得向量和自己点积等于其模的平方的公式吧,不记得就再看看上面,模的平方为1,那模就是1,所以它们都是单位矩阵。
(2)它们之间两两点积都得0,说明它们互相都垂直。
而这两个规律对每一列同样适用,因为M是正交矩阵,其转置也是正交矩阵。这两个规律说明什么,又是单位向量,又是彼此垂直,这不就是我上面提到的标准正交基吗。所以我们得出结论,正交矩阵的行与行之间,列与列之间分别构成了一组标准正交基。
这在空间转换中很有用,如果这些基矢量是一组标准正交基的话,那我们就可以直接用其转置矩阵来得到其逆矩阵了。
3)行矩阵还是列矩阵
我们都知道,向量是可以作为行矩阵或列矩阵的,本身没有区别,但和矩阵相乘就有区别了,因为我们要用到各种空间转换会用到向量与矩阵相乘。比如v代表的1x3的向量和M代表的3x3的矩阵相乘,如果vM那结果是1x3的矩阵,如果Mv(v变成列矩阵),那结果就是3x3的矩阵。我们往往需要的是后者,所以在Unity中,常规做法是把矢量放在矩阵的右边,即Mv。例如:
CBAv = (C(B(Av)))
表示先对v使用A变换,再用B变换,再用C变换,是从右往左的顺序。所以如无特殊情况,我们往往使用向量的列矩阵表达式。