题目描述
Sylvia 是一个热爱学习的女♂孩子。
前段时间,Sylvia 参加了学校的军训。众所周知,军训的时候需要站方阵。
Sylvia 所在的方阵中有n \times mn×m名学生,方阵的行数为 nn,列数为 mm。
为了便于管理,教官在训练开始时,按照从前到后,从左到右的顺序给方阵中 的学生从 1 到 n \times mn×m 编上了号码(参见后面的样例)。即:初始时,第 ii 行第 jj 列 的学生的编号是(i-1)\times m + j(i−1)×m+j。
然而在练习方阵的时候,经常会有学生因为各种各样的事情需要离队。在一天 中,一共发生了 qq件这样的离队事件。每一次离队事件可以用数对(x,y) (1 \le x \le n, 1 \le y \le m)(x,y)(1≤x≤n,1≤y≤m)描述,表示第 xx 行第 yy 列的学生离队。
在有学生离队后,队伍中出现了一个空位。为了队伍的整齐,教官会依次下达 这样的两条指令:
-
向左看齐。这时第一列保持不动,所有学生向左填补空缺。不难发现在这条 指令之后,空位在第 xx 行第 mm列。
- 向前看齐。这时第一行保持不动,所有学生向前填补空缺。不难发现在这条 指令之后,空位在第 nn 行第 mm列。
教官规定不能有两个或更多学生同时离队。即在前一个离队的学生归队之后, 下一个学生才能离队。因此在每一个离队的学生要归队时,队伍中有且仅有第 nn 行 第 mm 列一个空位,这时这个学生会自然地填补到这个位置。
因为站方阵真的很无聊,所以 Sylvia 想要计算每一次离队事件中,离队的同学 的编号是多少。
注意:每一个同学的编号不会随着离队事件的发生而改变,在发生离队事件后 方阵中同学的编号可能是乱序的。
输入输出格式
输入格式:
输入共 q+1q+1 行。
第 1 行包含 3 个用空格分隔的正整数 n, m, qn,m,q,表示方阵大小是 nn 行 mm 列,一共发 生了 qq 次事件。
接下来 qq 行按照事件发生顺序描述了 qq 件事件。每一行是两个整数 x, yx,y,用一个空 格分隔,表示这个离队事件中离队的学生当时排在第 xx 行第 yy 列。
输出格式:
按照事件输入的顺序,每一个事件输出一行一个整数,表示这个离队事件中离队学 生的编号。
输入输出样例
2 2 3 1 1 2 2 1 2
1 1 4
说明
【输入输出样例 1 说明】
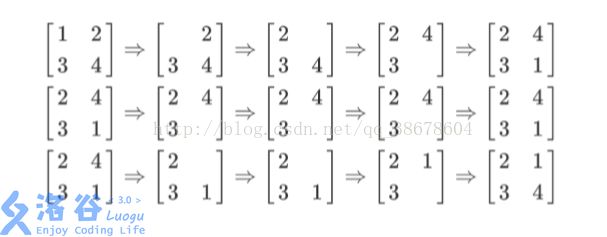
列队的过程如上图所示,每一行描述了一个事件。 在第一个事件中,编号为 1 的同学离队,这时空位在第一行第一列。接着所有同学 向左标齐,这时编号为 2 的同学向左移动一步,空位移动到第一行第二列。然后所有同 学向上标齐,这时编号为 4 的同学向上一步,这时空位移动到第二行第二列。最后编号 为 1 的同学返回填补到空位中。
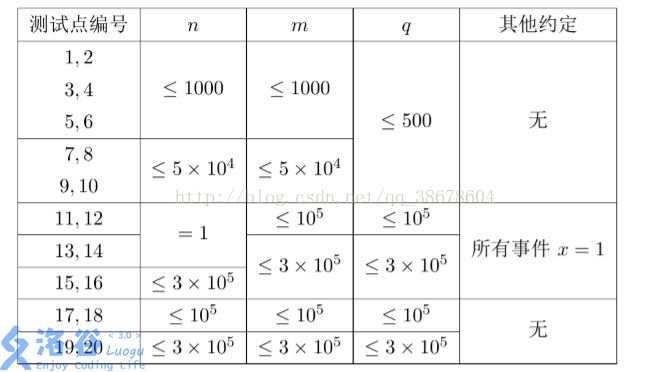
【数据规模与约定】
数据保证每一个事件满足 1 \le x \le n,1 \le y \le m1≤x≤n,1≤y≤m
题解
NOIP2017最后一道题,考试40min时就写到了,可以说心情澎湃。。【然而并没有想到正解】
看到部分分很多,考场拿了部分分
前50分:
前50分q很小,用O(q^2)倒推就好了
把之前的出队位置记下来,若当前询问位置为(x,y),上一次出队位置为(x1,y1)
若(x,y) == (n,m),说明是刚入队,那么就转移到上次出队位置(x1,y1)
假若y == m且x1 <= x,说明在上次一队形调整中(x,y)是由(x,y + 1)移动过来的,那么y++
假若x == n且y1 <= y,同理可以退出上一次在(x + 1,y),那么x++
最后就会推回原来的位置
30分x=1
100分
#include
#include
#include
#include
#include
#define LL long long int
#define REP(i,n) for (int i = 1; i <= (n); i++)
using namespace std;
const int maxn = 600005,maxm = 20000005,INF = 1000000000;
inline int read(){
int out = 0,flag = 1;char c = getchar();
while (c < 48 || c > 57) {if (c == '-') flag = -1; c = getchar();}
while (c >= 48 && c <= 57) {out = out * 10 + c - 48; c = getchar();}
return out * flag;
}
int n,m,q,Max;
vector G[maxn];
struct node{int sum,ls,rs; node() {ls = rs = 0;} }e[maxm];
int siz = 0,rt[maxn],pos;
void modify(int& u,int l,int r){
if (!u) u = ++siz; e[u].sum++;
if(l < r) {
int mid = l + r >> 1;
if (mid >= pos) modify(e[u].ls,l,mid);
else modify(e[u].rs,mid + 1,r);
}
}
int Query(int u,int l,int r,int k){
if (l == r) return l;
int mid = l + r >> 1,sizl = mid - l + 1 - e[e[u].ls].sum;
if (sizl >= k) return Query(e[u].ls,l,mid,k);
else return Query(e[u].rs,mid + 1,r,k - sizl);
}
LL Del_r(int x,LL v){
pos = Query(rt[n + 1],1,Max,x); modify(rt[n + 1],1,Max);
LL ans = pos <= n ? 1ll * pos * m: G[n + 1][pos - n - 1];
G[n + 1].push_back(v ? v : ans);
return ans;
}
LL Del_l(int x,int y){
pos = Query(rt[x],1,Max,y); modify(rt[x],1,Max);
LL ans = pos < m ? 1ll * (x - 1) * m + pos : G[x][pos - m];
G[x].push_back(Del_r(x,ans));
return ans;
}
int main()
{
int x,y;
n = read(); m = read(); q = read(); Max = max(m,n) + q;
while (q--){
x = read(); y = read();
if (y == m) printf("%lld\n",Del_r(x,0));
else printf("%lld\n",Del_l(x,y));
}
return 0;
}