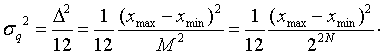通信原理day7：第三章：抽样；均匀量化；非均匀量化；A律；增量（ΔM）调制

该章节在整个通信系统中解决的问题：
模拟信号的数字化

模拟信号的数字化通常包括抽样、量化和编码三个过程。
抽样将时间连续，幅值连续的信号变换为时间离散，幅值连续的信号，以便于量化处理；
量化把幅值连续的信号变换为幅值离散的信号。量化结束后要接着编码调制（PCM/ΔM）
编码则是将量化后的数字信号用某种二进制的码组来表示。

本章要求：
1.知道每种编码调制方式的具体调制方法，知道其信噪比的计算公式

1.抽样定理

对信号以f_s的频率抽样后，系统的信息速率/比特率R_b=Nf_s
其频谱相当于原来的频谱以f_s平移

1.1低通信号的抽样定理

抽样频率 ：ω_s≥2ω_H
本质：原信号在频域上频移ωs而不产生混叠时，ωs所满足的条件

注：语音信号上限3.4kHz

1.2带通信号的抽样定理

带宽：W=ω_H-ω_L
N=ω_H/W的整数部分
M=ω_H/W-N
抽样频率 ：ω_s=2W(1+M/N)

2.量化

量化分为均匀量化和非均匀量化，均匀量化，因此更常用非均匀量化。

信号的平均功率S_x ：

衡量量化的优劣常用量化信噪比来表示。
量化信噪比SNR_q：

2.1 均匀量化

2.1.1.抽样频率，传输速率

PCM系统的抽样频率满足低通信号的抽样定理。

因此PCM系统的传输速率为R_b=Nf_s

2.1.2.量化位数，量化电平，量化间隔

量化位数N
量化区间数(量化电平) M

信号x(t)的幅度取值范围 [xmin,xmax]
量化间隔Δ：

2.1.3.量化噪声，量化信噪比

量化噪声：

当信号x(t)的幅度取值在[-Vp,Vp]范围内均匀分布，则有
均匀量化的量化噪声：

平均功率

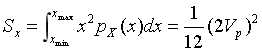
因此线性PCM编码的均匀量化信噪比

由此可见，均匀量化的量化噪声与信号功率无关，它适用于动态范围小的信号。均匀量化每增加一位量化精度，量化信噪比SNR_q,dB 将有约6dB的提升。但量化信噪比的改善是以增加带宽为代价的。

2.2 非均匀量化

非均匀量化的基本思想是根据信号幅度所处的不同区间来确定量化间隔的大小。

非均匀量化的目的是提高小信号的量化信噪比，代价是减小大信号的量化信噪比。

非均匀量化的优点是：改善小信号的量化信噪比，降低编码的位数；缺点是：实现相对复杂。

非均匀量化通常这样实现：
（1）对模拟信号进行某种非线性变换 y=f(x)(压缩变换)
（2）对变换后的信号y进行均匀量化得到y_k
在对信号y_k进行还原时，再对信号进行相反的变换x_k=f^-1(y_k)（扩张变换）

设量化器的压缩变换特性为y=f(x)
则 量化噪声

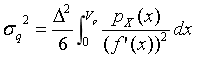
当压缩特性为对数函数时，信噪比SNR_q成为与p_X(x)无关的常数

两种常用的非均匀量化方式：A律和μ律。μ律不常考，我国采用A律，因此主要了解A律PCM编码

3. A律脉冲编码调制(PCM)：

A律输出码组为M₁M₂M₃M₄M₅M₆M₇M₈共八位
M₁：极性码
M₂M₃M₄：段落码（8段0~7。除了第0段是0 ~ 32，第k段的起始电平为2^k×16）
M₅M₆M₇M₈：段内码（16段0~15，段内电平均匀分布，段内特性斜率相同，并进行均匀量化，线性编码）

---

已知A律PCM编码器，输入信号的动态范围为-Vp≤x≤Vp，若抽样获得的信号值为x0则：
编码输出码组：
M₁：
x₀是正数–>M₁=1
x₀是负数–>M₁=0

M₂M₃M₄：

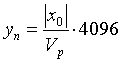
2^k×16 ≤ y_n ≤ 2^k+1×16，因此处在第k线段内，M₂M₃M₄=k

M₅M₆M₇M₈：

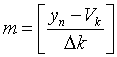
这里是指m取整数值。Δk是第k段的段内电平，Δk=2^k。V_k是第k段的起始电平，V_k=2^k×16

对应的十三位线性PCM码b₁₂b₁₁b₁₀b₉b₈b₇b₆b₅b₄b₃b₂b₁b₀：
M₁：
M₁=1–>b₁₂=1
M₁=0–>b₁₂=0

M₂M₃M₄：
除了第0段是从b₅=0开始以外，处在第k段线段内，则
b_k+4=1

M₅M₆M₇M₈：
b_k+3b_k+2b_k+1b_k+0=M₅M₆M₇M₈
b_k-1=1，然后再后面的b码全部写成“ * ”

根据编码输出码组得到信号值时，过程类似。

---

4.增量（ΔM）调制

4.1 不发生斜率过载的条件

输入信号为x(t)，抽样频率fs，量化台阶Δ，增量调制不发生过载的条件：

4.2 量化台阶/输入信号的振幅，抽样频率

若输入信号为m(t)=Asinω0t，为避免过载噪声，增量调制DM编码器能够正常工作的输入信号的振幅应满足

由此可得，ΔM系统的抽样频率满足

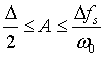
4.3 量化信噪比

量化信噪比：
输入信号频率为f，接收端低通滤波器的截止频率fH，系统的抽样频率为fs，在输入正弦信号，且临界振幅的情况下，系统则得到最大量化信噪比

当输入正弦信号，振幅A小于临界振幅A_max时，其量化信噪比

补充：数字压扩自适应增量调制：

ΔM调制主要受到两类噪声的影响，即基本量化噪声与过载量化噪声。减少这两种噪声的措施却是互相矛盾的。增加量化阶距的幅度可以对陡峭变化的波型有更好的跟踪效果，但较大的量化阶距势必会增加量化噪声。如果希望在减少过载噪声的同时不增加量化噪声，就需要在波形陡峭变化时用较大的量化阶距，而在波形相对平坦时用较小的量化阶距。这就是自适应增量调制的基本概念。当信号变化比较平缓时，相应的量化阶距取较小值Δ₁，因此有较小的量化噪声；若检测到连续3个连“1”或连“0”，系统将自动地调整到较大的量化阶距Δ₂，从而避免过载失真的情况出现。