二维数组的多种排序方法（数据结构实验）

某个二维数组存放了一系列的字符串，试利用排序的一些算法（请利用不少于两种算法实现排序，如插入、冒泡、快速排序、堆排序等）对这些字符串按照字典顺序进行排序。

例如：二维数组的字符串如下：

char  s[][20]={“while”，”if”，“else”，”do”，“for”，”switch”，“case”};

本人使用了直接插入排序、快速排序以及堆排序三种算法对二维数组进行排序；

下面的代码在VS2019上获得通过！

如果想要在Dev-C++ 上运行，把_s类函数修改下在加些头文件就可以啦

我将每种排序的每一步都写了出来，方便查验

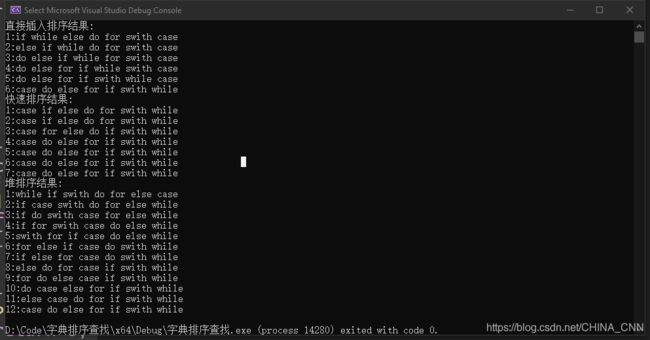
效果如图：

代码如下：

// 字典排序查找.cpp : This file contains the 'main' function. Program execution begins and ends there.
//
#include 
#include
#include
#include 
using namespace std;

void Print_IS(char a[][20], int n, int i) {
	printf("%d:", i);
	for (int j = 0; j < n; j++) {
		cout << a[j] << " ";
	}
	printf("\n");
}
void Insert_sort(char S[][20], int n) {
	int j;
	char x[20];
	for (int i = 1; i < n; i++) {
		if (strcmp(S[i], S[i - 1]) < 0) {//strcmp函数，用于字符串大小比较，这一步是初次比较
			j = i - 1;
			strcpy_s(x, 20, S[i]);//strcpy_s用于赋值，并且保证是安全的。
			while (j > -1 && strcmp(x, S[j]) < 0) {//当位置合法并且相邻两数仍然没有顺序时
				strcpy_s(S[j + 1], 20, S[j]);//将较小值不停向前挪动
				j--;
			}
			strcpy_s(S[j + 1], 20, x);//最后一步的j多减了1，所以最后放置的时候再加回来
		}
		Print_IS(S, n, i);//按需打印函数，可实现每一步的过程输出
	}
}
void Print_QS(char a[][20], int n, int i) {
	printf("%d:", i);
	for (int j = 1; j < n; j++) {
		cout << a[j] << " ";
	}
	printf("\n");
}
int k;
int Quick_sort(char S[][20],int start,int end) {
	int i, j;
	i = start;
	j = end;
	
	strcpy_s(S[0], 20, S[start]);
	while (i < j) {//当i指针始终小于j时
		while (i < j && strcmp(S[0], S[j]) < 0)//并且基轴始终比j要比较的值小
		{
			j--;
		}
		if (i < j) {//当i不小于j或者基轴比j要比较的值大时
			strcpy_s(S[i], 20, S[j]);//
			i++;
		}
		while (i= 0; i--)
	{
		if ((2 * i + 1) < len && strcmp(heap[i], heap[2 * i + 1]) < 0)    /* 根节点大于左子树 */
		{
			strcpy_s(temp,20, heap[i]);
			strcpy_s(heap[i],20, heap[2 * i + 1]);
			strcpy_s(heap[2 * i + 1],20, temp);
			/* 检查交换后的左子树是否满足大顶堆性质 如果不满足 则重新调整子树结构 */
			j=Print_Heap(heap, 7, ++q);
			if ((2 * (2 * i + 1) + 1 < len && strcmp(heap[2 * i + 1], heap[2 * (2 * i + 1) + 1] ) < 0)
				|| (2 * (2 * i + 1) + 2 < len && heap[2 * i + 1] < heap[2 * (2 * i + 1) + 2]))
			{
				MaxHeap_sort(heap, len);
			}
		}
		if ((2 * i + 2) < len && strcmp(heap[i], heap[2 * i + 2]) < 0)    /* 根节点大于右子树 */
		{
			strcpy_s(temp, 20,heap[i]);
			strcpy_s(heap[i],20, heap[2 * i + 2]);
			strcpy_s(heap[2 * i + 2],20, temp);
			j=Print_Heap(heap, 7, ++q);
			/* 检查交换后的右子树是否满足大顶堆性质 如果不满足 则重新调整子树结构 */
			if ((2 * (2 * i + 2) + 1 < len && strcmp(heap[2 * i + 2], heap[2 * (2 * i + 2) + 1]) < 0)
				|| (2 * (2 * i + 2) + 2 < len && strcmp(heap[2 * i + 2], heap[2 * (2 * i + 2) + 2]) < 0))
			{
				MaxHeap_sort(heap, len);
			}
		}
	}
}
/* Function: 交换交换根节点和数组末尾元素的值*/
void Swap(char heap[][20], int len)
{
	char temp[20];
	strcpy_s(temp,20, heap[0]);
	strcpy_s(heap[0],20, heap[len - 1]);
	strcpy_s(heap[len - 1],20, temp);
}
int main()
{
	char s[][20] =
	{
		"while",
		"if",
		"else",
		"do",
		"for",
		"swith",
		"case"
	};
	int i = 0;
	cout << "直接插入排序结果:" << endl;
	Insert_sort(s, 7);//插入排序！

	char S[][20] =
	{
		"TestWordUseless",
		"while",
		"if",
		"else",
		"do",
		"for",
		"swith",
		"case"
	};
	cout << "快速排序结果:" << endl;
	Quick_sort(S, 1, 7);
	char H[][20] =
	{
		"while",
		"if",
		"else",
		"do",
		"for",
		"swith",
		"case"
	};
	cout << "堆排序结果:" << endl;
	int len;
	len = 7;
	for (i = len; i > 0; i--)
	{
		MaxHeap_sort(H, i);
		Swap(H, i);
	}
	Print_Heap(H, 7, j+1);
	return 0;
}