CS231n课程作业(一) kNN classifier
之前就写过一个简单的kNN分类器:机器学习之kNN算法,kNN的理论非常通俗易懂,有兴趣的可以参考。
cs231n是针对图像的,本次作业内容是对图像进行分类。
分类的标准就是待分类图像与训练集图像的L2距离。
(PS:样本集是32x32x3的图像,所以分类前需要对待分类图像进行resize。但其实没有人用kNN进行图像识别,所以不用care,hahaha)
源代码见GitHub:CS231n-assignment1-kNN
注:主要结合源码理解
一、数据集描述
数据集:CIFAR-10
类别数:10类
训练集:50000张,图片为 32x32x3。后取5000张
测试集:10000张,后取500张。
类标签:0,1,2,…,9
处理:将单张图片reshape为(1,3072),这样一行为一个样本,便于后续计算
example:

二、求训练集与测试集的L2距离
X_test: (500,3072) , y_test: (500,)
X_train: (5000,3072) , y_train: (5000,)
得到的距离矩阵dists: (500,5000), 其中每个元素均代表测试样本与训练样本的L2距离
1. 单循环:
def compute_distances_one_loop(self, X):
"""
Compute the distance between each test point in X and each training point
in self.X_train using a single loop over the test data.
Inputs:
- X: A numpy array of shape (num_test, D) containing test data.
Returns:
- dists: A numpy array of shape (num_test, num_train) where dists[i, j]
is the Euclidean distance between the ith test point and the jth training
point.
"""
num_test = X.shape[0] #测试集数量:500
num_train = self.X_train.shape[0] #训练集数量: 5000
dists = np.zeros((num_test, num_train)) #距离矩阵: (500,5000)
temp = []
for i in range(num_test):
#######################################################################
# TODO: #
# Compute the l2 distance between the ith test point and all training #
# points, and store the result in dists[i, :]. #
#######################################################################
s = ((X[i] - self.X_train)**2) # 5000x3072
s = s.sum(axis = 1) #按行求和
s = np.sqrt(s)
temp.append(s)
dists = np.mat(temp) #将列表转为矩阵 np.mat()
#######################################################################
# END OF YOUR CODE #
#######################################################################
return dists2. 无循环
无循环比较牛,借鉴网上大佬的。实质是(a-c)**2展开,其中b = 2*a*c.
可以在草稿纸画一画。无循环运算起来非常高效率。
我个人觉得应该掌握!算法的优化还是很重要的!!!
def compute_distances_no_loops(self, X):
"""
Compute the distance between each test point in X and each training point
in self.X_train using no explicit loops.
Input / Output: Same as compute_distances_two_loops
"""
num_test = X.shape[0]
num_train = self.X_train.shape[0]
dists = np.zeros((num_test, num_train))
#########################################################################
# TODO: #
# Compute the l2 distance between all test points and all training #
# points without using any explicit loops, and store the result in #
# dists. #
# #
# You should implement this function using only basic array operations; #
# in particular you should not use functions from scipy. #
# #
# HINT: Try to formulate the l2 distance using matrix multiplication #
# and two broadcast sums. #
#########################################################################
c = np.sum(np.square(self.X_train),axis = 1)
b = -2 * np.dot(X,self.X_train.T)
a = np.transpose([np.sum(np.square(X),axis = 1)])
dists = np.sqrt(a + b + c)
#########################################################################
# END OF YOUR CODE #
#########################################################################
return dists————————————————-2018-1-5更新——————————————–
3. 使用sicpy计算矩阵间L2距离
from scipy.spatial.distance import cdist
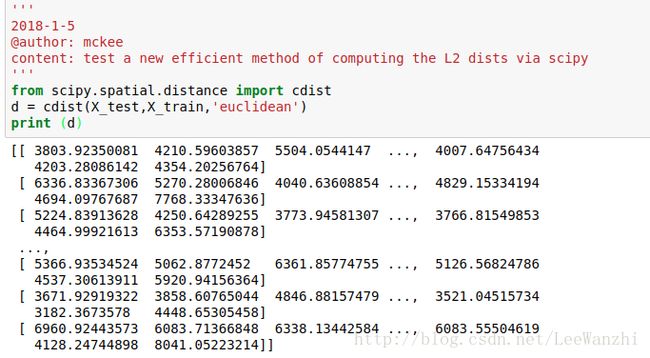
d = cdist(X_test,X_train,'euclidean')
print (d)结果和前面一样:
————————————————-更新完毕—————————————————–
三、计算测试集的预测类别
L2距离得到后,即可对每个测试样本选择k个最近的距离,得到它们的类别,然后再用majority_vote来预测测试样本的类别,为后面计算精度做准备。
def predict_labels(self, dists, k=1):
"""
Given a matrix of distances between test points and training points,
predict a label for each test point.
Inputs:
- dists: A numpy array of shape (num_test, num_train) where dists[i, j]
gives the distance betwen the ith test point and the jth training point.
Returns:
- y: A numpy array of shape (num_test,) containing predicted labels for the
test data, where y[i] is the predicted label for the test point X[i].
"""
num_test = dists.shape[0] #测试集的数量
y_pred = np.zeros(num_test) #对应的类标签
index = dists.argsort() #按元素从小到大的顺序,依次列出该元素的角标[重要]
for i in range(num_test):
# A list of length k storing the labels of the k nearest neighbors to
# the ith test point.
#########################################################################
# TODO: #
# Use the distance matrix to find the k nearest neighbors of the ith #
# testing point, and use self.y_train to find the labels of these #
# neighbors. Store these labels in closest_y. #
# Hint: Look up the function numpy.argsort. #
#########################################################################
closest_y = []
buf = np.asarray(index[i,:])[0] #将矩阵变为数组
closest_y = self.y_train[buf][:k] #取最相邻的k个标签
#########################################################################
# TODO: #
# Now that you have found the labels of the k nearest neighbors, you #
# need to find the most common label in the list closest_y of labels. #
# Store this label in y_pred[i]. Break ties by choosing the smaller #
# label. #
#########################################################################
count = np.bincount(closest_y) #统计0到closest_y中最大元素,分别出现的个数;结果为list
y_pred[i] = np.argmax(count) #返回list中最大数的角标,此时对应类标签
#########################################################################
# END OF YOUR CODE #
#########################################################################
return y_pred四、评定精度
from cs231n.classifiers import KNearestNeighbor
K = 10
kNN = KNearestNeighbor()
kNN.train(X_train, y_train)
#print (X_train.shape)
#print (X_test.shape)
dist_no_loop = kNN.compute_distances_no_loops(X_test)
dist = np.mat(dist_no_loop)
y_test_pred = kNN.predict_labels(dist, k=K)
#y_test_pred = classifier.predict(X_test, k=20)
# Compute and display the accuracy
num_correct = np.sum(y_test_pred == y_test) #统计预测值与实际值相同的个数,其实我之前是不知道这样处理的,所以我要记住这种处理方法!!
accuracy = float(num_correct) / num_test #计算精度
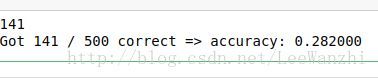
print (num_correct)
print('Got %d / %d correct => accuracy: %f' % (num_correct, num_test, accuracy))kNN主要的过程就在上面了,完整的过程需要结合源码学习。源码在文章开头已经给出。
五、涉及到的numpy重要函数
因为我平时只是用的时候才会去查,写kNN的时候发现很多函数很实用,所以记录下来。
1. flatnonzero(array == a)
功能:找到array中值等于a的元素的位置
eg:
for y in range(10):
idxs = np.flatnonzero(y_train == y)
print idxs
2. np.random.choice(array, num, replace = False)
功能:从array中随机选出num个样本,且不允许有重复值
eg: np.random.choice(idxs, samples_per_class, replace=False)
3. reshape(row,-1) , reshape(-1,column)
功能: 将array按行数为row排
将array按列数为column排
4.np.tile(array,(a,b))
功能:将array整体复制成a行b列
eg:np.tile(X_test[i],(X_train.shape[0],1))
这样X_test[i]即为5000行,3072列
注意:在矩阵减去同一行数组的情况下,不必使用这个函数,直接相减即可。
5. np.mat(array)、np.asarray(matrix)
功能:将数组转为矩阵,将矩阵转为数组
6. array.argsort()
功能:按元素从小到大的顺序,依次列出该元素的角标
eg: dists.argsort()

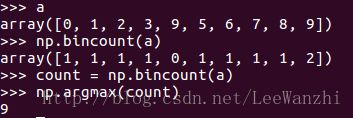
7.np.bincount(array)
功能:统计0到array中最大元素分别出现的个数;结果为list
eg:

8.np.argmax(array), np.argmin(array)与之类似
功能:统计array中最大元素出现的位置
9.np.array_split(array,num)
功能:将array分成num份,返回的是一个列表,一个位置对应一份
六、交叉验证(cross validation)
基本思想:Split up the training data into folds, where one fold works as validation set and the others work as training data. cycle through the choice of which fold is the validation set and store all accuracies. Then find out the best value of hyperparameters, such as the value of k.
So, cross-validation is used to tune hyperparameters.