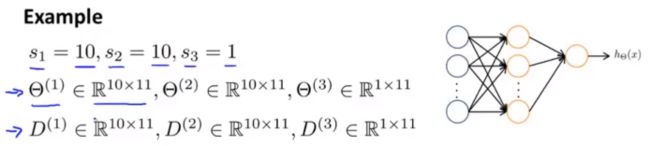【机器学习】神经网络 II
本文为机器学习的学习总结,讲解神经网络。欢迎交流
代价函数
下图是一个神经网络的多元分类问题:
其中训练集为 { ( x ( 1 ) , y ( 1 ) ) , … , ( x ( m ) , y ( m ) ) } \{(x^{(1)},y^{(1)}),…,(x^{(m)},y^{(m)})\} {(x(1),y(1)),…,(x(m),y(m))}, L L L 为网络的总层数, s l s_l sl 为第 l l l 层的单元数,其中不包括偏差单元。
神经网络有两种分类问题,一种是二元分类,另一种是多元分类。
在二元分类中, y = 0 , 1 y=0,1 y=0,1,输出 h Θ ( x ) ∈ R h_\Theta(x)\in \mathbb{R} hΘ(x)∈R, s L = 1 s_L=1 sL=1 即网络输出单元的个数为 1,为了简化表示,我们设输出单元的个数 K = 1 K=1 K=1。
多元分类问题中,假设有 K K K 类,则输出为 K K K 维列向量, s L = K , ( k ≥ 3 ) s_L=K,\quad (k\ge3) sL=K,(k≥3)。
逻辑回归模型的代价函数为:
J ( θ ) = − 1 m [ ∑ i = 1 m ( y ( i ) log h θ ( x ( i ) ) + ( 1 − y ( i ) ) log ( 1 − h θ ( x ( i ) ) ) ] + λ 2 m ∑ j = 1 n θ j 2 J(\theta)=-\frac{1}{m}[\sum\limits_{i=1}^m(y^{(i)}\log h_\theta(x^{(i)})+(1-y^{(i)})\log(1-h_\theta(x^{(i)}))]+\frac{\lambda}{2m}\sum\limits_{j=1}^n\theta_j^2 J(θ)=−m1[i=1∑m(y(i)loghθ(x(i))+(1−y(i))log(1−hθ(x(i)))]+2mλj=1∑nθj2
这里不再是逻辑回归的一个输出单元,而是 k k k 个:
J ( θ ) = − 1 m [ ∑ i = 1 m ∑ k = 1 K ( y k ( i ) log ( h θ ( x ( i ) ) ) k + ( 1 − y k ( i ) ) log ( 1 − ( h θ ( x ( i ) ) ) k ) ] J(\theta)=-\frac{1}{m}[\sum\limits_{i=1}^m\sum\limits_{k=1}^K(y^{(i)}_k\log (h_\theta(x^{(i)}))_k+(1-y^{(i)}_k)\log(1-(h_\theta(x^{(i)}))_k)] J(θ)=−m1[i=1∑mk=1∑K(yk(i)log(hθ(x(i)))k+(1−yk(i))log(1−(hθ(x(i)))k)]
+ λ 2 m ∑ l = 1 L ∑ i = 1 s l ∑ j = 1 s l + 1 ( Θ j i ( l ) ) 2 +\frac{\lambda}{2m}\sum\limits_{l=1}^L\sum\limits_{i=1}^{s_l}\sum\limits_{j=1}^{s_l+1}(\Theta_{ji}^{(l)})^2 +2mλl=1∑Li=1∑slj=1∑sl+1(Θji(l))2
此时 h Θ ( x ) ∈ R K , ( h Θ ( x ) ) i = i t h o u t p u t h_\Theta(x)\in \mathbb{R}^K,(h_\Theta(x))_i=i^{th} output hΘ(x)∈RK,(hΘ(x))i=ithoutput, Θ j i ( l ) \Theta_{ji}^{(l)} Θji(l) 表示第 l − 1 l-1 l−1 层的第 j j j 个神经元与第 l l l 层的第 i i i 个神经元之间的权值(参数)。上式的意义为先将 K K K 个输出单元的逻辑回归的代价函数相加。
反向传播算法
现在我们要找到参数 Θ \Theta Θ 从而最小化 J ( Θ ) J(\Theta) J(Θ)。为使用梯度下降法或其他高级优化算法,我们需要写一个函数,输入参数 Θ \Theta Θ 并计算 J ( Θ ) J(\Theta) J(Θ) 和偏导项 ∂ ∂ Θ i j ( l ) J ( Θ ) \frac{\partial}{\partial\Theta_{ij}^{(l)}}J(\Theta) ∂Θij(l)∂J(Θ)。计算 J ( Θ ) J(\Theta) J(Θ) 可以用代价函数的公式,我们在这里讲解如何计算偏导项。
为简单起见,我们从训练集只有一个样本讲解。
假设我们有一个样本值 ( x , y ) (x,y) (x,y),首先使用前向传播来计算在给定输入的时候假设函数的输出结果:
a ( 1 ) = x a^{(1)}=x a(1)=x
z ( 2 ) = Θ ( 1 ) a ( 1 ) z^{(2)}=\Theta^{(1)}a^{(1)} z(2)=Θ(1)a(1)
a ( 2 ) = g ( z ( 2 ) ) ( + a 0 ( 2 ) ) a^{(2)}=g(z^{(2)})(+ a_0^{(2)}) a(2)=g(z(2))(+a0(2))
z ( 3 ) = Θ ( 2 ) a ( 2 ) z^{(3)}=\Theta^{(2)}a^{(2)} z(3)=Θ(2)a(2)
a ( 3 ) = g ( z ( 3 ) ) ( + a 0 ( 3 ) ) a^{(3)}=g(z^{(3)})(+ a_0^{(3)}) a(3)=g(z(3))(+a0(3))
z ( 4 ) = Θ ( 3 ) a ( 3 ) z^{(4)}=\Theta^{(3)}a^{(3)} z(4)=Θ(3)a(3)
a ( 4 ) = h Θ ( x ) = g ( z ( 4 ) ) a^{(4)}=h_\Theta(x)=g(z^{(4)}) a(4)=hΘ(x)=g(z(4))
我们实现了将前向传播向量化,使得我们可以计算神经网络中所有神经元的激活值。接下来我们使用反向传播算法来计算偏导项。
反向传播算法就是对每一个结点计算 δ j ( l ) \delta_j^{(l)} δj(l),代表第 l l l 层的第 j j j 个结点的激活值误差。我们以上面的 4 层神经网络架构举例,这里 L = 4 L=4 L=4。
δ j ( 4 ) = a j ( 4 ) − y j , a ( 4 ) = h Θ ( x ) \delta_j^{(4)}=a^{(4)}_j-y_j,\quad a^{(4)}=h_\Theta(x) δj(4)=aj(4)−yj,a(4)=hΘ(x)
写成向量化的形式,其中每一项代表一个向量,维数是输出神经元的数量:
δ ( 4 ) = a ( 4 ) − y \delta^{(4)}=a^{(4)}-y δ(4)=a(4)−y
继续计算前面几层的误差项 δ \delta δ:
δ ( 3 ) = ( Θ ( 3 ) ) T δ ( 4 ) . ∗ g ′ ( z ( 3 ) ) \delta^{(3)}=(\Theta^{(3)})^T\delta^{(4)}.*g'(z^{(3)}) δ(3)=(Θ(3))Tδ(4).∗g′(z(3))
其中 . ∗ .* .∗ 为 Matlab 中的点乘,即矩阵元素对应相乘,而不是矩阵相乘。其中 g ′ ( z ( 3 ) ) = a ( 3 ) . ∗ ( 1 − a ( 3 ) ) g'(z^{(3)})=a^{(3)}.*(1-a^{(3)}) g′(z(3))=a(3).∗(1−a(3))。同样:
δ ( 2 ) = ( Θ ( 2 ) ) T δ ( 3 ) . ∗ g ′ ( z ( 2 ) ) , g ′ ( z ( 2 ) ) = a ( 2 ) . ∗ ( 1 − a ( 2 ) ) \delta^{(2)}=(\Theta^{(2)})^T\delta^{(3)}.*g'(z^{(2)}),\quad g'(z^{(2)})=a^{(2)}.*(1-a^{(2)}) δ(2)=(Θ(2))Tδ(3).∗g′(z(2)),g′(z(2))=a(2).∗(1−a(2))
这里没有 δ ( 1 ) \delta^{(1)} δ(1),因为输入层不会有误差。反向传播的意思就是将最后一层的误差向前传播。这样我们就能求解出偏导项:
∂ ∂ Θ i j ( l ) J ( Θ ) = a j ( l ) δ i ( l + 1 ) \frac{\partial}{\partial\Theta_{ij}^{(l)}}J(\Theta)=a^{(l)}_j\delta_i^{(l+1)} ∂Θij(l)∂J(Θ)=aj(l)δi(l+1)
这里忽略了正则项。
通过一个样本值的过渡,应该对反向传播算法有一定的理解了,我们给出反向传播算法的伪代码。
假设我们有 m m m 个训练样本 { ( x ( 1 ) , y ( 1 ) ) , … , ( x ( m ) , y ( m ) ) } \{(x^{(1)},y^{(1)}),…,(x^{(m)},y^{(m)})\} {(x(1),y(1)),…,(x(m),y(m))},需要设 Δ i j ( l ) = 0 \Delta_{ij}^{(l)}=0 Δij(l)=0,用来计算偏导项 ∂ ∂ Θ i j ( l ) J ( Θ ) \frac{\partial}{\partial\Theta_{ij}^{(l)}}J(\Theta) ∂Θij(l)∂J(Θ)。
-
遍历所有样本:
for i = 1 to m,设 a ( 1 ) = x ( i ) a^{(1)}=x^{(i)} a(1)=x(i),然后用正向传播计算出后面每层的激活值 a ( l ) a^{(l)} a(l)。 -
计算误差项 δ ( L ) = a ( L ) − y ( L ) \delta^{(L)}=a^{(L)}-y^{(L)} δ(L)=a(L)−y(L),再根据反向传播算法逐个计算每一层的误差项。
-
用 Δ \Delta Δ 来积累前面计算过的偏导数项, Δ i j ( l ) : = Δ i j ( l ) + a j ( l ) δ i ( l + 1 ) \Delta_{ij}^{(l)}:=\Delta_{ij}^{(l)}+a^{(l)}_j\delta_i^{(l+1)} Δij(l):=Δij(l)+aj(l)δi(l+1),写成向量形式为 Δ ( l ) : = Δ ( l ) + δ ( l + 1 ) ( a ( l ) ) T \Delta^{(l)}:=\Delta^{(l)}+\delta^{(l+1)}(a^{(l)})^T Δ(l):=Δ(l)+δ(l+1)(a(l))T。
然后跳出循环执行,当 j = 0 j=0 j=0 时无标准化项:
D i j ( l ) : = 1 m Δ i j ( l ) + λ Θ i j ( l ) j ≠ 0 D_{ij}^{(l)}:=\frac{1}{m}\Delta_{ij}^{(l)}+\lambda\Theta_{ij}^{(l)}\qquad j≠0 Dij(l):=m1Δij(l)+λΘij(l)j=0
D i j ( l ) : = 1 m Δ i j ( l ) j = 0 D_{ij}^{(l)}:=\frac{1}{m}\Delta_{ij}^{(l)}\qquad j=0 Dij(l):=m1Δij(l)j=0
最后可以证明 ∂ ∂ Θ i j ( l ) J ( Θ ) = D i j ( l ) \frac{\partial}{\partial\Theta_{ij}^{(l)}}J(\Theta)=D_{ij}^{(l)} ∂Θij(l)∂J(Θ)=Dij(l)。我们就可以用梯度下降算法或高级优化算法最小化代价函数了。
理解反向传播算法
反向传播算法是神经网络的基础,因此对前面推到步骤的理解是很重要的。接下来我们用手动计算过程来加深对反向传播算法的理解。
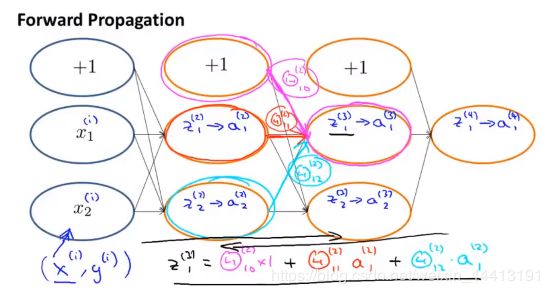
首先我们给出这样一个神经网络架构,利用前向传播计算出每个神经元的激活值:
而反向传播与正向传播过程十分相似,只是从右到左方向相反。
回顾有一个输出单元的神经网络的代价函数:
J ( θ ) = − 1 m [ ∑ i = 1 m ( y ( i ) log h θ ( x ( i ) ) + ( 1 − y ( i ) ) log ( 1 − h θ ( x ( i ) ) ) ] + λ 2 m ∑ j = 1 n θ j 2 J(\theta)=-\frac{1}{m}[\sum\limits_{i=1}^m(y^{(i)}\log h_\theta(x^{(i)})+(1-y^{(i)})\log(1-h_\theta(x^{(i)}))]+\frac{\lambda}{2m}\sum\limits_{j=1}^n\theta_j^2 J(θ)=−m1[i=1∑m(y(i)loghθ(x(i))+(1−y(i))log(1−hθ(x(i)))]+2mλj=1∑nθj2
对于同一组样本,我们同时使用了前向传播和反向传播。当只有一个输出神经元时, y ( i ) ∈ R y^{(i)}\in \mathbb{R} y(i)∈R,我们忽略正则化,第 i i i 个样本的代价函数可表示为:
c o s t ( i ) = y ( i ) log h θ ( x ( i ) ) + ( 1 − y ( i ) ) log ( 1 − h θ ( x ( i ) ) ) cost(i)=y^{(i)}\log h_\theta(x^{(i)})+(1-y^{(i)})\log(1-h_\theta(x^{(i)})) cost(i)=y(i)loghθ(x(i))+(1−y(i))log(1−hθ(x(i)))
我们可以把上式当作神经网络的输出值与实际值的方差,表示预测的准确性。
接着再看反向传播算法。直观的感受是我们在计算每一层的 δ ( l ) \delta^{(l)} δ(l),即每层神经元激活值的误差。实际上, δ j ( l ) = ∂ ∂ z j ( l ) c o s t ( i ) \delta_j^{(l)}=\frac{\partial}{\partial z_j^{(l)}}cost(i) δj(l)=∂zj(l)∂cost(i),改变 z j ( l ) z_j^{(l)} zj(l) 会改变神经网络的输出值。 δ j ( l ) \delta_j^{(l)} δj(l) 为代价函数关于计算的中间项的偏导数,其衡量的是,为了影响这些中间项,我们想要改变神经网络中的权值的程度,进而影响神经网络的输出值,并影响所有的代价函数。
反向传播算法的过程如下:
举例说明, δ 2 ( 2 ) = Θ 12 ( 2 ) δ 1 ( 3 ) + Θ 22 ( 2 ) δ 2 ( 3 ) \delta_2^{(2)}=\Theta_{12}^{(2)}\delta_1^{(3)}+\Theta_{22}^{(2)}\delta_2^{(3)} δ2(2)=Θ12(2)δ1(3)+Θ22(2)δ2(3),可以看出其计算过程与正向传播十分相似。这些 δ \delta δ 值只关于隐藏单元,并不包括偏置单元,这取决于对反向传播的定义以及算法的实现。偏执单元的输出总为 +1,通常会计算出它们的值,但并不使用,因为其并不影响偏导数的计算。
参数展开
梯度下降算法和高级优化算法通常要求将输入的参数为长向量,这需要我们将参数矩阵展开为向量。具体来说,当我们写一个函数,传入参数 theta 计算出代价值 jVal 和梯度向量 gradient,然后将函数 costFunction 和初始参数值 initialTheta 传入优化函数 fminunc 中。这里参数 theta 和梯度值 gradient 为 n n n 或 n + 1 n+1 n+1 维的向量。
function [jVal, gradient] = costFunction(theta);
...
optTheta = fminunc(@costFunction, initialTheta, options);
在逻辑回归中这部分没有任何问题,但在神经网络中,我们的参数不再是向量而是矩阵。我们将参数矩阵 Θ 1 , Θ 2 , Θ 3 \Theta_1,\Theta_2,\Theta_3 Θ1,Θ2,Θ3 设为 Theta1, Theta2, Theta3,将 D ( 1 ) , D ( 2 ) , D ( 3 ) D^{(1)},D^{(2)},D^{(3)} D(1),D(2),D(3) 设为 D1, D2, D3,然后展开成向量,以便将它们转换成恰当的格式传入。
例如我们有一个神经网络架构:
在 Matlab 中,我们用下面的命令在矩阵和向量之间相互转换:
% 取出所有的Theta,然后全部展开
thetaVec = [Theta1(:); Theta2(:); Theta3(:);];
DVec = [D1(:); D2(:); D3(:);]
从向量返回到矩阵表达:
% 取出thetaVec的前10×11个元素
Theta1 = reshape(thetaVec(1:110), 10, 11);
Theta2 = reshape(thetaVec(111:220), 10, 11);
Theta3 = reshape(thetaVec(221:231), 1, 11);
下面在 Matlab 中进行演示。
>> Theta1 = ones(10,11);
>> Theta2 = 2*ones(10,11);
>> Theta3 = 3*ones(1,11);
% 矩阵展开为向量
>> thetaVec = [Theta1(:); Theta2(:); Theta3(:)];
>> size(thetaVec)
ans = 231 1
% 向量恢复为矩阵
>> reshape(thetaVec(1:110),10,11)
ans =
列 1 至 10
1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
列 11
1
1
1
1
1
1
1
1
1
1
>> reshape(thetaVec(111:220),10,11);
>> reshape(thetaVec(221:231),1,11);
下面将这个方法应用于我们的学习算法。
假设我们有初始参数值 Θ ( 1 ) , Θ ( 2 ) , Θ ( 3 ) \Theta^{(1)},\Theta^{(2)},\Theta^{(3)} Θ(1),Θ(2),Θ(3),将其展开为长向量作为 initialTheta 传入优化函数 fminunc。
然后是实现代价函数。代价函数得到长向量格式的输入参数 thetaVec,在函数中用 reshape 重组得到参数矩阵 Θ ( 1 ) , Θ ( 2 ) , Θ ( 3 ) \Theta^{(1)},\Theta^{(2)},\Theta^{(3)} Θ(1),Θ(2),Θ(3),然后进行前向传播和反向传播来计算出代价函数和导数。最后取出导数值然后展开得到 gradientVec 并返回。
使用矩阵表达式的好处是在进行正向和反向传播时会更加方便,容易充分利用向量化实现;而向量的优点是一些高级优化函数通常需要传入参数为长向量。
梯度检验
在反向传播中,有很多较难实现的细节,并且很容易产生 bug,当其与梯度下降等算法共同使用时,看起来能够正常运行,并且代价函数在每次迭代时都会下降,但最后得到的神经网络的误差比正确值高一个数量级,并且我们并不知道结果是由 bug 导致的。而梯度检测可以解决所有这一类问题,在每次运用神经网络或其他复杂模型实现反向传播或类似梯度下降算法时,最好都做梯度检验,这完全保证我们的正向和反向传播都是 100% 正确的。而这种 bug 的出现通常与反向传播实现的错误有关。
下图是 J ( Θ ) J(\Theta) J(Θ) 的函数图像, Θ \Theta Θ 处的导数斜率(蓝色直线)可以近似为双侧差分的斜率(红色直线):
双侧差分: ∂ ∂ Θ J ( Θ ) ≈ J ( Θ + ϵ ) − J ( Θ − ϵ ) 2 ϵ \frac{\partial}{\partial\Theta}J(\Theta)≈\frac{J(\Theta+\epsilon)-J(\Theta-\epsilon)}{2\epsilon} ∂Θ∂J(Θ)≈2ϵJ(Θ+ϵ)−J(Θ−ϵ)。如果 ϵ \epsilon ϵ 足够小,双侧差分就是导数值,但选定的 ϵ \epsilon ϵ 过小会引发很多数值问题。通常取 ϵ = 1 0 − 4 \epsilon=10^{-4} ϵ=10−4 这种很小的数字。还有一种单侧差分的形式:
∂ ∂ Θ J ( Θ ) ≈ J ( Θ + ϵ ) − J ( Θ ) ϵ \frac{\partial}{\partial\Theta}J(\Theta)≈\frac{J(\Theta+\epsilon)-J(\Theta)}{\epsilon} ∂Θ∂J(Θ)≈ϵJ(Θ+ϵ)−J(Θ)
双侧差分更准确。可以用下面的代码计算出双侧差分:
gradeApprox = (J(theta + EPSILON) - J(theta + EPSILON)) / (2*EPSILON);
当 Θ \Theta Θ 是一个 n n n 维向量时,用类似的思想可以估计所有的偏导数项:
∂ ∂ Θ 1 J ( Θ ) ≈ J ( Θ 1 + ϵ , . . . , Θ n ) − J ( Θ 1 − ϵ , . . . , Θ n ) 2 ϵ \frac{\partial}{\partial\Theta_1}J(\Theta)≈\frac{J(\Theta_1+\epsilon,...,\Theta_n)-J(\Theta_1-\epsilon,...,\Theta_n)}{2\epsilon} ∂Θ1∂J(Θ)≈2ϵJ(Θ1+ϵ,...,Θn)−J(Θ1−ϵ,...,Θn)
⋮ \vdots ⋮
∂ ∂ Θ n J ( Θ ) ≈ J ( Θ 1 , . . . , Θ n + ϵ ) − J ( Θ 1 , . . . , Θ n − ϵ ) 2 ϵ \frac{\partial}{\partial\Theta_n}J(\Theta)≈\frac{J(\Theta_1,...,\Theta_n+\epsilon)-J(\Theta_1,...,\Theta_n-\epsilon)}{2\epsilon} ∂Θn∂J(Θ)≈2ϵJ(Θ1,...,Θn+ϵ)−J(Θ1,...,Θn−ϵ)
在 Matlab 中,为了估算导数所要实现的代码:
for i = 1:n,
thetaPlus = theta;
% 给theta中的一项+epsilon
thetaPlus(i) = thetaPlus(i) + EPSILON;
thetaMinus = theta;
% 给theta中的一项-epsilon
thetaMinus(i) = thetaMinus(i) + EPSILON;
gradeApprox = (J(thetaPlus) - J(thetaMinus)) / (2*EPSILON);
end;
将结果与反向传播中得到的导数对比,检查 gradeApprox 与 DVec 是否在数值上近似。
我们总结一下反向神经网络的实现步骤:
- 通过反向传播计算
DVec - 计算出
gradeApprox进行数值上的梯度检验 - 在训练网络前要关掉梯度检验,因为梯度检验中导数的计算量很大,十分耗时,比反向传播过程慢很多
随机初始化
当执行梯度下降或其他高级优化算法时,我们需要传入参数 Θ \Theta Θ 的初始值。在逻辑回归中,我们将参数设为全 0,但在神经网络中,这种错误会导致对称权重问题:
在上图中,蓝色线的权重相等都为 0,红色和绿色同样。意味着第二层的激活值都是由相同的假设函数计算的,对于所有的样本都有 a 1 ( 2 ) = a 2 ( 2 ) a^{(2)}_1=a^{(2)}_2 a1(2)=a2(2),进而 δ 1 ( 2 ) = δ 2 ( 2 ) \delta^{(2)}_1=\delta^{(2)}_2 δ1(2)=δ2(2),偏导数满足 ∂ ∂ Θ 01 J ( Θ ) = ∂ ∂ Θ 02 J ( Θ ) \frac{\partial}{\partial\Theta_{01}}J(\Theta)=\frac{\partial}{\partial\Theta_{02}}J(\Theta) ∂Θ01∂J(Θ)=∂Θ02∂J(Θ)。这意味着在每次梯度下降时,参数值被更新为学习率×导数值,更新后的参数值仍然相等 Θ 01 ( 1 ) = Θ 02 ( 1 ) \Theta_{01}^{(1)}=\Theta_{02}^{(1)} Θ01(1)=Θ02(1),则权重仍然相等,再执行梯度下降算法依然相等。
当有很多隐藏单元时,所有的单元都计算相同的假设函数,造成高度冗余现象,意味着最后的逻辑回归单元只能得到一个特征,因为所有的单元都一样。
因此我们在初始化的时候要使用随机初始化的思想,以解决上面的对称权重问题。对于每个 Θ \Theta Θ 初始化为 [ − ϵ , ϵ ] [-\epsilon,\epsilon] [−ϵ,ϵ] 区间的一个随机值,其中 ϵ \epsilon ϵ 与梯度检验无关。对应代码为:
% rand()随机生成元素在0到1之间的矩阵
Theta1 = rand(10,11)*(2*INIT_EPSILON) - INIT_EPSILON;
Theta2 = rand(1,11)*(2*INIT_EPSILON) - INIT_EPSILON;
总结
选择神经网络架构
选择神经网络架构具有一定的原则,我们将输入神经元个数设为特征 x ( i ) x^{(i)} x(i) 的维度,输出神经元个数设为分类的类别个数。
在多元分类问题中,注意要将输出 y y y 写为向量的形式,而不是一个实数。
对于隐藏层的选择,我们通常只使用一个隐藏层,如果选择多个隐藏层,我们通常将每个隐藏层神经元的个数选为相同的值。通常情况下,隐藏单元越多越好,但是不可避免地会带来很大的计算量。对于每个隐藏层中神经元数量,应该和输入的 x x x 的维度匹配,通常等于 x x x 的维度或是其整数倍。
这些原则会得到更好的模型结构。在后面讲到神经网络的运用时,我们会更详细的进行讲解。
训练神经网络的步骤
- 构建神经网络,随机初始化权重
- 使用前向传播得到每个输入的 h Θ ( x ) h_\Theta(x) hΘ(x)
- 通过代码计算代价函数 J ( Θ ) J(\Theta) J(Θ)
- 使用反向传播算法计算偏导数项 ∂ ∂ Θ j k J ( Θ ) \frac{\partial}{\partial\Theta_{jk}}J(\Theta) ∂Θjk∂J(Θ)。计算偏导也可以用更高级的算法来代替 for 循环。
- 进行梯度检查。检查后关闭梯度检查
- 使用一个最优化算法,与反向传播算法结合,将代价函数和偏导项作为参数传入最优化算法。
我们在这里详细讲解一下梯度下降算法在神经网络中的应用。
神经网络的代价函数是非凸的,但在神经网络中使用最优化算法,代价函数通常会下降到一个较低的值,并不影响我们训练神经网络。
为方便绘图,我们假设神经网络中只有 2 个参数:
在最低点时,对于大多数的样本,假设函数的输出与样本实际结果相差很小。在这里,梯度下降算法的思想是,从某个随机的地方开始不停下降,由反向传播算法计算出梯度下降的方向,最终到达局部最优解。我们试图找到最优的参数值使得神经网络的输出值与训练集观测到的 y ( i ) y^{(i)} y(i) 实际值尽可能接近。