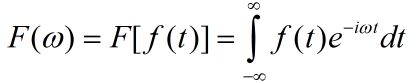傅里叶变换原理讲解及python手动实现
创作不易,如果对您有所帮助,请帮忙点赞,感谢!
一. 傅里叶变换简介:
在数字图像处理中,有两个经典的变换被广泛使用——傅里叶变换和霍夫变换。傅里叶变换是将时间域上的信号转变为频率域上的信号,进而进行图像去噪、图像增强等处理。
傅里叶变换(Fourier Transform,FT)后,对同一事物的观看角度随之改变,可以从频域里发现一些从时域里不易察觉的特征。某些在时域内不好处理的地方,在频域内可以容易地处理。
傅里叶定理:“ 任何连续周期信号都可以表示成(或者无限逼近)一系列正弦信号的叠加。”
一维傅里叶公式如下:
w 表示频率, t 表示时间, 它将频率域的函数表示为时间域函数 f(t)的积分 ↑
我们知道,灰度图像是由二维的离散的点构成的。二维离散傅里叶变换(Two-Dimensional Discrete Fourier Transform)常用于图像处理中,对图像进行傅里叶变换后得到其频谱图。频谱图中频率高低表征图像中灰度变化的剧烈程度。图像中边缘和噪声往往是高频信号,而图像背景往往是低频信号。我们在频率域内可以很方便地对图像的高频或低频信息进行操作,完成图像去噪,图像增强,图像边缘提取等操作。
对二维图像进行傅里叶变换用如下式子进行:
图像长M,高N。F(u,v)表示频域图像,f(x,y)表示时域图像。u的范围为[0,M-1],v的范围为[0,N-1] ↑
对二维图像进行傅里叶逆变换式子如下:
![]()
图像长M,高N。f(x,y)表示时域图像, F(u,v)表示频域图像。x的范围为[0,M-1],y的范围为[0,N-1] ↑
二. python实现二维图像的傅里叶变换原理
import cv2
import numpy as np
# DFT
def dft(img):
H, W, channel = img.shape
# Prepare DFT coefficient
G = np.zeros((H, W, channel), dtype=np.complex)
# prepare processed index corresponding to original image positions
x = np.tile(np.arange(W), (H, 1))
y = np.arange(H).repeat(W).reshape(H, -1)
# dft
for c in range(channel):
for v in range(H):
for u in range(W):
G[v, u, c] = np.sum(img[..., c] * np.exp(-2j * np.pi * (x * u / W + y * v / H))) / np.sqrt(H * W)
return G
# IDFT
def idft(G):
# prepare out image
H, W, channel = G.shape
out = np.zeros((H, W, channel), dtype=np.float32)
# prepare processed index corresponding to original image positions
x = np.tile(np.arange(W), (H, 1))
y = np.arange(H).repeat(W).reshape(H, -1)
# idft
for c in range(channel):
for v in range(H):
for u in range(W):
out[v, u, c] = np.abs(np.sum(G[..., c] * np.exp(2j * np.pi * (x * u / W + y * v / H)))) / np.sqrt(W * H)
# clipping
out = np.clip(out, 0, 255)
out = out.astype(np.uint8)
return out
# Read image
img = cv2.imread("../head.png").astype(np.float32)
# DFT
G = dft(img)
# write poser spectal to image
ps = (np.abs(G) / np.abs(G).max() * 255).astype(np.uint8)
cv2.imwrite("out_ps.jpg", ps)
# IDFT
out = idft(G)
# Save result
cv2.imshow("result", out)
cv2.imwrite("out.jpg", out)
cv2.waitKey(0)
cv2.destroyAllWindows()
三. 实验结果:
原图 ↑
经过傅里叶变换、反变换后的图像 ↑
四. C语言实现图像傅里叶变换:
// 傅里叶变换
void fre_spectrum(short **in_array, short **out_array, long height, long width)
{
double re, im, temp;
int move;
for (int i = 0; i < height; i++){
for (int j = 0; j < width; j++){
re = 0;
im = 0;
for (int x = 0; x < height; x++){
for (int y = 0; y < width; y++){
temp = (double)i * x / (double)height +
(double)j * y / (double)width;
move = (x + y) % 2 == 0 ? 1 : -1;
re += in_array[x][y] * cos(-2 * pi * temp) * move;
im += in_array[x][y] * sin(-2 * pi * temp) * move;
}
}
out_array[i][j] = (short)(sqrt(re*re + im*im) / sqrt(width*height));
if (out_array[i][j] > 0xff)
out_array[i][j] = 0xff;
else if (out_array[i][j] < 0)
out_array[i][j] = 0;
}
}
}
// 傅里叶反变换
void idft(double** re_array, double** im_array, short** out_array, long height, long width)
{
double real, temp;
for (int i = 0; i < height; i++){
for (int j = 0; j < width; j++){
real = 0;
for (int x = 0; x < height; x++){
for (int y = 0; y < width; y++){
temp = (double)i * x / (double)height +
(double)j * y / (double)width;
real += re_array[x][y] * cos(2 * pi * temp) -
im_array[x][y] * sin(2 * pi * temp);
}
}
out_array[i][j] = (short)(real / sqrt(width*height));
if (out_array[i][j] > 0xff)
out_array[i][j] = 0xff;
else if (out_array[i][j] < 0)
out_array[i][j] = 0;
}
}
printf("idft done\n");
}五. 参考内容:
https://www.cnblogs.com/wojianxin/p/12529809.html
https://www.jianshu.com/p/835a7a68d0ee
六. 版权声明:
未经作者允许,请勿随意转载抄袭,抄袭情节严重者,作者将考虑追究其法律责任,创作不易,感谢您的理解和配合!