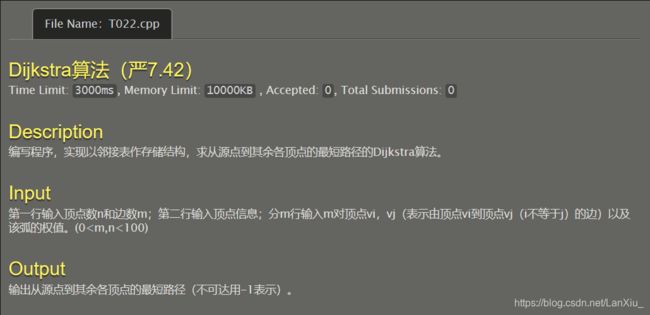
『西工大-数据结构-NOJ』 022-Dijkstra算法(耿7.42) 『西北工业大学』

解题思路：

这道题要求使用邻接来作为储存结构，使用Dijkstra算法计算源点到其余各点的最短距离，无法到达时令距离为-1.
了解一下Dijkstra算法：



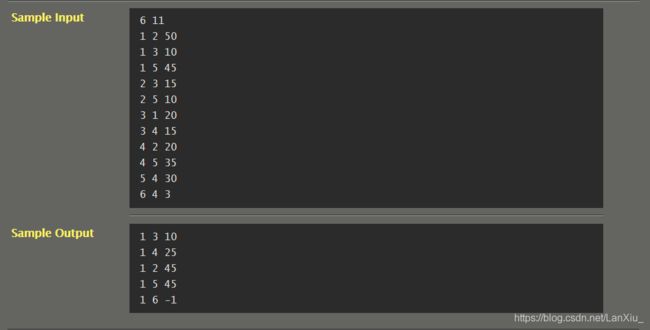
而根据题目预期的Output来看，输出数据是按照最短路径升序输出的，因此我们还要对数据进行一次排序，最短路径升序优先，其次是目标点序号，之后将最短路径为-1的放在最后输出。
具体操作见代码，代码中有部分注释。

题解代码：

#include
#include

#define MAX 200
#define NUMMAX 10000
#define FALSE 0
#define TRUE 1

typedef struct EdgeNode{
    int endvex;//相邻顶点字段
    int weight;//边的权
    struct EdgeNode *nextedge;//链字段
}EdgeList;//边表

typedef struct{
    int vertex;//顶点信息
    EdgeList *edgelist;//边表头指针
}VexNode;//顶点表

typedef struct{
    VexNode vexs[MAX];
    int vexNum,edgeNum;//图的顶点和边个数
}GraphList;

typedef struct path{
    int visited[MAX];
    int pathweight[MAX];
}Path;

void CreatGraphList(GraphList *G, int n, int m){
    G->vexNum = n;
    G->edgeNum = m;
    for(int i=0;i<n;i++){
        G->vexs[i].vertex = i+1;
        G->vexs[i].edgelist = NULL;
    }
    int v1,v2,w;
    for(int j=0;j<m;j++){
        scanf("%d %d %d",&v1,&v2,&w);
        EdgeList *g = (EdgeList*)malloc(sizeof(EdgeList));
        g->endvex = v2-1;
        g->weight = w;
        g->nextedge = G->vexs[v1-1].edgelist;
        G->vexs[v1-1].edgelist = g;
    }
}

void InitPath(GraphList *G, Path *P){//初始化
    for(int i=0;i<G->vexNum;i++){
        P->visited[i] = -1;
        P->pathweight[i] = 0;
    }
    EdgeList *p;
    p = G->vexs[0].edgelist;
    while(p){
        P->visited[p->endvex] = 1;
        P->pathweight[p->endvex] = p->weight;
        p = p->nextedge;
    }
}

int CanMove(GraphList *G, Path *P){
    for(int i=1;i<G->vexNum;i++){
        if(P->visited[i]==1){
            return TRUE;
        }
    }
    return FALSE;
}

int FindMinPath(GraphList *G, Path *P){
    int min=NUMMAX,minPathNum=-1;
    for(int i=1;i<G->vexNum;i++){
        if (P->visited[i]==1){
            if (P->pathweight[i]<min){
                min = P->pathweight[i];
                minPathNum = i;
            }
        }
    }
    return minPathNum;
}

void UpdatePath(GraphList *G, Path *P, int minPathNum){
    EdgeList *p;
    int minPath = P->pathweight[minPathNum];
    p = G->vexs[minPathNum].edgelist;
    P->visited[minPathNum] = 0;
    while(p){
    if(P->visited[p->endvex]==1){
        if(p->weight+minPath<P->pathweight[p->endvex]){
                P->pathweight[p->endvex] = p->weight+minPath;
        }
    }
    else{
        if(P->visited[p->endvex]==-1){
                P->visited[p->endvex]=1;
                P->pathweight[p->endvex] = p->weight+minPath;
            }
        }
        p = p->nextedge;
    }
}

void QuickSort(int array1[], int array2[], int maxlen, int begin, int end){
    int i,j;
    if(begin<end){
        i=begin + 1;
        j=end;
        while(i<j){
            if(array1[i]>array1[begin]){
                int temp;
                temp = array1[i];
                array1[i] = array1[j];
                array1[j] = temp;
                temp = array2[i];
                array2[i] = array2[j];
                array2[j] = temp;
                j--;
            }
            else{
                i++;
            }
        }
        if(array1[i]>=array1[begin]){
            i--;
        }
        int temp;
        temp = array1[begin];
        array1[begin] = array1[i];
        array1[i] = temp;
        temp = array2[begin];
        array2[begin] = array2[i];
        array2[i] = temp;
        QuickSort(array1,array2,maxlen,begin,i);
        QuickSort(array1,array2,maxlen,j,end);
    }

}

void Dijkstra(GraphList *G, Path *P){
    InitPath(G,P);
    while(CanMove(G,P)){
        int min = FindMinPath(G,P);
        UpdatePath(G,P,min);
    }
}

void Output(GraphList *G, Path *P){
    int Path[MAX] = {0};
    int PathWeight[MAX] = {0};
    for(int i=1;i<G->vexNum;i++){
        if(P->visited[i]==-1){
            PathWeight[i] = -1;
        }
        else{
            PathWeight[i] = P->pathweight[G->vexs[i].vertex-1];
        }
        Path[i] = i+1;
    }
    QuickSort(PathWeight,Path,G->vexNum,1,G->vexNum-1);
    for(int i=1;i<G->vexNum;i++){
        if(PathWeight[i]>0){
            printf ("1 %d %d\n",Path[i],PathWeight[i]);
        }
    }
    for(int i=0;i<G->vexNum;i++){
        if (PathWeight[i]==-1){
            printf ("1 %d %d\n",Path[i],PathWeight[i]);
        }
    }
}

int main(){
    int m,n;
    scanf("%d %d",&n,&m);
    GraphList *G;
    Path *P;
    G = (GraphList*)malloc(sizeof(GraphList));
    P = (Path*)malloc(sizeof(Path));
    CreatGraphList(G,n,m);
    Dijkstra(G,P);
    Output(G,P);
    return 0;
}