知识点二十五：启发式搜索算法——A*算法

前言

魔兽世界、仙剑奇侠传这类 MMRPG（Multiplayer Online Role-PlayingGame） 游戏中，有一个非常重要的功能，那就是人物角色的自动寻路。当人物处于游戏地图中的某个位置的时候，我们用鼠标点击另外一个相对较远的位置，人物就会自动地绕过障碍物走过去。这个功能是怎么实现的呢？

路径搜索问题

实际上，这是一个非常典型的路径搜索问题。人物的起点就是他当下所在的位置，终点就是鼠标点击的位置。我们需要在地图中，找一条从起点到终点的路径。这条路径要绕过地图中所有障碍物，并且走的路不能太绕。

理论上讲，最短路径显然是最聪明的走法，是这个问题的最优解。不过，在之前最优出行路线规划的问题中，我们也讲过，如果为了计算两点之间的最短路径，在一个超级大图上动用 Dijkstra 算法，遍历所有的顶点和边，显然会非常耗时。在真实的软件开发中，我们所面对的是超级大的地图和海量的寻路请求，如果算法的执行效率太低，这显然是无法接受的。

其实，像出行路线规划、游戏寻路等这些真实软件开发中的问题，一般情况下，我们都不需要非得求出最优解（也就是最短路径）。在权衡路线规划质量和执行效率的情况下，我们只需要寻求一个次优解就足够了。那么，如何快速找出一条接近于最短路线的次优路线呢？这就要用到 A* 算法了。

启发式搜索算法

在介绍A* 算法之前，先介绍一下启发式搜索算法。不过在说它之前，我们还要先了解一下状态空间搜索。

状态空间搜索，就是将一个问题的求解过程表现为从初始状态到目标状态寻找一条路径的过程。通俗点说，就是要在两点之间求一条线路，这两点是问题的开始和问题的结果，而这一线路不一定是直线，可以是曲折的。由于求解问题的过程中分支有很多（即求解方式有很多种），到达目标状态的方式也就有很多，这主要是由于求解过程中求解条件的不确定性和不完备性造成的。求解的路径很多，这就构成了一个图，我们说这个图就是状态空间。问题的求解实际上就是在这个图中找到一条路径可以从问题的开始到问题的结果。这个寻找的过程就是状态空间搜索。

常用的状态空间搜索有广度优先搜索和深度优先搜索，但是它们存在着一个很大的缺陷，就是它们都是在一个给定的状态空间中穷举，都是根据搜索的顺序依次进行搜索，称为盲目搜索，在状态空间不大的时候可以用，但是如果状态空间非常大并且不可预测的情况下就不可取了，它们的效率会非常低。这时就需要用到启发式搜索。

启发式搜索算法，就是在状态空间中先对每一条搜索分支进行评估，得到最好的分支，再从这个分支继续搜索从而到达目标，这样可以有效省略大量无谓的搜索路径，大大提高了搜索效率。在启发式搜索中，对分支的评估是非常重要的，启发式搜索算法定义了一个估价函数 f(x)，与问题相关的启发式信息都被计算为一定的 f(x) 值，引入到搜索过程中。f(x) = g(x) + h(x)，其中 f(x) 是节点 x的估价函数，g(x)是在状态空间中从初始节点到节点 x的实际代价，h(x)是从节点 x到目标节点的最佳路径的估计代价。g(x)是已知的，所以在这里主要是 h(x) 体现了搜索的启发信息，h(x)专业的叫法是启发函数。换句话说，g(x)代表了搜索的广度的优先趋势。但是当 h(x) >> g(x)时，可以忽略g(x)，从而提高效率。

A* 算法

A* 算法正是利用启发式搜索策略来选择最优的扩展节点，从而提升效率的。实际上，A* 算法就是在 Dijkstra 算法的基础上进行优化和改造。

回顾一下 Dijkstra 算法的实现思路，其实有点儿类似广度优先搜索（BFS）算法，它每次找到跟起点最近的顶点，然后往外扩展。这种往外扩展的思路，其实有些盲目。为什么这么说呢？举一个例子，下面这个图对应一个真实的地图，每个顶点在地图中的位置，我们用一个二维坐标（x，y）来表示，其中，x 表示横坐标，y 表示纵坐标。每条边表示一条路，边上的权值代表路径的长度。

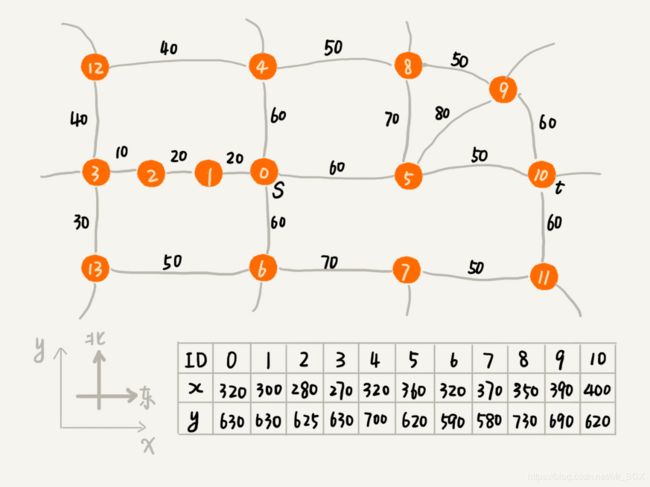
在 Dijkstra 算法的实现思路中，我们用一个优先级队列，来记录已经遍历到的顶点以及这个顶点与起点之间的路径长度。顶点与起点间的路径长度越小，越先被从优先级队列中取出来扩展，从图中举的例子可以看出，尽管我们期望找的是从起点 s 到终点 t 的路线，但是最先被搜索到的顶点依次是 1，2，3。这个搜索方向跟我们期望的路线方向是反着的，路线搜索的方向明显“跑偏”了。之所以会“跑偏”，那是因为我们是按照顶点与起点的路径长度的大小，来安排出队列顺序的。与起点越近的顶点，就会越早出队列。我们并没有考虑到这个顶点到终点的距离，所以，在地图中，尽管 1，2，3 三个顶点离起始顶点最近，但离终点却越来越远。

如果我们综合更多的因素，把这个顶点到终点可能还要走多远，也考虑进去，综合来判断哪个顶点该先出队列，那是不是就可以避免“跑偏”呢？

当我们遍历到某个顶点的时候，从起点走到这个顶点的路径长度是确定的，我们记作 g(i)（i 表示顶点编号）。但是，从这个顶点到终点的路径长度是未知的。虽然确切的值无法提前知道，但是我们可以用其他估计值来代替。这里我们可以通过这个顶点跟终点之间的直线距离，也就是欧几里得距离，来近似地估计这个顶点跟终点之间的路径长度（注意：路径长度跟直线距离是两个概念）。我们把这个距离记作 h(i)（i 表示这个顶点的编号），h(i) 专业的叫法是启发函数（heuristic function）。
由于欧几里得距离的计算公式，会涉及比较耗时的开根号计算，所以，我们一般通过另外一个更加简单的距离计算公式，那就是曼哈顿距离（Manhattan distance）。曼哈顿距离是两点之间横纵坐标的距离之和。计算的过程只涉及加减法、符号位反转，所以比欧几里得距离更加高效。

int hManhattan(Vertex v1, Vertex v2) { // Vertex表示顶点
  return Math.abs(v1.x - v2.x) + Math.abs(v1.y - v2.y);
}

原来在 Dijkstra 算法中，只是单纯地通过顶点 i 与起点之间的路径长度 g(i)，来判断谁先出队列，现在有了这个顶点到终点的路径长度估计值，我们可以通过两者之和 f(i)=g(i)+h(i)，来判断哪个顶点该最先出队列。综合两部分，我们就能有效避免刚刚讲的“跑偏”。这里 f(i) 的专业叫法是估价函数（evaluation function）。

从刚刚的描述，我们可以发现，A 算法实际上就只是对 Dijkstra 算法的简单改造*。实际上，代码实现方面，我们也只需要稍微改动几行代码，就能把 Dijkstra 算法的代码实现，改成 A* 算法的代码实现。将整个地图抽象成一个有向有权图的代码实现如下：

public class Graph { // 有向有权图的邻接表存储方法
  private LinkedList<Edge> adj[]; // 邻接表
  private int v; // 顶点个数

  public Graph(int v) {
    this.v = v;
    this.adj = new LinkedList[v];
    for (int i = 0; i < v; ++i) {
      this.adj[i] = new LinkedList<>();
    }
  }

  public void addEdge(int s, int t, int w) { // 添加一条边
    this.adj[s].add(new Edge(s, t, w));
  }

  private class Edge {
    public int sid; // 边的起始顶点编号
    public int tid; // 边的终止顶点编号
    public int w; // 权重
    public Edge(int sid, int tid, int w) {
      this.sid = sid;
      this.tid = tid;
      this.w = w;
    }
  }
  
  // 下面这个类是为了A* 算法实现中，顶点的定义
  private class Vertex { //顶点的定义
  	public int id; // 顶点编号ID
  	public int dist; // 从起始顶点到这个顶点的距离，也就是g(i)
  	public int f; // 估价函数 f(i)=g(i)+h(i)
  	public int x, y; // 顶点在地图中的坐标（x, y）
  	public Vertex(int id, int x, int y) {
    	this.id = id;
   		this.x = x;
    	this.y = y;
    	this.f = Integer.MAX_VALUE;
    	this.dist = Integer.MAX_VALUE;
  	}
  }
  
  // Graph类的成员变量，在构造函数中初始化
  Vertex[] vertexes = new Vertex[this.v];
  // 新增一个方法，添加顶点的横纵坐标
  public void addVetex(int id, int x, int y) {
  	vertexes[id] = new Vertex(id, x, y)
  }
}

在 A* 算法的代码实现中，图 Graph 类的定义跟 Dijkstra 算法中的定义一样。而顶点 Vertex 类的定义，跟 Dijkstra 算法中的定义，稍微有点儿区别，多了 x，y 坐标，以及刚刚提到的 f(i) 值。而 A* 算法代码实现的主要逻辑是下面这段代码。它跟 Dijkstra 算法的代码实现，主要有 3 点区别：

• 优先级队列构建的方式不同。A* 算法是根据 f(i) 值（f(i)=g(i)+h(i)）来构建优先级队列，而 Dijkstra算法是根据 dist 值（也就是刚刚讲到的 g(i)）来构建优先级队列；
• A* 算法在更新顶点 dist 值的时候，会同步更新 f(i) 值；
• 循环结束的条件也不一样。Dijkstra 算法是在终点出队列的时候才结束，A* 算法是一旦遍历到终点就结束。

private class PriorityQueue { // 根据vertex的f值构建小顶堆，而不是按照dist
  private Vertex[] nodes;
  private int count;
  public PriorityQueue(int v) {
    this.nodes = new Vertex[v+1];
    this.count = v;
  }
  public Vertex poll() 
  public void add(Vertex vertex) 
  // 更新结点的值，并且从下往上堆化，重新符合堆的定义。时间复杂度O(logn)。
  public void update(Vertex vertex) 
  public boolean isEmpty() 
}

public void astar(int s, int t) { // 从顶点s到顶点t的路径
  int[] predecessor = new int[this.v]; // predecessor 数组记录每个顶点的前驱顶点，用来还原最短路径
  PriorityQueue queue = new PriorityQueue(this.v); // 根据vertex的f值构建小顶堆
  boolean[] inqueue = new boolean[this.v]; // 标记是否进入过队列
  vertexes[s].dist = 0; // 把起始顶点 s 的 dist 值初始化为 0
  vertexes[s].f = 0; // 把起始顶点 s 的 f 值初始化为 0
  queue.add(vertexes[s]); // 将起始顶点 s 添加到优先级队列中
  inqueue[s] = true;
  while (!queue.isEmpty()) {
    Vertex minVertex = queue.poll(); // 取堆顶元素并删除
    for (int i = 0; i < adj[minVertex.id].size(); ++i) {
      Edge e = adj[minVertex.id].get(i); // 取出一条与minVetex相连的边 e
      Vertex nextVertex = vertexes[e.tid]; // 边 e指向的顶点为nextVertex，即取出的有向边为：minVertex-->nextVertex
      if (minVertex.dist + e.w < nextVertex.dist) { // 若存在更短的路径，更新nextVertex的dist,f
        nextVertex.dist = minVertex.dist + e.w; // 更新顶点 dist值
        nextVertex.f = nextVertex.dist + hManhattan(nextVertex, vertexes[t]); // 同步更新 f值
        predecessor[nextVertex.id] = minVertex.id;
        if (inqueue[nextVertex.id] == true) { // 如果这个顶点已经在优先级队列中了，就不要再将它重复添加进去，直接更新队列中该顶点的dist值即可
          queue.update(nextVertex);
        } else {
          queue.add(nextVertex);
          inqueue[nextVertex.id] = true; // 每当有新的顶点进入队列后，要在 inqueue数组中标记
        }
      }
      if (nextVertex.id == t) { // 一旦遍历到终点 t就可以结束while了
        queue.clear(); // 只有清空queue，才能推出while循环
        break; // 这里的break 只能退出for循环
      }
    }
  }
  // 输出路径
  System.out.print(s);
  print(s, t, predecessor); 
}

private void print(int s, int t, int[] predecessor) { // 通过递归的方式，将路径打印出来
  if (s == t) return;
  print(s, predecessor[t], predecessor);
  System.out.print("->" + t);
}

尽管 A* 算法可以更加快速的找到从起点到终点的路线，但是它并不能像 Dijkstra 算法那样，找到最短路线。这是为什么呢？

要找出起点 s 到终点 t 的最短路径，最简单的方法是，通过回溯穷举所有从 s 到达 t 的不同路径，然后对比找出最短的那个。不过很显然，回溯算法的执行效率非常低，是指数级的。

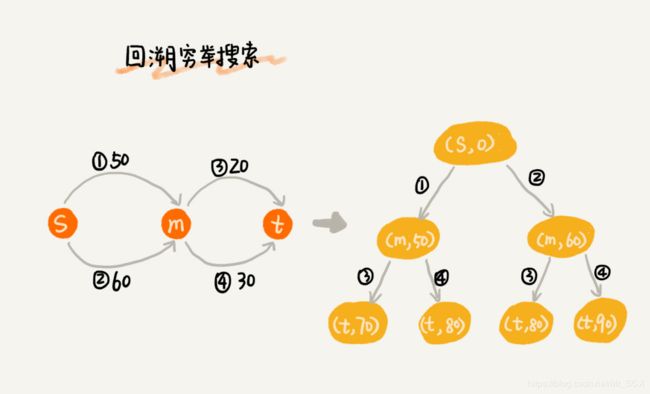
Dijkstra 算法在此基础之上，利用动态规划的思想，对回溯搜索进行了剪枝，只保留起点到某个顶点的最短路径，继续往外扩展搜索。动态规划相较于回溯的穷举搜索，只是换了一个实现思路，但它实际上也考察到了所有从起点到终点的路线，所以才能得到最优解。

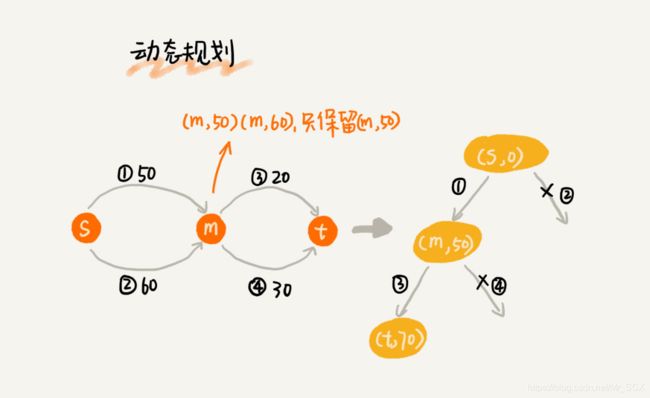
而 A* 算法之所以不能像 Dijkstra 算法那样，找到最短路径，主要原因是两者的 while 循环结束条件不一样。刚刚我们讲过，Dijkstra 算法是在终点出队列的时候才结束循环，A* 算法是一旦遍历到终点就结束循环。对于 Dijkstra 算法来说，当终点出队列的时候，终点的 dist 值是优先级队列中所有顶点的最小值，即便再运行下去，终点的 dist 值也不会再被更新了。对于 A* 算法来说，一旦遍历到终点，我们就结束 while 循环，这个时候，终点的 dist 值未必是所有顶点中的最小值。换句话说，A* 算法是利用贪心算法的思路，每次都找 f 值最小的顶点出队列，一旦搜索到终点就清空优先队列，退出while循环，不再继续考察其他顶点和路线了。所以，它并没有考察所有的路线，也就不可能找出最短路径了。

解答开篇：如何用A*搜索算法实现游戏中的寻路功能？

要利用 A* 算法解决这个问题，我们只需要把地图抽象成图就可以了。不过，游戏中的地图跟我们平常用的地图软件中的地图是不一样的。因为游戏中的地图并不像我们现实生活中那样，存在规划非常清晰的道路，更多的是宽阔的荒野、草坪等。所以，我们也就没法利用之前讲到的抽象方法，把地图上的岔路口抽象成顶点，把岔路口与岔路口之间的路抽象成边。

实际上，我们可以换一种抽象的思路，把整个地图分割成一个一个的小方块。在某一个方块上的人物，只能往上下左右四个方向的方块移动。我们可以把每个方块抽象成一个顶点，在两个相邻的方块之间连接两条有向边，并且边的权值都是 1。所以，这个问题就转化成，在一个有向有权图中，找某个顶点到另一个顶点的路径问题。将游戏地图抽象成边权值为 1 的有向图之后，我们就可以套用 A* 算法，来实现游戏中人物的自动寻路功能了。

小结

一、启发式搜索算法
1.常用的状态空间搜索有广度优先和深度优先搜索算法，但是它们存在着一个很大的缺陷，就是都是在一个给定的状态空间中穷举，都是根据搜索的顺序依次进行搜索，称为盲目搜索，在状态空间不大的时候可以用，但是如果状态空间非常大并且不可预测的情况下就不可取了，它们的效率会非常低。
2. 而启发式搜索算法就是在状态空间中先对每一条搜索分支进行评估，得到最好的分支，再从这个分支继续搜索从而到达目标。在启发式搜索中，利用当前与问题有关的信息作为启发式信息指导搜索，这些信息能够有效省略大量无谓的搜索路径，大大提高了搜索效率。
3. 在启发式搜索中，对分支的评估是非常重要的，如何利用这些启发式信息，启发式搜索算法定义了一个估价函数 f(x)，与问题相关的启发式信息都被计算为一定的 f(x) 的值，引入到搜索过程中。f(x) = g(x) + h(x)，其中 f(x) 是节点 x的估价函数，g(x)是在状态空间中从初始节点到节点 x的实际代价，h(x)是从节点 x到目标节点的最佳路径的估计代价。g(x)是已知的，所以在这里主要是 h(x) 体现了搜索的启发信息，h(x)专业的叫法是启发函数。换句话说，g(x)代表了搜索的广度的优先趋势。但是当 h(x) >> g(x)时，可以忽略g(x)，从而提高效率。
4. 启发式搜索算法利用估价函数，避免“跑偏”，贪心地朝着最有可能到达终点的方向前进。这种算法找出的路线，并不是最短路线。不过，鉴于启发式搜索算法能很好地平衡路线质量和执行效率，它在实际的软件开发中的应用更加广泛。
5. 算法实例：A* 算法、IDA* 算法、蚁群算法、遗传算法、模拟退火算法等。

二、A* 算法
1.A* 算法就是对 Dijkstra 算法的简单改造。它跟 Dijkstra 算法的代码实现，主要有 3 点区别：
（1）优先级队列构建的方式不同。A* 算法是根据估价函数 f(i) 的值（f(i)=g(i)+h(i)，其中g(i)表示顶点 i 与起点间的路径长度，h(i)表示顶点 i 到终点的路径长度估计值）来构建优先级队列，而 Dijkstra 算法是根据顶点与起点间的路径长度 dist 值（也就是 g(i)）来构建优先级队列的；
（2）A* 算法每次在更新顶点 i 的 dist 值的时候，也会同步更新 f(i) 值；
（3）循环结束的条件也不一样。Dijkstra 算法是在终点出队列的时候才结束，A* 算法是一旦遍历到终点就结束。
2. 尽管 A* 算法可以更加快速的找到从起点到终点的路线，但是它并不能像 Dijkstra 算法那样，找到最短路线。A* 算法实际上是利用贪心算法的思路，每次都找 f 值最小的顶点出队列，一旦搜索到终点就不再继续考察其他顶点和路线了。所以，它并没有考察所有的路线，也就不可能找出最短路径了。
3. A* 算法应用场景：地图 App 中的出行路线规划问题、游戏中人物角色的自动寻路功能。

参考

《数据结构与算法之美》
王争
前Google工程师