【面试题】股票买卖系列问题（一个 dp框架打尽 6道题目）

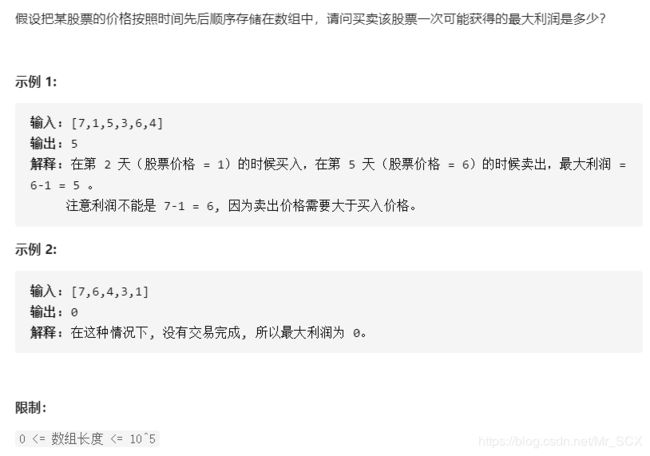
题目一

解法一

base case处理
因为i从 0开始，i= -1表示还没开始，利润当然为0，故dp[-1][0]=0；
而还没开始不可能持有股票，故dp[-1][1] 定义为负无穷
dp[0][0]
= max(dp[-1][0], dp[-1][1] + prices[i])  
= max(0, -infinity + prices[i]) 
= 0
dp[0][1]
= max(dp[-1][1], dp[-1][0] - prices[i])  
= max(-infinity， 0 - prices[i]) 
= -prices[i]

class Solution {
    public int maxProfit(int[] prices) {
        if(prices.length == 0) return 0;
        int[][] dp = new int[prices.length][2]; // 只能交易一次，dp[i][j]表示的是第 i天有没有持有股票(j只有两种状态，0 表示不持有或 1表示持有)
        dp[0][0] = 0;
        dp[0][1] = -prices[0];
        for(int i=1; i<prices.length; i++) {
            dp[i][0] = Math.max(dp[i-1][0], dp[i-1][1] + prices[i]);
            dp[i][1] = Math.max(dp[i-1][1], -prices[i]);
        }
        return dp[prices.length-1][0]; // 最后需要的结果是到了最后一天，手上没有持有股票
    }
}

新状态只和相邻的一个状态有关，其实不需要用到整个 dp 数组，只需要一个变量储存相邻的之前那个状态就足够了，这样可以把空间复杂度降到 O(1)

class Solution {
    public int maxProfit(int[] prices) {
        if(prices.length == 0) return 0;
        // base case：dp[-1][0] = 0, dp[-1][1] = -infinity
        int dp_i_0 = 0, dp_i_1 = Integer.MIN_VALUE;
        for(int i=0; i<prices.length; i++) {
            // 今天不持有股票对应了两种可能：（1）昨天也同样不持有股票，今天继续保持（2）昨天本持有股票，今天卖出了，那就要加上今天这笔交易所获利润
            dp_i_0 = Math.max(dp_i_0, dp_i_1+prices[i]); 
            // 今天持有股票对应了两种可能：（1）昨天已经持有股票，今天继续保持（不卖出）（2）昨天本不持有股票，今天买入了，那就要加上今天这笔交易所花成本
            dp_i_1 = Math.max(dp_i_1, -prices[i]);
        }
        return dp_i_0; // 因为只能交易一次，最后一天肯定是不持有股票比持有的利润高
    }
}

题目二

解法一

此题目变成不限制交易次数了，也就不需要记录交易次数这个状态了。

class Solution {
    public int maxProfit(int[] prices) {
        if(prices.length == 0) return 0;
        int[][] dp = new int[prices.length][2];
        // base case     
        dp[0][0] = 0; 
        dp[0][1] = -prices[0];
        for(int i=1; i<prices.length; i++) {
    		// 今天不持有股票对应了两种可能：（1）昨天也同样不持有股票，今天继续保持（2）昨天本持有股票，今天卖出了，那就要加上今天这笔交易所获利润
            dp[i][0] = Math.max(dp[i-1][0], dp[i-1][1]+prices[i]);
    		// 今天持有股票对应了两种可能：（1）昨天已经持有股票，今天继续保持（不卖出）（2）昨天本不持有股票，今天买入了，那就要加上今天这笔交易所花成本
            dp[i][1] = Math.max(dp[i-1][1], dp[i-1][0]-prices[i]);
        }
        return dp[prices.length-1][0];
    }
}

同样地，这个题目也不需要用到整个 dp 数组，只需要两个变量储存昨天和今天的两个状态就足够了，这样可以把空间复杂度降到 O(1)。

class Solution {
    public int maxProfit(int[] prices) {
        if(prices.length == 0) return 0;
        int dp_i_0 = 0, dp_i_1 = Integer.MIN_VALUE;
        for(int i=0; i<prices.length; i++) {
            int tmp = dp_i_0; // 由于dp_i_0下面一行可能会改变，先备份其原先的值
            dp_i_0 = Math.max(dp_i_0, dp_i_1+prices[i]);
            dp_i_1 = Math.max(dp_i_1, tmp-prices[i]);
        }
        return dp_i_0;
    }
}

题目三

解法一

这题和上一题很类似，同样不限制交易次数，只不过这里有一个冷冻期的要求，每次 sell 之后要等一天才能继续交易。解决方案，只要把这个特点融入上一题的状态转移方程即可。

dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
dp[i][1] = max(dp[i-1][1], dp[i-2][0] - prices[i])
解释：第 i 天选择 buy 的时候，要从 i-2 的状态转移，而不是 i-1（因为第 i-1天卖出时是没有办法马上在下一天即第 i天买入的）。

=============base case处理====================
因为i从 0开始，i= -1表示还没开始，利润当然为0，故dp[-1][0]=0；而还没开始时，是不可能持有股票的，故dp[-1][1] 定义为负无穷-infinity
dp[0][0]
= max(dp[-1][0], dp[-1][1] + prices[0])  
= max(0, -infinity + prices[0])
= 0
由于这道题引入了一个冷冻期的限制，故第 0天选择买入时，状态要从第 0-2天不持有的状态转移过来（因为若是第 i-1天刚卖出是无法在第 i天就买入的）。而 i=-2时显然也还没开始，故dp[-2][0]=0
dp[0][1]
= max(dp[-1][1], dp[-2][0] - prices[0])
= max(-infinity， 0 - prices[0])
= -prices[0]

class Solution {
    public int maxProfit(int[] prices) {
        if(prices.length <= 1) return 0; // 小于2天不可能完成交易，利润一定为0
        int[][] dp = new int[prices.length][2];
        // base case
        dp[0][0] = 0;
        dp[0][1] = -prices[0];
        dp[1][0] = Math.max(dp[0][0], dp[0][1]+prices[1]);
        dp[1][1] = Math.max(dp[0][1], -prices[1]); // dp[1][1] = max(dp[0][1], dp[-1][0] - prices[1]) = max(-prices[0], -prices[1]);
        for(int i=2; i<prices.length; i++) { // i从2开始
            dp[i][0] = Math.max(dp[i-1][0], dp[i-1][1]+prices[i]);
            dp[i][1] = Math.max(dp[i-1][1], dp[i-2][0]-prices[i]); 
        }
        return dp[prices.length-1][0];
    }
}

同样地，这道题也可以优化空间效率。

class Solution {
    public int maxProfit(int[] prices) {
        if(prices.length <= 1) return 0;
        int dp_i_0 = 0, dp_i_1 = Integer.MIN_VALUE;
        int dp_pre_0 = 0; // 代表 dp[i-2][0]
        for(int i=0; i<prices.length; i++) {
            int tmp = dp_i_0; // 先记录 dp[i-1][0]
            dp_i_0 = Math.max(dp_i_0, dp_i_1+prices[i]); // dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
            dp_i_1 = Math.max(dp_i_1, dp_pre_0-prices[i]); // dp[i][1] = max(dp[i-1][1], dp[i-2][0] - prices[i])
            dp_pre_0 = tmp; // 此轮的 dp[i-1][0]即为下一轮的 dp[i-2][0]
        }
        return dp_i_0;
    }
}

题目四

这道题同样是不限制交易次数，只不过现在要求每次交易要支付手续费，只要把手续费从利润中减去即可。状态转移方程改写为：

dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
dp[i][1] = max(dp[i-1][1], dp[i-1][0] - prices[i] - fee)
解释：相当于买入股票的价格升高了。
在第一个式子里减也可以，相当于卖出股票的价格减小了。

每一步交易需要扣除手续费，可以选择在买入时减去，或选择在卖出时减去。

class Solution {
    public int maxProfit(int[] prices, int fee) {
        if(prices.length <= 1) return 0;
        int dp_i_0 = 0, dp_i_1 = Integer.MIN_VALUE;
        for(int i=0; i<prices.length; i++) {
            int tmp = dp_i_0; // 先记录 dp[i-1][0]
            dp_i_0 = Math.max(dp_i_0, dp_i_1+prices[i]);
            dp_i_1 = Math.max(dp_i_1, dp_i_0-prices[i]-fee); 
        }
        return dp_i_0;
    }
}

题目五

解法一

k = 2 和前面题目的情况稍微不同，因为上面几道题目的情况都和 k 的关系不太大。要么 k 是正无穷，即在状态转移过程中 k 和 k-1是一样的，即 k 对状态转移已经没有影响了，就不需要穷举 k的情况；要么 k = 1，跟 k = 0 这个 base case 挨得近，之后在状态转移的过程中 k=1 始终不会改变，即 k 对状态转移已经没有影响了，故也不需要穷举 k的情况。

但是，当 k=2 或者 k=任意正整数时，就需要考虑每天剩余交易次数 k的大小对股票买卖的影响了。这样一来，原始的动态转移方程，就没有可化简的地方了。

/**
* dp[i][k][0]: 第 i天，最多还可以交易 k次，现在手上不持有股票
* dp[i][k][1]: 第 i天，最多还可以交易 k次，现在手上持有股票
* 由于买入卖出才算一次完整的交易，因为 k-1选择在买入时或卖出时中一个状态执行即可
*/
dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i])
/** 解释
* 今天没有持有股票，有两种可能：
* (1) 要么是昨天就没有持有，然后今天选择保持，所以今天还是没有持有股票；
* (2) 要么是昨天持有股票，但是今天卖出（利润+股票价格）了，所以今天没有持有股票了。
*/
dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i])
/** 解释
* 今天持有股票，有两种可能：
* (1) 要么是昨天就已经持有着股票，然后今天选择保持，所以今天还持有着股票；
* (2) 要么是昨天本没持有股票，但是今天买入（利润-股票价格）了，所以今天就持有股票了。
*/

这道题由于没有消掉 k 的影响，所以在状态转移过程中必须要对 k 进行穷举：

class Solution {
    public int maxProfit(int[] prices) {
        if(prices.length <=1) return 0;
        int max_k = 2;
        int n = prices.length;
        int[][][] dp = new int[n][max_k+1][2];
        for(int i=0; i<n; i++){
            for(int k=max_k; k>0; k--){
                if(i == 0) { // 单独处理一下 base case
                    dp[i][k][0] = 0;
                    dp[i][k][1] = -prices[i];
                    continue;
                }
                dp[i][k][0] = Math.max(dp[i-1][k][0], dp[i-1][k][1] + prices[i]);
                dp[i][k][1] = Math.max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i]);
            }
        }
        return dp[n-1][max_k][0]; // 最后想要的答案是：最后一天，最多允许 max_k 次交易，最多获得多少利润
    }
}

题目六

一次交易由买入和卖出构成，至少需要两天。所以说有效的限制 k 应该不超过总天数的一半 n/2，如果超过了，那在 n天内交易次数 k一定不会用完的，即 k 没有约束作用了，相当于 k = +infinity 的情况，可以直接复用之前题目二的代码。

class Solution {
    public int maxProfit(int k, int[] prices) {
        int n = prices.length;
        if(n <= 1) return 0;
        // 若 k超过了 n/2，限制交易次数无论如何在 n天内都不会用完，此时 k对股票买卖已经没有约束作用了，相当于 k是正无穷的情况
        if(k > n/2) return maxProfit_k_inf(prices);
        int[][][] dp = new int[n][k+1][2];
        for(int i=0; i<n; i++) { // 枚举每一天的情况
            for(int j=k; j>0; j--) { // 枚举剩余交易次数的情况
                if(i == 0) { // 单独处理 base case
                    dp[i][j][0] = 0;
                    dp[i][j][1] = -prices[i];
                }else {
                    dp[i][j][0] = Math.max(dp[i-1][j][0], dp[i-1][j][1]+prices[i]);
                    dp[i][j][1] = Math.max(dp[i-1][j][1], dp[i-1][j-1][0]-prices[i]);
                }
            }            
        }
        return dp[n-1][k][0];
    }

    public int maxProfit_k_inf(int[] prices) { // k为正无穷时的解法
        int n = prices.length;
        int dp_i_0 = 0, dp_i_1 = Integer.MIN_VALUE;
        for(int i=0; i<n; i++) {
            int tmp = dp_i_0;
            dp_i_0 = Math.max(dp_i_0, dp_i_1+prices[i]);
            dp_i_1 = Math.max(dp_i_1, tmp-prices[i]);
        }
        return dp_i_0;
    }
}

参考

团灭LeetCode股票买卖问题