AAAI 2020 SR+ITM论文:JSI-GAN
JSI-GAN: GAN-Based Joint Super-Resolution and Inverse Tone-Mapping with Pixel-Wise Task-Specific Filters for UHD HDR Video
- 摘要
- Introduction
- Proposed Method
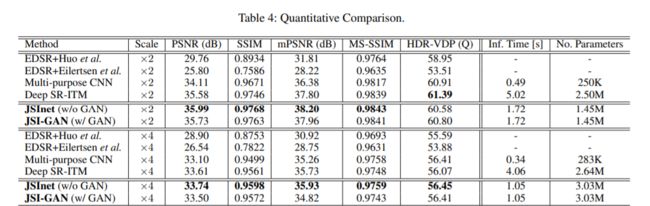
- 实验结果
摘要
使用分治策略来处理SR-iTM问题;将其分成三个任务相关的子网络:图像重建子网络(image reconstruction subnet),细节恢复子网络 (detail restoration subnet),局部对比度增强子网络(local contrast enhancement subnet),从而学习到一组像素级的逐像素的1维可分离卷积用于复原细节,像素级的2维局部卷积核来用于对比度增强。此外,作者提出一种可增强细节信息的GAN loss,可同时增强细节恢复和对比度复原。
代码链接: https://github.com/JihyongOh/JSI-GAN
Introduction
一方面,作者认为SR-ITM这个问题需要同时考虑两个问题:如何在上采样的结果中恢复细节;由于比特位数增加如何增强局部的对比度信息(enhance local contrast)
GAN网络可用于生成图片,但作者认为GAN网络会导致主观的图像质量提高的同时降低客观的评价指标(PSNR,SSIM),直接使用传统的GAN网络的结构会导致缺少相应的细节和局部的对比度,因此本文中使用了新的detail loss,使得生成的图片与GT的细节更相符合,并且使用一种feature-matching loss,用来减轻在训练过程中客观评价的drop。
Contributions:
1.提出JSI-GAN,使用新的detail loss和feature-matching loss用于保证细节的复原和训练的稳定性。
2.将网络的生成器设计为任务相关,在局部细节复原中使用逐像素的一维可分类的filter;在local contrast enhancement问题中使用2D局部filter。
3.DR(detail restoration)子网络精巧地恢复高分辨率的HDR输出结果,LCE(local contrast enhancement)子网络有效地恢复局部的曝光度。
Proposed Method
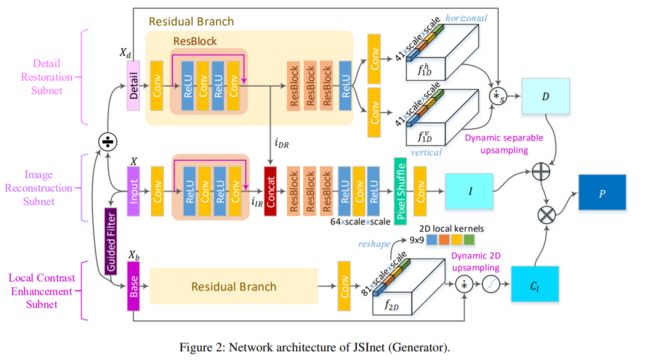
下图为生成器JSINet,分成细节恢复子网络,图像重建子网络和局部对比度增强子网络。
细节恢复子网络(detail restoration subnet): X d = X ⊘ X b X_d = X \oslash X_b Xd=X⊘Xb, X b X_b Xb是X经过guided filter后的结果; ⊘ \oslash ⊘表示的是逐像素的乘积;为防止出现除0的情况,在分母 X b X_b Xb上加上了一个极小值 1 0 − 15 10^{-15} 10−15。 X d X_d Xd用于生成一维的水平和垂直的可分离filter。最后生成41 × \times ×scale × \times ×scale,41是一维可分离卷积核的长度,scale × \times ×scale代表着超分问题的上采样scale。从而获得动态可分离上采样操作: D = X d ∗ ˙ s ( f 1 D v , f 1 D h ) D = X_d {\dot\ast_s}(f_{1D}^v,f_{1D}^h) D=Xd∗˙s(f1Dv,f1Dh)
生成的filter是与位置相关的,也是与细节相关的,不同的卷积核用于生成不同细节的特征,而不是使用固定的卷积核用于训练。(dynamic filter for sr)k=41的一维可分离卷积核与9x9的filter的参数几乎是一样的。
局部对比度增强网络:经过guided filter的 X b X_b Xb用于增强局部的对比度。LCE子网络在每个像素区域生成一个9x9的二维的local filter。最后生成的LCE结果 C l = 2 × s i g m o i d ( X b ∗ ˙ f 2 D ) C_l=2\times sigmoid(X_b\dot\ast f_{2D}) Cl=2×sigmoid(Xb∗˙f2D)
图像重建子网络:如下图所示,最后生成的结果 P = ( I + D ) × C l P= (I+D)\times C_l P=(I+D)×Cl
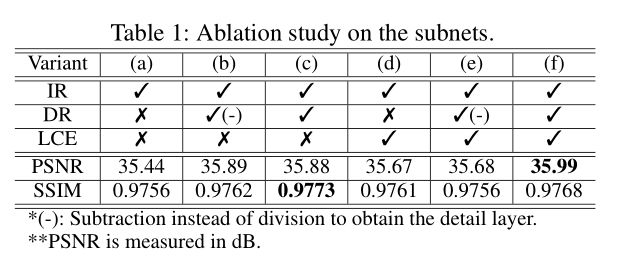
Ablation Study 如下图所示:
Discriminator的设计如下,使用了spectral normalization(借鉴了SN-GAN)用来使GAN训练更加稳定。输出如下:
D f ( x ) = ( B N ∘ F C 1 ∘ B N ∘ F C 512 ∘ L R L ∘ B N ∘ 4 C o n v 2 ∘ D B 4 ∘ L R L ∘ 3 C o n v 1 ) ( x ) D^f(x)=(BN\circ FC1\circ BN \circ FC512 \circ LRL \circ BN \circ 4Conv2\circ DB^4 \circ LRL \circ 3Conv1)(x) Df(x)=(BN∘FC1∘BN∘FC512∘LRL∘BN∘4Conv2∘DB4∘LRL∘3Conv1)(x)
其中LRL是参数为0.2的LeaKy ReLU,FC k k k是有k层输出的全连接层, k C o n v s kConvs kConvs代表着k × \times ×k的卷积核。 D B n DB^n DBn代表着n次DisBlocks层,
使用了RaHinge GAN
L a d v D = E Y [ m a x ( 0 , Q ~ Y , P ( − ) ) ] + E P [ m a x ( 0 , Q ~ P , Y ( + ) ) ] L_{adv}^D=\mathbb{E}_Y[max(0,\tilde{Q}_{Y,P}^{(-)})]+\mathbb{E}_P[max(0,\tilde{Q}_{P,Y}^{(+)})] LadvD=EY[max(0,Q~Y,P(−))]+EP[max(0,Q~P,Y(+))]
L a d v G = E P [ m a x ( 0 , Q ~ P , Y ( − ) ) ] + E Y [ m a x ( 0 , Q ~ Y , P ( + ) ) ] L_{adv}^G=\mathbb{E}_P[max(0,\tilde{Q}_{P,Y}^{(-)})]+\mathbb{E}_Y[max(0,\tilde{Q}_{Y,P}^{(+)})] LadvG=EP[max(0,Q~P,Y(−))]+EY[max(0,Q~Y,P(+))]
其中, Q ~ P , Y ( ± ) = 1 ± D ~ P , Y , D ~ P , Y = D f ( P ) − E Y D f ( Y ) \tilde{Q}_{P,Y}^{(\pm)}=1\pm \tilde{D}_{P,Y},\tilde{D}_{P,Y}=D_f(P)-\mathbb{E}_YD_f(Y) Q~P,Y(±)=1±D~P,Y,D~P,Y=Df(P)−EYDf(Y),P是生成的图像,Y是GT图像。
同样本文提出了feature-matching loss L f m = ∑ i = 1 4 ∣ ∣ f m i ( Y ) − f m i ( P ) ∣ ∣ 2 L_{fm}=\sum_{i=1}^4 ||f_{m_i}(Y)-f_{m_i}(P)||_2 Lfm=∑i=14∣∣fmi(Y)−fmi(P)∣∣2
最终的损失函数为 L G = λ r e c ⋅ ∣ ∣ Y − P ∣ ∣ 2 + λ a d v ⋅ ( L a d v G + λ d ⋅ L a d v d , G ) + λ f m ⋅ ( L f m + λ d ⋅ L f m d ) L_G=\lambda_{rec}\cdot ||Y-P||_2 +\lambda_{adv}\cdot(L_{adv}^G+\lambda_d\cdot L_{adv}^{d,G} )+\lambda_{fm}\cdot(L_{fm}+\lambda_d\cdot L_{fm}^d) LG=λrec⋅∣∣Y−P∣∣2+λadv⋅(LadvG+λd⋅Ladvd,G)+λfm⋅(Lfm+λd⋅Lfmd)
Detail GAN Loss
懒得写了,这个loss可以使得网络训练的更稳定。