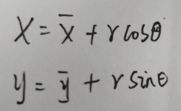Opencv 基础知识点整理——几何变换
几何变换
分两个步骤:空间坐标变换→插值算法
空间坐标变换包括三类:仿射变换、投影变换、极坐标变换
仿射变换:仿射变换的功能就是实现图片的平移、缩放、旋转。
实现此功能的核心是拥有一个仿射变换矩阵,如下所示:
其中矩阵A即为仿射变换矩阵,此矩阵需自己提供。
进行仿射变换之后就需要用到插值算法才能将其运用到几何变换的图像中去。主要原因是插值后的坐标点有可能不是整数,插值是将小数变为整数。
插值算法: 最邻近插值、双线性插值、三次样条插值等
最邻近插值:就是从(x,y)的四个相邻整数中选择最近的作为插值后的值,这种方法插值会出现锯齿状外观,对图像放大处理的效果会更明显。
双线性插值:双线性插值就是利用周围四个整数点先通过水平方向进行插值,后通过垂直方向进行插值,得到最终结果。
三次样条插值:略。
投影变换:与仿射变换类似,但属于三维空间中的旋转变换。
此方法与仿射变换类似,但需要提供图片的变换前的四个点坐标和对应的变换后的四个点坐标。
Eg. 原坐标为[[0,0],[200.0],[0,200].[200,200]],
对应的投影变换后的坐标为:[[100,20],[200,20],[50,70],[250,70]]
则投影变换矩阵为[[5.0000e-01,-3.75000e-01,1.0000e+02],
[3.88578059e-16,5.000e-02,2.000000e+01],
[9.54097912e-18,-2.50e-03,1.0000e+00]]
即通过变换前后的四个对应点的坐标来进行投影变换。
极坐标变换:利用极坐标变换来校正图像中的圆形物体或被包含在圆环中的物体。
笛卡尔坐标转极坐标公式如下:
以变换中心为圆心的同一个圆上的点,在极坐标系θor中显示为一条直线。
极坐标转笛卡尔坐标:
返回的是以(0,0)为中心的笛卡尔坐标,即返回的是(x-x1,y-y1),此处x1,y1代表以(x1,y1)为原点的坐标系。