信号与系统(Python) 学习笔记摘录 (3) LTI 系统 与 滤波器

• 【总目录】
  • (1) 简介 Intro
  • (2) 傅里叶 Fourier
    • 常用函数的傅里叶变换汇总
  • (3) LTI 系统 与 滤波器
    • 二次抑制载波振幅调制接收系统 Python
  • (4) 取样 Sampling
  • (5) 离散傅里叶 Discrete Fourier

---

3. LTI 系统 与 滤波器

$$f(t)\to \boxed{\text{LTI (linear time-invariant systems)}}\to y(t)$$
$$f(t)\to \boxed{h(t)}\to y(t)$$
$$y(t)=f(t)\star h(t)$$

---

3.1. 频域分析

3.1.1. 基本信号

• 傅里叶分析是将任意信号分解为无穷多项不同频率的虚指数函数之和。

• 周期信号:
  $$f_T(t)=\sum _{n=-\infty }^{\infty }{F}_n{e}^{jn\Omega t}$$

  • 基本信号 $e^{jn\Omega t}$

• 非周期信号:
  $$f(t)=\frac{1}{2\pi }{\int }_{-\infty }^{\infty }F(j\omega )e^{j\omega t}d\omega$$

  • 基本信号 $e^{j\omega t}$

• 频域分析中，基本信号的定义域为 $(–\infty ，\infty )$ ，而 $t=–\infty$ 总可认为系统的状态为 $0$ ，因此傅里叶分析中的响应指零状态响应，常写为 $y(t)$。

• 设 LTI 系统的冲激响应为 $h(t)$ ，当激励是角频率 $\omega$ 的基本信号 $e^{j\omega t}$ 时，其响应
  $$y(t)=h(t)\star e^{j\omega t}$$

  • 根据卷积定义, 可得
    $$\begin{array}{rl}y(t)& ={\int }_{-\infty }^{\infty }h(\tau )e^{j\omega (t-\tau )}d\tau \\ & ={\int }_{-\infty }^{\infty }h(\tau )e^{-j\omega \tau }d\tau \cdot e^{j\omega t}\\ & =\mathfrak{F}[h(t)]\cdot e^{j\omega t}\\ & =H(j\omega )\cdot e^{j\omega t}\end{array}$$

• $h(t)$ 的傅里叶变换，记为 $H(j\omega )$ ，常称为系统的频率响应函数。
  $$H(j\omega )=\mathfrak{F}[h(t)]={\int }_{-\infty }^{\infty }h(\tau )e^{-j\omega \tau }d\tau$$

• $H(j\omega )$ 反映了响应 $y(t)$ 的幅度和相位

$$e^{j\omega t}\to \boxed{h(t)}\to H(j\omega )\cdot e^{j\omega t}$$

3.1.2. 傅里叶变换分析法

• 一般信号
  $$\begin{array}{rl}{e}^{j\omega t}& \to \boxed{h(t)}\to H(j\omega )\cdot e^{j\omega t}\downarrow \text{齐次性}\\ \frac{1}{2\pi }F(j\omega )d\omega \cdot e^{j\omega t}& \to \boxed{h(t)}\to \frac{1}{2\pi }F(j\omega )d\omega \cdot H(j\omega )e^{j\omega t}\downarrow \text{可加性}\\ \frac{1}{2\pi }{\int }_{-\infty }^{\infty }F(j\omega )e^{j\omega t}d\omega & \to \boxed{h(t)}\to \frac{1}{2\pi }{\int }_{-\infty }^{\infty }H(j\omega )F(j\omega )\cdot e^{j\omega t}d\omega \\ f(t)& \to \boxed{h(t)}\to y(t)={\mathfrak{F}}^{-1}[F(j\omega )H(j\omega )]\\ F(j\omega )& \to \boxed{H(j\omega )}\to Y(j\omega )=F(j\omega )\cdot H(j\omega )\\ f(t)& \to \boxed{h(t)}\to y(t)=f(t)\star h(t)\end{array}$$

• 步骤:

  1. 求输入信号 $f(t)$ 的傅里叶变换 $F(j\omega )$ ;
  2. 求系统函数 $H(j\omega )$ ;
  3. 求零状态响应 $y(t)$ 的傅里叶变换 $Y(j\omega )=F(j\omega )\cdot H(j\omega )$ ;
  4. 求 $Y(j\omega )$ 的傅里叶逆变换 $y(t)={\mathfrak{F}}^{-1}[F(j\omega )H(j\omega )]$ 。

3.1.3. 傅里叶级数分析法

• 对周期输入信号，还可用傅里叶级数分析法

• 周期信号的指数形式傅里叶级数:
  $$f_T(t)=\sum _{n=-\infty }^{\infty }{F}_n{e}^{jn\Omega t}$$

• 系统零状态响应:
  $$\begin{array}{rl}y(t)=h(t)\star f_T(t)& =\sum _{n=-\infty }^{\infty }{F}_n[h(t)\star e^{jn\Omega t}]\\ \{e^{jn\Omega t}\to \boxed{h(t)}\to H(jn\Omega )\cdot e^{jn\Omega t}\}& =\sum _{n=-\infty }^{\infty }{F}_{n}H(jn\Omega )e^{jn\Omega t}\\ & =\sum _{n=-\infty }^{\infty }{Y}_n{e}^{jn\Omega t}\end{array}$$

  $$F_n\to \boxed{H(jn\Omega )}\to Y_n=F_n\cdot H(jn\Omega )$$

• 步骤:

  1. 求周期输入信号 $f_T(t)$ 的傅里叶系数 $F_n$ ;
  2. 求系统频率响应 $H(jn\Omega )=H(j\omega ){|}_{\omega =n\Omega }$ ;
  3. 求零状态响应 $y(t)$ 的傅里叶系数 $Y_n=F_n\cdot H(jn\Omega )$;
  4. 求傅里叶级数展开式 $y(t)={\sum }_{n=-\infty }^{\infty }{F}_{n}H(jn\Omega )e^{jn\Omega t}$ 。

• 周期信号采用三角形式傅里叶级数
  $$f_T(t)=\frac{A_0}{2}+\sum _{n=1}^{\infty }{A}_n\cos (n\Omega t+{\phi }_n)$$

  • 设系统频率响应函数:
    $$H(j\omega )=|H(j\omega )|e^{j\theta (\phi )}$$
    $$H(jn\Omega )=|H(jn\Omega )|e^{j\theta (n\Omega )}=H(j\omega ){|}_{\omega =n\Omega }$$
  • 可推导出:
    $$y(t)=\frac{A_0}{2}\stackrel{\text{直流增益}}{H(0)}+\sum _{n=1}^{\infty }{A}_n\stackrel{\text{幅值相乘}}{|H(jn\Omega )|}\cos [n\Omega t+{\phi }_n\stackrel{\text{相位相加}}{+\theta (n\Omega )}]$$

3.1.4. 频率响应函数

• 频率响应函数 $H(j\omega )$

  • 定义: 系统零状态响应 $y(t)$ 的傅里叶变换 $Y(j\omega )$ 与激励 $f(t)$ 的傅里叶变换 $F(j\omega )$ 之比。即:
    $$H(j\omega )=\frac{Y(j\omega )}{F(j\omega )}$$

  • $H(j\omega )$ 一般为复函数, 记为:
    $$H(j\omega )=|H(j\omega )|e^{j\theta (\omega )}=\frac{|Y(j\omega )|}{|F(j\omega )|}{e}^{j[{\phi }_y(\omega )-{\phi }_f(\omega )]}$$

  • $|H(j\omega )|$ 称为幅频特性(或幅频响应), 是 $\omega$ 的偶函数；

  • $\theta (\omega )$ 称为相频特性(或相频响应), 是 $\omega$ 的奇函数。

• 频率响应函数的求法

  1. $H(j\omega )=\mathfrak{F}[h(t)]$
  2. $H(j\omega )=\frac{Y(j\omega )}{F(j\omega )}$
     1. 由电路的频域模型直接求出;
     2. 由微分方程求出, 对微分方程两边取傅里叶变换。

3.1.5. Python 求解系统响应

• 已知系统的频率响应函数和输入分别为:
  $$H(j\omega )=\frac{1-j\omega }{1+j\omega },f(t)=\sin (t)+\sin (3t)$$
  • 用 Python 求解系统响应

    # 导入 需要的 library 库  
    import numpy as np # 科学计算
    import matplotlib.pyplot as plt # 画图工具
    import scipy.signal as sg # 导入 scipy 的 signal 库 重命名为 sg
    
    # 用 Python 表示 
    t = np.linspace(0,4*np.pi,401) 
    a, b = [1,1],[-1,1] # 频率响应函数的分母 分子系数
    ft = np.sin(t) + np.sin(3*t) # 激励
    sys = sg.lti(b,a)
    _,yt,_ = sg.lsim(sys,ft, T= t)
    # 开始绘图
    y1, = plt.plot(t,ft,'--',label=r'$f(t)$') 
    y2, = plt.plot(t,yt,label=r'$y(t)$') 
    plt.legend(handles=[y1,y2], loc='upper right')
    plt.xticks(t[::100],[fr'${int(i/np.pi)}\pi$'for i in t[::100]])
    plt.grid(True)
    plt.show()

---

3.2. 滤波器

3.2.1. 无失真传输

• 系统对于信号的作用大体可分为两类：一类是信号的传输，一类是滤波。传输要求信号尽量不失真，而滤波则要求滤去或削弱不需要的成分，必然伴随着失真。

• 定义:

  • 信号无失真传输是指系统的输出信号与输入信号相比，只有幅度的大小和出现时间的先后不同，而没有波形上的变化。
  • 输入信号 $f(t)$ ，经过无失真传输后，输出信号应为
    $$y(t)=Kf(t-t_d)$$
  • 其频谱关系为
    $$Y(j\omega )=K{e}^{-j\omega t_d}F(j\omega )$$

• 条件:

  1. 对 $h(t)$ 的要求:
     $$h(t)=K\delta (t-t_d)$$
  2. 对 $H(j\omega )$ 的要求:
     $$H(j\omega )=\frac{Y(j\omega )}{F(j\omega )}=K{e}^{-j\omega t_d}$$
     即
     $$|H(j\omega )|=K,\theta (\omega )=-\omega t_d$$

• Remark: 上述是信号无失真传输的理想条件。当传输有限带宽的信号时，只要在信号占有频带范围内，系统的幅频、相频特性满足以上条件即可。

3.2.2. 理想低通滤波器

• (LPF) Low-pass filter
  

• 定义:

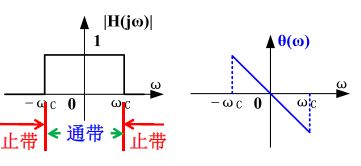
  • 具有如图所示矩形幅频特性、线性相频特性的系统称为理想低通滤波器。
  • ${\omega }_C$ 称为截止角频率
  • 理想低通滤波器的频率响应可写为:
    $$\begin{array}{r}H(j\omega )=\{\begin{array}{ll}{e}^{-j\omega t_d},& |\omega |<{\omega }_C\\ 0,& |\omega |>{\omega }_C\end{array}=g_{2{\omega }_C}(\omega )e^{-j\omega t_d}\end{array}$$
    即:
    $$\begin{array}{rl}|H(j\omega )|& =\{\begin{array}{ll}1,& |\omega |<{\omega }_C\\ 0,& |\omega |>{\omega }_C\end{array}\\ \phi & =-j\omega t_d\end{array}$$

• 冲激响应:
  $$\begin{array}{rl}h(t)& ={\mathfrak{F}}^{-1}[g_{2{\omega }_C}(\omega )e^{-j\omega t_d}]\\ & =\frac{{\omega }_C}{\pi }\text{Sa}[{\omega }_C(t-t_d)]\end{array}$$
  

• 结论

  1. 比较输入输出，可见严重失真
     • 原因: $\delta (t)\leftrightarrow 1$ 信号频带无限宽，理想低通滤波器通频带是有限的， ${\omega }_C$ 以上的频率成分截止。
  2. 理想低通滤波器是物理不可实现的非因果系统

• 阶跃响应:
  $$\begin{array}{rl}g(t)& =h(t)\star \epsilon (t)\\ & ={\int }_{-\infty }^{t}h(\tau )d\tau \\ & =\frac{1}{2}+\frac{1}{\pi }\text{Si}[{\omega }_C(t-t_d)]\end{array}$$

  • 正弦积分:
    $$\text{Si}(y)={\int }_0^y\frac{\sin (x)}{x}dx$$

  • 特点:

    1. 奇函数
    2. 最大值 $\text{Si}(\pi )$
    3. 最小值 $\text{Si}(-\pi )$
    4. 稳态值 $\text{Si}(\infty )=\pi /2$
       

  • 上升时间 ${\tau }_r$ :

    • 输出由最小值到最大值所经历的时间。
      $${\tau }_r=\frac{2\pi }{{\omega }_C}=\frac{1}{B}$$
    • 可见：阶跃响应的上升时间 $t_r$ 与滤波器带宽 $B$ 成反比
      
    • 特点:
      • 有明显失真，只要 ${\omega }_C<\infty$ ，则必有振荡，其过冲比稳态值高约 $9$ 。这一由频率截断效应引起的振荡现象称为吉布斯现象。
        $$g_{\text{max}}=\frac{1}{2}+\frac{1}{\pi }\text{Si}(\pi )\approx 1.0895$$

3.2.3. 物理可实现系统的条件

• 时域特性: 因果条件
  $$h(t)=0,t<0$$

• 频域特性:
  $$\begin{array}{r}\underset{\text{(必要条件)}}{\text{佩利-维纳准则}}\{\begin{array}{ll}& {\int }_{\infty }^{\infty }|H(j\omega ){|}^{2}d\omega <\infty \\ & \text{平方可积条件}\\ & \\ & {\int }_{\infty }^{\infty }\frac{|\ln |H(j\omega )||}{1+{\omega }^2}d\omega <\infty \end{array}\end{array}$$

• Remark：

  1. 物理可实现系统时域特性表明，响应不应在激励作用之前出现；
  2. 对于物理可实现系统,可以允许 $H(j\omega )$ 特性在某些不连续的频率点上为 $0$ ，但不允许在一个有限频带内为 $0$。按此原理，理想低通、理想高通、理想带通、理想带阻等理想滤波器都是不可实现的；
  3. 佩利-维纳准则要求可实现的幅度特性其总的衰减不能过于迅速；
  4. 佩利-维纳准则是系统物理可实现的必要条件，而不是充分条件。

• 几种常见的实际滤波器

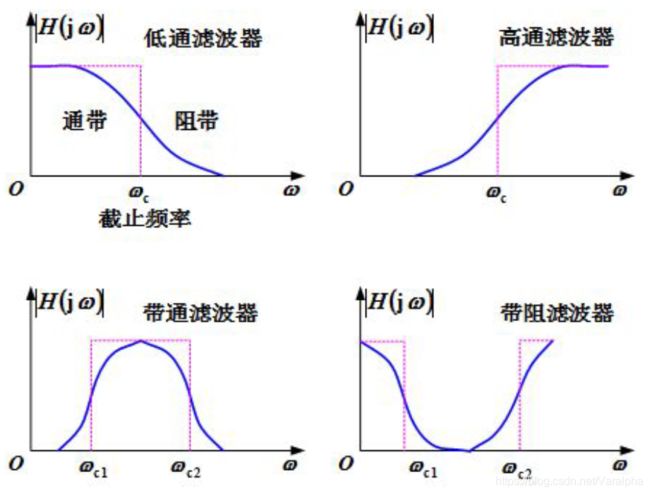
  • $理想滤波器,实际滤波器$
    

To TOP 至目录