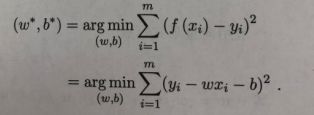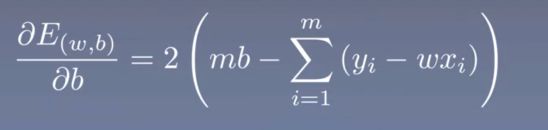AI-西瓜书(1)-一元线性回归公式推导(1)-偏置b
对于实际应用来说,一元线性回归是常用的,实测值、预测值、损失值。为了调参、为了最小化损失,知其然也知其所以然,不能怕麻烦,手推公式。最重要的是理解了背后的数学原理,可以做恒等变形和等价变换,实际应用时,可以使得原来不可解的变为可解的。
原问题:
1.我有实测值表达如下:后面为向量形式
2.yi表示预测值
3.我希望两个相等,或者叫损失值最小,公式表达如下:
步骤:1.求偏置b
2求解权重w
3将w向量化
本文讲第一步,求偏置b的公式推导.
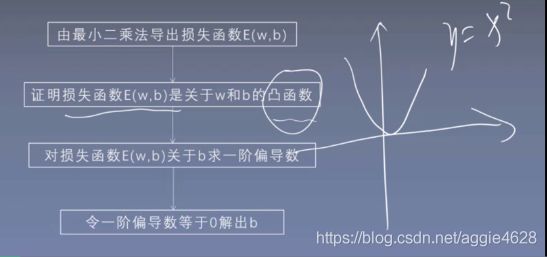
1求解偏置b(4步)
数学原理:二元函数求损失最小,就是最小二乘+一阶偏导求驻点。前提条件:是凸函数。(参看前篇)
驻点:又称为平稳点、稳定点或临界点是函数的一阶导数为零。
最小二乘:二乘就是平方。两个数相减然后平方。
第一步:最小二乘法导出损失函数公式:
Yi –真实值
F(xi)-预测值
第二步:证明损失函数E(w,b)是关于w和b的凸函数:
数学原理:二元函数判断凹凸性,二元函数求最值。
二阶偏导数求法,先求一阶偏导,再求二阶偏导
分别求ABC
A(一阶 二阶)
B(一阶 二阶)
C(一阶 二阶)
AC-B*B
中间一共10步恒等变形与等价转换
第三步:对损失函数E(w,b) 关于b求一阶偏导
第四步:求驻点 一阶偏导
1.2求解权重w
1.3将w向量化
-