基于Centroidal Voronoi Tessellation （CVT）算法的点云三角网格化方法

在之前的博客中，老甘已经跟大家提到过Centroidal Voronoi Tessellation（CVT）算法的实现与可视化。

链接：https://blog.csdn.net/aliexken/article/details/106555993

这里我们来介绍一下基于CVT算法的应用，基于点云数据的三角网格化。

1. 网格化

基于CVT算法的一个非常重要的应用就是针对于点云数据的三角网格化[1][2]。基本的步骤就是首先对点云数据进行均匀重采样，得到一个被优化过的点云。基于优化点云，利用与Voronoi图对偶的Delaunay三角化结果，生成一个近似全局同构的三角网格。这个三角网格因为是基于被优化的点云而生成的，因此该三角化的同构性非常好，网格质量比传统方法要高很多。

基于之前的CVT实现，我实现了该功能，对比传统的Poisson曲面重建方法，结果如下：

 

左图为原始的点云数据，取自Bunny的obj文件。中图为利用Poisson算法对点云数据进行重建，生成网格数据。右图为基于CVT算法生成的三角网格。可以看到，右图的三角网格中，三角形的同构性质更好。同构性好的三角网格，在计算曲面特征的时候更便利，如测地线测算等。

2. CVT对网格的优化

那么我们具体来看一下CVT算法在点云三角网格化这件工作中是如何运行的。首先，我们利用CVT算法对一个不规则的点云数据进行同构优化，最终得到一个同构的点云重采样。在每一步的更新迭代后，点云数据就会更加趋向与同构。下图中展示不同的更新阶段，点云数据的三角网格重建结果：

 

从左到右，CVT更新次数对应为：1，5，10，100。可以看到，整个三角网格的质量随着迭代次数的增加而改善。为了更加方便的查看网格质量，这里我做了一个半边结构的可视化，方便读者更加直观的理解面片的质量。其中左图为poisson重建后的结果，右图为CVT优化后的结果。我们可以非常直观的看到，经过CVT优化的面片，其半边结构的规整度更高。

 

3. CVT在实际使用中的注意事项

这里有三点需要注意：

第一， 相关的参考文献中，声称基于CVT算法的网格重建能够利用并行结构而实现加速。对于CVT更新来说，每次更新都需要对上一次定位的点建立搜索结构来提高紧邻查找效率，那么实际上这个并行结构是要在一次迭代后重新整合的，因此按照我目前的理解，还不能建立全程并行的实现方法。所以随着迭代次数与采样点的增加，时间开销必然会显著增加

第二，这里的三角网格是对每一个点与紧邻计算Voronoi图，进而得到其对偶的Delaunay三角化结果。最后的结果是将所有的点的Delaunay三角化组合起来，进而得到一个三角网格数据。这种三角化难免会出现局部丢失面片的情况，因此在实际使用中的时候，需要去修补面片丢失的区域。

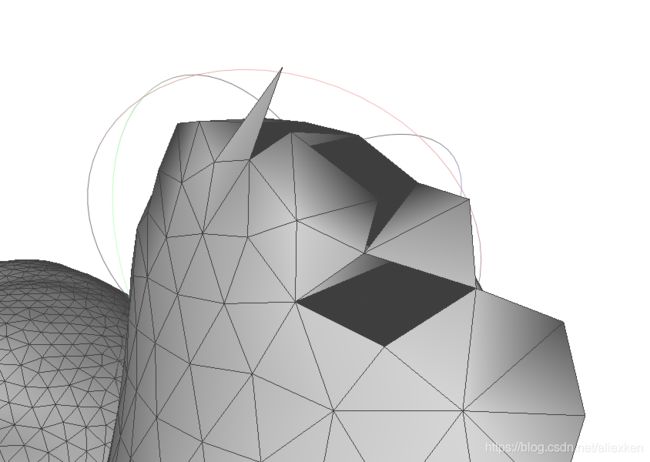
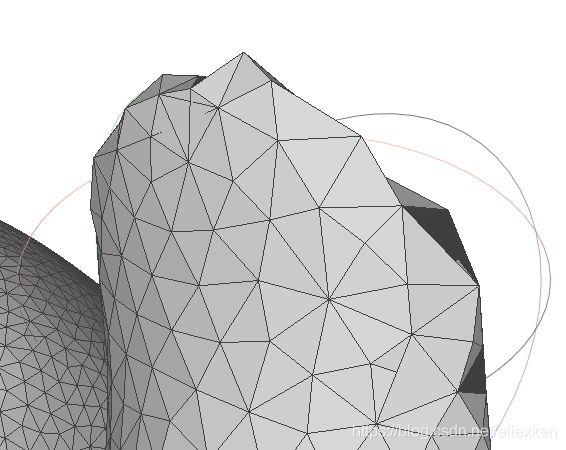
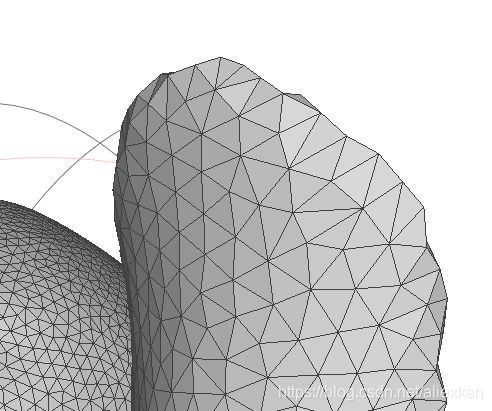
第三，在对每一点进行最近邻查找的时候，在曲率变化sharp的地方，可能会发生错误的连接情况（下图中左图为例）。原因是，最近邻是根据欧氏距离来做的，而不是测地线。一个解决的办法是将法线约束引入紧邻查找，以防止相邻点的错误连接（下图中中图为例）。可以看到错误连接的情况有一定的改善，剩余的孔洞可以通过对边界探查并修补来填充。

有兴趣的各位可以利用我提供的Voronoi图代码，或者CGAL库的功能函数实现看看。

参考文献：

[1] Yan et al. Isotropic Remeshing with Fast and Exact Computation of Restricted Voronoi Diagram, 2009.

[2] Bruno et al. Variational Anisotropic Surface Meshing with Voronoi Parallel Linear Enumeration, 2012.