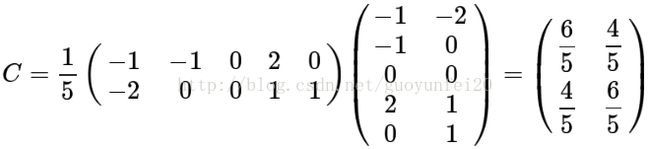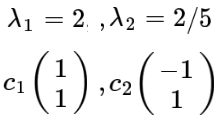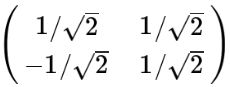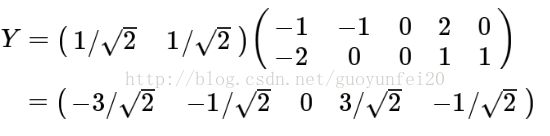主成分分析(principle component analysis)介绍
一、介绍
主成分分析(principal components analysis,PCA)又称主分量分析,主成分回归分析。旨在利用降维的思想,把多指标转化为少数几个综合指标。在统计学中,PCA是一种简化数据集的技术。
它是一个线性变换。这个变换把数据变换到一个新的坐标系统中,使得任何数据投影的第一大方差在第一个坐标(称为第一主成分)上,第二大方差在第二个坐标(第二主成分)上,依次类推。
主成分分析经常用减少数据集的维数,同时保持数据集的对方差贡献最大的特征。
二、原理
PCA是一种降维的统计方法,它借助于一个正交变换,将其分量相关的原随机向量转化成其分量不相关的新随机向量,这在代数上表现为将原随机向量的协方差阵变换成对角形阵,在几何上表现为将原坐标系变换成新的正交坐标系,使之指向样本点散布最开的p 个正交方向,然后对多维变量系统进行降维处理,使之能以一个较高的精度转换成低维变量系统,再通过构造适当的价值函数,进一步把低维系统转化成一维系统。
PCA的原理是设法将原来变量重新组合成一组新的相互无关的几个综合变量,同时根据实际需要从中可以取出几个较少的总和变量尽可能多地反映原来变量的信息的统计方法,是数学上处理降维的一种方法。
三、计算步骤
设样本数据为n维,共m个。
1、将这些样本数据按列组成矩阵Xnm
2、对X按行均值化,即先求每一行的均值,然后该行的每一个元素都减去这个均值
4、求出协方差矩阵的特征值即对应的特征向量
5、将特征向量按对应的特征值的大小,从时而下按行排列成矩阵,取前k行组成矩阵P
6、则Y = PX即为降维到k维后的数据集。
举例:
原始数据为2维,有5个数据。组成的矩阵为:
我们的任务是将这个2维的数据集降到1维。
首先按行均值化,由于我们举例的数据如此简单,你会发现均值化后的矩阵不变哈!
接下来去协方差矩阵:
接下来去C的特征值和特征向量(此处略,可参考线性代数)结果为:
特征向量时通解,c1和c2可取任意非零实数。标准化后的特征向量为:
按特征值由大到小,将对应的特征向量按行由上往下写,得到矩阵:
由于我们要降到1维,即选取第一个主成分,即选取第一行,于是有:
四、用OpenCV 3.3 计算PCA
在OpenCV3.3版本中,在core.hpp文件中定义了类cv::PCA Class用于计算PCA。通常的用法如下:
using namespace cv;
PCA compressPCA(const Mat& pcaset, // 输入的数据集,其PCA结果由return给出
int maxComponents, // 主成分的个数,如果数据时n维的,则主成分要<=n
const Mat& testset, // 测试数据集
Mat& compressed) // 测试数据集的PCA的结果
{
// 定义PCA类对象,调用了带参数的构造函数(直线构造函数时就计算出了主成分)
PCA pca(pcaset, // pass the data
Mat(), // we do not have a pre-computed mean vector,so let the PCA engine to compute it
PCA::DATA_AS_ROW, // indicate that the vectors are stored as matrix rows
// 即每一行为一个样本,样本的维数为pcaset.cols,共pcaset.rows个样本
maxComponents); // specify, how many principal components to retain
// if there is no test data, just return the computed basis, ready-to-use
if( !testset.data )
return pca;
CV_Assert( testset.cols == pcaset.cols );
compressed.create(testset.rows, maxComponents, testset.type());
Mat reconstructed;
for( int i = 0; i < testset.rows; i++ )
{
Mat vec = testset.row(i), coeffs = compressed.row(i), reconstructed;
// compress the vector, the result will be stored in the i-th row of the output matrix
pca.project(vec, coeffs);
// and then reconstruct it
pca.backProject(coeffs, reconstructed);
// and measure the error
printf("%d. diff = %g\n", i, norm(vec, reconstructed, NORM_L2));
}
return pca;
}https://docs.opencv.org/3.1.0/d1/dee/tutorial_introduction_to_pca.html下边贴出代码:
#include
#include
using namespace std;
using namespace cv;
// Function declarations
void drawAxis(Mat&, Point, Point, Scalar, const float);
double getOrientation(const vector &, Mat&);
// 画坐标轴(带箭头的直线)
void drawAxis( Mat& img,
Point p, // from start point
Point q, // to end point
Scalar colour, const float scale = 0.2)
{
double angle;
double hypotenuse;
angle = atan2( (double) p.y - q.y, (double) p.x - q.x ); // angle in radians
hypotenuse = sqrt( (double) (p.y - q.y) * (p.y - q.y) + (p.x - q.x) * (p.x - q.x));
// Here we lengthen the arrow by a factor of scale
q.x = (int) (p.x - scale * hypotenuse * cos(angle));
q.y = (int) (p.y - scale * hypotenuse * sin(angle));
line(img, p, q, colour, 1, CV_AA);
// create the arrow hooks
p.x = (int) (q.x + 9 * cos(angle + CV_PI / 4));
p.y = (int) (q.y + 9 * sin(angle + CV_PI / 4));
line(img, p, q, colour, 1, CV_AA);
p.x = (int) (q.x + 9 * cos(angle - CV_PI / 4));
p.y = (int) (q.y + 9 * sin(angle - CV_PI / 4));
line(img, p, q, colour, 1, CV_AA);
}
// PCA
double getOrientation(const vector &pts, Mat &img)
{
//! [pca]
//Construct a buffer used by the pca analysis
int sz = static_cast(pts.size());
Mat data_pts = Mat(sz, 2, CV_64FC1);
for (int i = 0; i < data_pts.rows; ++i)
{
data_pts.at(i, 0) = pts[i].x;
data_pts.at(i, 1) = pts[i].y;
}
//Perform PCA analysis
PCA pca_analysis(data_pts, Mat(), CV_PCA_DATA_AS_ROW);
//Store the center of the object
Point cntr = Point(static_cast(pca_analysis.mean.at(0, 0)),
static_cast(pca_analysis.mean.at(0, 1)));
//Store the eigenvalues and eigenvectors
vector eigen_vecs(2);
vector eigen_val(2);
for (int i = 0; i < 2; ++i)
{
eigen_vecs[i] = Point2d(pca_analysis.eigenvectors.at(i, 0),
pca_analysis.eigenvectors.at(i, 1));
eigen_val[i] = pca_analysis.eigenvalues.at(i);
}
//! [pca]
//! [visualization]
// Draw the principal components
circle(img, cntr, 3, Scalar(255, 0, 255), 2);
Point p1 = cntr + 0.02 * Point(static_cast(eigen_vecs[0].x * eigen_val[0]), static_cast(eigen_vecs[0].y * eigen_val[0]));
Point p2 = cntr - 0.02 * Point(static_cast(eigen_vecs[1].x * eigen_val[1]), static_cast(eigen_vecs[1].y * eigen_val[1]));
drawAxis(img, cntr, p1, Scalar(0, 255, 0), 1);
drawAxis(img, cntr, p2, Scalar(255, 255, 0), 5);
double angle = atan2(eigen_vecs[0].y, eigen_vecs[0].x); // orientation in radians
//! [visualization]
return angle;
}
int main(int argc, char** argv)
{
//! [pre-process]
// Load image
String imageName("./pca_test1.jpg"); // by default
if (argc > 1)
{
imageName = argv[1];
}
Mat src = imread( imageName );
// Check if image is loaded successfully
if(!src.data || src.empty())
{
cout << "Problem loading image!!!" << endl;
return EXIT_FAILURE;
}
imshow("src", src);
// Convert image to grayscale
Mat gray;
cvtColor(src, gray, COLOR_BGR2GRAY);
// Convert image to binary
Mat bw;
threshold(gray, bw, 50, 255, CV_THRESH_BINARY | CV_THRESH_OTSU);
//! [pre-process]
//! [contours]
// Find all the contours in the thresholded image
vector hierarchy;
vector > contours;
findContours(bw, contours, hierarchy, CV_RETR_LIST, CV_CHAIN_APPROX_NONE);
for (size_t i = 0; i < contours.size(); ++i)
{
// Calculate the area of each contour
double area = contourArea(contours[i]);
// Ignore contours that are too small or too large
if (area < 1e2 || 1e5 < area) continue;
// Draw each contour only for visualisation purposes
drawContours(src, contours, static_cast(i), Scalar(0, 0, 255), 2, 8, hierarchy, 0);
// Find the orientation of each shape
getOrientation(contours[i], src);
}
//! [contours]
imshow("output", src);
waitKey(0);
return 0;
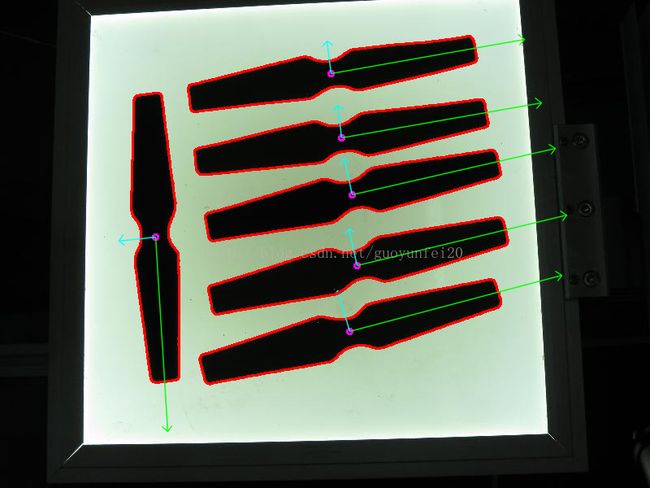
} 运行结果:
绿色线为第一主成分对应的特征向量;青色线为第二主成分对应的特征向量!
https://code.csdn.net/guoyunfei20/pca.git