机器学习课程笔记【五】- 支持向量机(1)
支持向量机算法是最有效的有监督学习算法之一,为全面掌握,首先学习间隔以及数据划分的思想,然后了解最优间隔分类器(涉及拉格朗日对偶,高维特征空间的核函数),最后介绍SVMs的一种高效实现——SMO算法。
本节为支持向量机部分笔记的第一小节,主要内容包括:函数间隔与几何间隔的定义,理想间隔分类器以及拉格朗日对偶问题。
1. 间隔Margins
这一小节主要讨论决策间隔以及预测的可信度
考虑一个逻辑回归,其中概率 p ( y = 1 ∣ x ; θ ) p(y=1|x;\theta) p(y=1∣x;θ)由 h θ ( x ) = g ( θ T x ) h_{\theta}(x)=g(\theta^Tx) hθ(x)=g(θTx)给出,如果 h θ ≥ 0.5 h_{\theta} \geq 0.5 hθ≥0.5则输出类别为“1”。且 θ T x ≥ 0 \theta^Tx \geq 0 θTx≥0时,越大说明我们的预测的可信度也就越高,如下图所示:
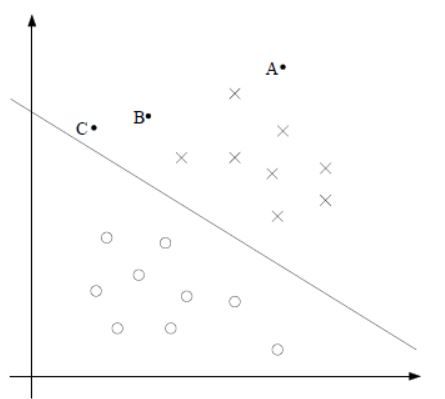
我们预测A为“x”类自然要比预测C为“x”类的可信度要高,因为决策边界的轻微变化,C的类别可能就会变。
2. 一种新的符号记法
为了简化对SVMs的讨论,在谈分类这一事情的时候我们引入一种新的记法。考虑特征 x x x标签为 y y y的二类问题的线性分类器,标签 y ∈ { − 1 , 1 } y \in \{-1,1\} y∈{−1,1}(不再是 { 0 , 1 } \{0,1\} {0,1}),并且使用参数 w , b w,b w,b来代替 θ \theta θ,这样我们的分类器可以写为:
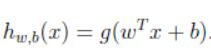
其中,当 z ≥ 0 z \geq 0 z≥0时函数 g ( z ) = 1 g(z)=1 g(z)=1,其他情况函数取-1。
3. 函数间隔与几何间隔
这里给出函数间隔和集合间隔的形式化定义。给定训练样本 ( x ( i ) , y ( i ) ) (x^{(i)},y^{(i)}) (x(i),y(i)),定义 ( w , b ) (w,b) (w,b)对于训练样本的函数间隔为:
![]()
这里如果 y ( i ) = 1 y^{(i)}=1 y(i)=1,要使得函数间隔大那 ω T x + b \omega^Tx+b ωTx+b的值也应为一个尽可能大的正数;若 y ( i ) = − 1 y^{(i)}=-1 y(i)=−1,要使得函数间隔大那 ω T x + b \omega^Tx+b ωTx+b的值应为一个尽可能小的负数。如果这个函数间隔的值为正,那么我的预测就是正确的。所以说,大函数间隔代表了可行度更高的正确预测。
然而函数间隔的一个特性使得其定义可信度存在一些问题,比如给定一个 g g g,如果 ω → 2 ω , b → 2 b \omega \rightarrow 2\omega,b \rightarrow 2b ω→2ω,b→2b,会使函数间隔变大两倍,通过这样的调整可以使得函数间隔任意大,但并没有什么有意义的改变。这就涉及到了归一化的定义,比如 ∣ ∣ ω ∣ ∣ 2 = 1 ||\omega||_2=1 ∣∣ω∣∣2=1,我们可以令 ( ω , b ) → ( ω / ∣ ∣ ω ∣ ∣ 2 , b / ∣ ∣ ω ∣ ∣ 2 ) (\omega,b)\rightarrow (\omega/||\omega||_2,b/||\omega||_2) (ω,b)→(ω/∣∣ω∣∣2,b/∣∣ω∣∣2),归一化的问题之后会再提到,所以这里先略过继续往下。
给定训练集S:
![]()
定义对于训练集S, ( ω , b ) (\omega,b) (ω,b)的函数间隔为所有训练样本中最小的一个函数间隔,记为:
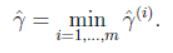
然后来看几何间隔,如下图所示:
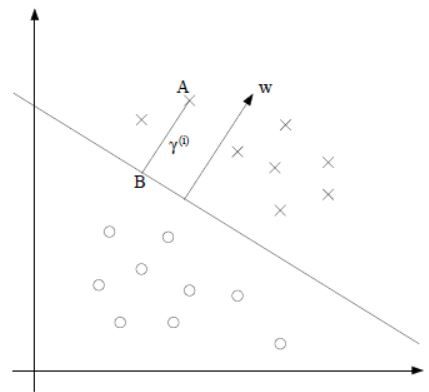
决策边界给出,考虑训练集中的输入 x ( i ) x^{(i)} x(i)也即点A,它与决策边界的距离就是线段AB,那如何确定这个线段AB?
首先我们可以定位点B,它可以由下式给出,其中 ω / ∣ ∣ ω ∣ ∣ \omega/||\omega|| ω/∣∣ω∣∣为单位向量:
![]()
但是这个点正好在决策边界上,决策边界上的点都有:
![]()
因此有:
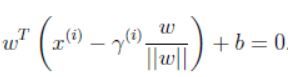
从而得到A对应的样本的函数间隔:

在此基础上定义单个样本的几何间隔为:
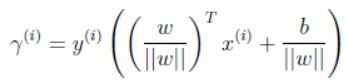
这里,如果 ∣ ∣ ω ∣ ∣ = 1 ||\omega||=1 ∣∣ω∣∣=1,那么函数间隔和几何间隔相等,而且几何间隔对参数的缩放无关。也就是说对参数进行拟合的时候我们可以任取参数的一个数量级还不用进行缩放。
最后,训练集的几何间隔也有:
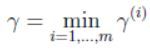
4. 理想间隔分类器
经过上面的讨论,给定一个数据集,那么最迫切的任务就是找到一个决策边界来最大化几何间隔。
当前我们假定训练集都是线性可分的,也就是说能用某个分离超平面来将正类和负类分开。我们怎样确定这个超平面来使得几何间隔最大,也就自然的引出了如下优化问题:
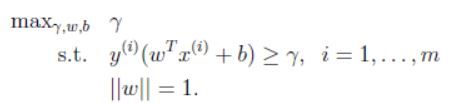
我们想要最大化训练样本的最小函数间隔,而 ∣ ∣ ω ∣ ∣ = 1 ||\omega||=1 ∣∣ω∣∣=1则保证了函数间隔和几何间隔相同,也就是说我们最大化的也是最小几何间隔。
这样如果我们解决了优化问题,所有问题就解决了,然而" ∣ ∣ ω ∣ ∣ = 1 ||\omega||=1 ∣∣ω∣∣=1"这个约束条件是一个非凸约束,没有一个常规的标准优化算法能对其进行求解,所以我们将问题转化成一个易于解决的,考虑:

这里我们最大化 γ ^ / ∣ ∣ ω ∣ ∣ \hat \gamma /||\omega|| γ^/∣∣ω∣∣,并且使得所有的函数间隔最小为 γ ^ \hat \gamma γ^,因为几何间隔和函数间隔通过式子 γ = γ ^ / ∣ ∣ ω ∣ ∣ \gamma=\hat \gamma /||\omega|| γ=γ^/∣∣ω∣∣相联系,至此我们就拜托了这个非凸的约束条件,然而却多了一个非凸的约束目标函数,这里我们仍然没有好的方法处理。
继续来看,之前我们讨论过同时对 ω , b \omega,b ω,b施加一个缩放因子并不会改变模型,这里我们用到这个关键思想。引入缩放因子使得 ( w , b ) (w,b) (w,b)为1即 γ ^ = 1 \hat \gamma =1 γ^=1。
然后最大化 γ ^ / ∣ ∣ ω ∣ ∣ \hat \gamma /||\omega|| γ^/∣∣ω∣∣就是最大化 1 / ∣ ∣ ω ∣ ∣ 1/||\omega|| 1/∣∣ω∣∣,也就是最小化 ∣ ∣ ω ∣ ∣ 2 ||\omega||^2 ∣∣ω∣∣2,问题也转化为如下优化问题:

这个优化问题就很容易求解了,凸函数+线性约束。该问题的解就是我们要求的理想间隔分类器。
接下来的一节将讨论我们优化问题的对偶形式,这将在高维空间中高效通过和函数获得理想间隔分类器中意义重大,对偶形式还能使得我们推导出一个比通用的二次规划更好的方法来解决上述的优化问题。
5. 拉格朗日对偶
这一节先讨论一下约束最优化问题的求解。
考虑这样一个优化问题:

这里要用到拉格朗日乘子法,定义:
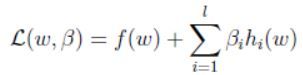
其中 β i ′ s \beta_i's βi′s被称为拉格朗日乘子。令上式偏导为0,有:
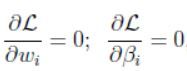
然后解出 ω , β \omega,\beta ω,β。这一节我们将把这个问题推广至一般的线性最优化问题,约束条件可能是不等式约束也有可能是等式约束,如下:
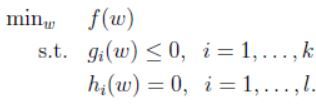
这里定义一个一般形式的格拉朗日乘子式:
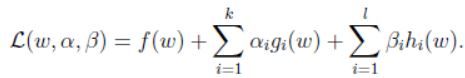
其中 α i ′ s \alpha_i's αi′s和 β i ′ s \beta_i's βi′s分别为拉格朗日乘子,考虑下面的量:
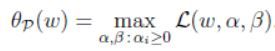
这里下标 P \Rho P表示“primal”,给定 ω \omega ω,如果它违反了原始的约束条件,那么有:
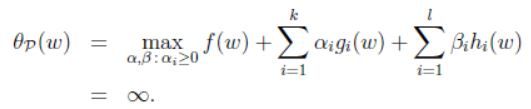
相反,如果约束条件确实满足,那么有:
![]()
因此有:

如果我们考虑这样的一个最小化问题:
![]()
它和我们原始的问题是相同的,这里定义一个新的优化目标以备后用:
![]()
然后定义原始问题的对偶形式,首先定义(D for Dual):
![]()
然后定义对偶的优化问题:
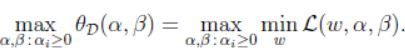
这里和原始问题相同只不过max和min的顺序相反,同样地,定义对偶问题的优化目标:
![]()
原始问题和其对偶性是的联系可以由下面的式子给出:

可以看出在某些特定条件下,我们可以得到:
![]()
这样我们找到这个特定条件,那么我们就可以通过解决对偶问题来解决原始问题,下面的重点变为找到这个等式成立的条件。
假如 f f f和 g i ′ s g_i's gi′s都是凸函数, h i ′ s h_i's hi′s是仿射的(仿射和线性的意思大致相同,只不过允许一个额外的截距),假设 g i g_i gi可行,意味着存在某个 ω \omega ω使得对所有的 i i i,都有 g i ( ω ) < 0 g_i(\omega)<0 gi(ω)<0成立。
在以上假设成立的前提下,必然存在 ω ∗ , α ∗ , β ∗ \omega^*,\alpha^*,\beta^* ω∗,α∗,β∗使得 ω ∗ \omega^* ω∗是原始问题的解, α ∗ , β ∗ \alpha^*,\beta^* α∗,β∗是对偶问题的解并且:
![]()
此外, ω ∗ , α ∗ , β ∗ \omega^*,\alpha^*,\beta^* ω∗,α∗,β∗也满足Karush-Kuhn-Tucker(KKT)条件,也就是:
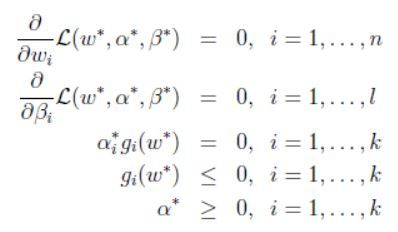
也就是说如果这三个参数满足KKT条件,那么他们就是原始问题和对偶问题的解。其中上图中的第三行公式,也称为KKT对偶补充条件,这个条件后续还有用处。
欢迎扫描二维码关注微信公众号 深度学习与数学 [每天获取免费的大数据、AI等相关的学习资源、经典和最新的深度学习相关的论文研读,算法和其他互联网技能的学习,概率论、线性代数等高等数学知识的回顾]
![]()