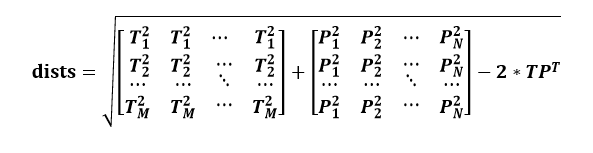计算矩阵的欧式距离
对于kNN算法,难点在于计算测试集中每一样本到训练集中每一样本的欧氏距离,即计算两个矩阵之间的欧氏距离。现就计算欧式距离提出三种方法。
欧式距离:https://baike.baidu.com/item/欧几里得度量/1274107?fromtitle=欧式距离&fromid=2809635&fr=aladdin
1. 两层循环
分别对训练集和测试集中的数据进行循环遍历,计算每两个样本之间的欧式距离。此算法没有经过任何优化。
import numpy as np
matrix_1 = np.array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
matrix_2 = np.array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9],
[3, 2, 1],
[6, 5, 4],
[9, 8, 7]])
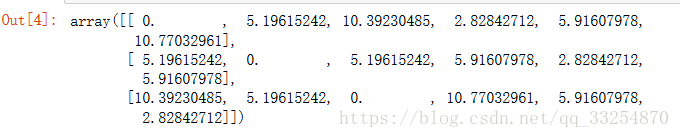
def compute_distances_two_loop(test_matrix, train_matrix):
num_test = test_matrix.shape[0]
num_train = train_matrix.shape[0]
dists = np.zeros((num_test, num_train)) # shape(num_test, num-train)
for i in range(num_test):
for j in range(num_train):
# corresponding element in Numpy Array can compute directly,such as plus, multiply
dists[i][j] = np.sqrt(np.sum(np.square(test_matrix[i] - train_matrix[j])))
return dists
compute_distances_two_loop(matrix_1, matrix_2)
2. 一层循环
利用Numpy广播机制(参见下一篇博客)对方法一进行优化,使用一层循环。
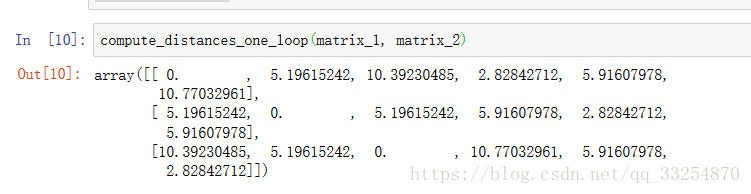
def compute_distances_one_loop(test_matrix, train_matrix):
num_test = test_matrix.shape[0]
num_train = train_matrix.shape[0]
dists = np.zeros((num_test, num_train))
for i in range(num_test):
dists[i] = np.sqrt(np.sum(np.square(test_matrix[i] - train_matrix), axis=1))
# 注:这里用到了广播机制,test_matrix[i]维度为(3,),train_matrix维度为(6, 3),
# 计算结果维度为(6, 3),表示 test_matrix[i] 与 train_matrix 各个样本在各个轴的差值,
# 最后平方后在axis=1维度进行求和。
return dists
compute_distances_one_loop(matrix_1, matrix_2)
3. 不使用循环
计算效率最高的算法是将训练集和测试集都使用矩阵表示,然后使用矩阵运算的方法替代之前的循环操作。但矩阵运算要求我们对矩阵的运算规则非常熟悉。现就计算两个矩阵之间的欧式距离的矩阵运算进行推导。
矩阵之间的欧式距离物理意义:测试集每个样本与训练集每个样本的L2范式。 显然,最后的结果维度应该是(num_test, num_train)。
假设测试集矩阵T的大小为MD,训练集矩阵P的大小为ND(测试集中共有M个点,每个点为D维特征向量;训练集中共有N个点,每个点为D维特征向量)。
记Ti是测试集矩阵T的第i行,Pj是训练集矩阵P的第j行。
具体实现见下:
def non_loop(test_matrix, train_matrix):
num_test = test_matrix.shape[0]
num_train = train_matrix.shape[0]
dists = np.zeros((num_test, num_train))
# because(X - X_train)*(X - X_train) = -2X*X_train + X*X + X_train*X_train, so
d1 = -2 * np.dot(test_matrix, train_matrix.T) # shape (num_test, num_train)
d2 = np.sum(np.square(test_matrix), axis=1, keepdims=True) # shape (num_test, 1)
d3 = np.sum(np.square(train_matrix), axis=1) # shape (num_train, )
dists = np.sqrt(d1 + d2 + d3) # broadcasting
return dists
non_loop(matrix_1, matrix_2)