相似度计算之Jaccard系数
Jaccard相似系数
定义
给定两个集合A,B,Jaccard 系数定义为A与B交集的大小与A与B并集的大小的比值,定义如下:
当集合A,B都为空时,J(A,B)定义为1。
与Jaccard 系数相关的指标叫做Jaccard 距离,用于描述集合之间的不相似度。Jaccard 距离越大,样本相似度越低。公式定义如下:
其中对参差(symmetric difference)
![]()
性质
![]()
实例
主要用于计算符号度量或布尔值度量的个体间的相似度,因为个体的特征属性都是由符号度量或者布尔值标识,因此无法衡量差异具体值的大小,只能获得“是否相同”这个结果,所以Jaccard系数只关心个体间共同具有的特征是否一致这个问题。
1、如果比较X与Y的Jaccard相似系数,只比较xn和yn中相同的个数,公式如下:
如集合A={1,2,3,4};B={3,4,5,6};
那么他们的J(X,Y)=1{3,4}/1{1,2,3,4,5,6}=1/3;
2、样本A与样本B是两个n维向量,而且所有维度的取值都是0或1。例如:A(0111)和B(1011)。我们将样本看成是一个集合,1表示集合包含该元素,0表示集合不包含该元素。
概念浅析:假设A是坚果Pro2 , B是 苹果8x。 为了比较两个手机,给出了n个评价指标,即n维特征,也就是n维向量:1-是国产、2-有刘海、3-价格高于5000。那么对于A=(100),B=(011)。所以,n维向量指样本的N维特征,组成一个集合。而集合是由元素组成的,在对应的特征位置,如果样本有该特征,这个位置集合值取1,表示包含该元素;否则,取0,表示不包含该元素。可见,元素=特征。
P:样本A与B都是1的维度的个数
q:样本A是1,样本B是0的维度的个数
r:样本A是0,样本B是1的维度的个数
s:样本A与B都是0的维度的个数
那么样本A与B的杰卡德相似系数可以表示为:
这里p+q+r可理解为A与B的并集的元素个数,而p是A与B的交集的元素个数。
而样本A与B的杰卡德系数表示为: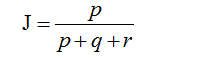
代码
1、当两个集合元素个数相同,则直接调包
from numpy import *
import scipy.spatial.distance as dist # 导入scipy距离公式
matV = mat([[1,1,0,1,0,1,0,0,1],[0,1,1,0,0,0,1,1,1]])
print ("dist.jaccard:", dist.pdist(matV,'jaccard'))2、当集合元素个数不同
def correlation(set_a,set_b):
unions = len(set_a.union(set_b))
intersections = len(set_a.intersection(set_b))
return 1. * intersections / unions