Python面试——数据结构（二）

数据结构

数据结构就是研究数据的逻辑结构和物理结构以及它们之间相互关系，并对这种结构定义相应的运算，而且确保经过这些运算后所得到的新结构仍然是原来的结构类型。

• 逻辑结构：数据之间的相互关系。

  • 集合 结构中的数据元素除了同属于一种类型外，别无其它关系。
  • 线性结构 数据元素之间一对一的关系
  • 树形结构 数据元素之间一对多的关系
  • 图状结构或网状结构 结构中的数据元素之间存在多对多的关系

• 物理结构/存储结构：数据在计算机中的表示。物理结构是描述数据具体在内存中的存储（如：顺序结构、链式结构、索引结构、哈希结构）等

• 在数据结构中,从逻辑上可以将其分为线性结构和非线性结构

• 数据结构的基本操作的设置的最重要的准则是,实现应用程序与存储结构的独立。实现应用程序是“逻辑结构”，存储的是“物理结构”。逻辑结构主要是对该结构操作的设定，物理结构是描述数据具体在内存中的存储（如：顺序结构、链式结构、索引结构、希哈结构）等。

• 顺序存储结构中，线性表的逻辑顺序和物理顺序总是一致的。但在链式存储结构中，线性表的逻辑顺序和物理顺序一般是不同的。

• 时间复杂度：算法的执行时间与原操作执行次数之和成正比。时间复杂度有小到大：O(1)、O(logn)、O(n)、O(nlogn)、O(n2)、O(n3)。幂次时间复杂度有小到大O(2n)、O(n!)、O(nn)

• 空间复杂度：若输入数据所占空间只取决于问题本身，和算法无关，则只需要分析除输入和程序之外的辅助变量所占额外空间。

线性表

线性表是一种典型的线性结构。头结点无前驱有一个后继，尾节点无后继有一个前驱。链表只能顺序查找，定位一个元素的时间为O(N)，删除一个元素的时间为O(1)

1. 线性表的顺序存储结构：把线性表的结点按逻辑顺序依次存放在一组地址连续的存储单元里。用这种方法存储的线性表简称顺序表。是一种随机存取的存储结构。顺序存储指内存地址是一块的，随机存取指访问时可以按下标随机访问，存储和存取是不一样的。如果是存储，则是指按顺序的，如果是存取，则是可以随机的，可以利用元素下标进行。数组比线性表速度更快的是：原地逆序、返回中间节点、选择随机节点。
   • 便于线性表的构造和任意元素的访问
   • 插入：插入新结点，之后结点后移。平均时间复杂度:O(n)
   • 删除：删除节点，之后结点前移。平均时间复杂度:O(n)
2. 线性链表：用一组任意的存储单元来依次存放线性表的结点，这组存储单元即可以是连续的，也可以是不连续的，甚至是零散分布在内存中的任意位置上的。因此，链表中结点的逻辑次序和物理次序不一定相同。为了能正确表示结点间的逻辑关系，在存储每个结点值的同时，还必须存储指示其后继结点的地址。data域是数据域，用来存放结点的值。next是指针域（亦称链域），用来存放结点的直接后继的地址（或位置）。不需要事先估计存储空间大小。
   • 单链表中每个结点的存储地址是存放在其前趋结点next域中，而开始结点无前趋，故应设头指针head指向开始结点。同时，由于最后一个结点无后继，故结点的指针域为空，即NULL。头插法建表(逆序)、尾插法建表(顺序)。增加头结点的目的是算法实现上的方便，但增大了内存开销。
     • 查找：只能从链表的头指针出发，顺链域next逐个结点往下搜索，直到搜索到第i个结点为止。因此，链表不是随机存取结构。
     • 插入：先找到表的第i-1的存储位置，然后插入。新结点先连后继，再连前驱。
     • 删除：首先找到ai-1的存储位置p。然后令p–>next指向ai的直接后继结点，即把ai从链上摘下。最后释放结点ai的空间.r=p->next;p->next=r->next;delete r。
     • 判断一个单向链表中是否存在环的最佳方法是快慢指针。
   • 静态链表：用一维数组来实现线性链表，这种用一维数组表示的线性链表，称为静态链表。静态：体现在表的容量是一定的。（数组的大小）；链表：插入与删除同前面所述的动态链表方法相同。静态链表中指针表示的是下一元素在数组中的位置。
   • 静态链表是用数组实现的，是顺序的存储结构，在物理地址上是连续的，而且需要预先分配大小。动态链表是用申请内存函数（C是malloc,C++是new）动态申请内存的，所以在链表的长度上没有限制。动态链表因为是动态申请内存的，所以每个节点的物理地址不连续，要通过指针来顺序访问。静态链表在插入、删除时也是通过修改指针域来实现的，与动态链表没有什么分别
   • 循环链表：是一种头尾相接的链表。其特点是无须增加存储量，仅对表的链接方式稍作改变，即可使得表处理更加方便灵活。
     • 在单链表中，将终端结点的指针域NULL改为指向表头结点的或开始结点，就得到了单链形式的循环链表，并简单称为单循环链表。由于循环链表中没有NULL指针，故涉及遍历操作时，其终止条件就不再像非循环链表那样判断p或p—>next是否为空，而是判断它们是否等于某一指定指针，如头指针或尾指针等。
   • 双向链表:在单链表的每个结点里再增加一个指向其直接前趋的指针域prior。这样就形成的链表中有两个方向不同的链。双链表一般由头指针唯一确定的，将头结点和尾结点链接起来构成循环链表，并称之为双向链表。设指针p指向某一结点，则双向链表结构的对称性可用下式描述：p—>prior—>next=p=p—>next—>prior。从两个方向搜索双链表，比从一个方向搜索双链表的方差要小。
     • 插入：先搞定插入节点的前驱和后继，再搞定后结点的前驱，最后搞定前结点的后继。
     • 在有序双向链表中定位删除一个元素的平均时间复杂度为O(n)
     • 可以直接删除当前指针所指向的节点。而不需要像单向链表中，删除一个元素必须找到其前驱。因此在插入数据时，单向链表和双向链表操作复杂度相同，而删除数据时，双向链表的性能优于单向链表

单链表翻转：https://blog.csdn.net/gongliming_/article/details/88712221

class Node(object):
    def __init__(self, elem, next_=None):
        self.elem = elem
        self.next = next_
 
def reverseList(head):
    if head == None or head.next==None:  # 若链表为空或者仅一个数就直接返回
        return head 
    pre = None
    next = None
    while(head != None): 
        next = head.next     # 1
        head.next = pre     # 2
        pre = head      # 3
        head = next      # 4
    return pre

if __name__ == '__main__':
    l1 = Node(3)    # 建立链表3->2->1->9->None
    l1.next = Node(2)
    l1.next.next = Node(1)
    l1.next.next.next = Node(9)
    l = reverseList(l1)
    print (l.elem, l.next.elem, l.next.next.elem, l.next.next.next.elem)

 

栈和队列

栈

栈(Stack)是限制在表的一端进行插入和删除运算的线性表，通常称插入、删除的这一端为栈顶(Top)，另一端为栈底(Bottom)。先进后出。top= -1时为空栈，top=0只能说明栈中只有一个元素，并且元素进栈时top应该自增

1. 顺序存储栈：顺序存储结构（数组实现）
2. 链栈：链式存储结构（单链表实现）。插入和删除操作仅限制在链头位置上进行。栈顶指针就是链表的头指针。通常不会出现栈满的情况。 不需要判断栈满但需要判断栈空。
3. 两个栈共用静态存储空间,对头使用也存在空间溢出问题。栈1的底在v[1]，栈2的底在V[m]，则栈满的条件是top[1]+1=top[2]。
4. 基本操作：删除栈顶元素、判断栈是否为空以及将栈置为空栈等
5. 对于n各元素的入栈问题，可能的出栈顺序有C(2n,n)/(n+1)个。
6. 堆栈溢出一般是循环的递归调用、大数据结构的局部变量导致的

应用，代码：

1）利用栈反转字符串

# 利用栈将字串的字符反转
def revstring(mystr):
    # your code here
    s = Stack()
    outputStr = ''
    for c in mystr:
        s.push(c)
    while not s.isEmpty():
        outputStr += s.pop()
    return outputStr

2）利用栈判断括号平衡

# 利用栈判断括号平衡Balanced parentheses
def parChecker(symbolString):
    s = Stack()
    balanced = True
    index = 0
    while index < len(symbolString) and balanced:
        symbol = symbolString[index]
        if symbol in '([{':
            s.push(symbol)
        else:
            if s.isEmpty():
                balanced = False
            else:
                top = s.pop()
                if not matches(top, symbol):
                    balanced = False
        index += 1

    if balanced and s.isEmpty():
        return True
    else:
        return False

def matches(open, close):
    opens = '([{'
    closers = ')]}'
    return opens.index(open) == closers.index(close)

3）利用栈将十进制整数转化为二进制数

# 利用栈将十进制整数转化为二进制整数
def Dec2Bin(decNumber):
    s = Stack()

    while decNumber > 0:
        temp = decNumber % 2
        s.push(temp)
        decNumber = decNumber // 2
    binString = ''
    while not s.isEmpty():
        binString += str(s.pop())
    return binString

4）利用栈实现多进制转换

# 利用栈实现多进制转换
def baseConverter(decNumber, base):
    digits = '0123456789ABCDEF'

    s = Stack()

    while decNumber > 0:
        temp = decNumber % base
        s.push(temp)
        decNumber = decNumber // base

    newString = ''
    while not s.isEmpty():
        newString = newString + digits[s.pop()]

    return newString

队列

队列(Queue)也是一种运算受限的线性表。它只允许在表的一端进行插入，而在另一端进行删除。允许删除的一端称为队头(front)，允许插入的一端称为队尾(rear)。先进先出。

1. 顺序队列：顺序存储结构。当头尾指针相等时队列为空。在非空队列里，头指针始终指向队头前一个位置，而尾指针始终指向队尾元素的实际位置

2. 循环队列。在循环队列中进行出队、入队操作时，头尾指针仍要加1，朝前移动。只不过当头尾指针指向向量上界（MaxSize-1）时，其加1操作的结果是指向向量的下界0。除非向量空间真的被队列元素全部占用，否则不会上溢。因此，除一些简单的应用外，真正实用的顺序队列是循环队列。故队空和队满时头尾指针均相等。因此，我们无法通过front=rear来判断队列“空”还是“满”

3. 链队列：链式存储结构。限制仅在表头删除和表尾插入的单链表。显然仅有单链表的头指针不便于在表尾做插入操作，为此再增加一个尾指针，指向链表的最后一个结点。

4. 设尾指针的循环链表表示队列,则入队和出队算法的时间复杂度均为O(1)。用循环链表表示队列，必定有链表的头结点，入队操作在链表尾插入，直接插入在尾指针指向的节点后面，时间复杂度是常数级的；出队操作在链表表头进行，也就是删除表头指向的节点，时间复杂度也是常数级的。

5. 队空条件：rear==front，但是一般需要引入新的标记来说明栈满还是栈空，比如每个位置布尔值

6. 队满条件：(rear+1) % QueueSize==front，其中QueueSize为循环队列的最大长度

7. 计算队列长度：（rear-front+QueueSize）% QueueSize

8. 入队：（rear+1）% QueueSize

9. 出队：（front+1）% QueueSize

10. 假设以数组A[N]为容量存放循环队列的元素,其头指针是front,当前队列有X个元素,则队列的尾指针值为(front+X mod N)

树和二叉树

一种非线性结构。树是递归结构，在树的定义中又用到了树的概念。

基本术语：

1. 树结点：包含一个数据元素及若干指向子树的分支；
2. 孩子结点：结点的子树的根称为该结点的孩子；
3. 双亲结点：B结点是A结点的孩子，则A结点是B结点的双亲；
4. 兄弟结点：同一双亲的孩子结点；
5. 堂兄结点：同一层上结点；
6. 结点层次：根结点的层定义为1；根的孩子为第二层结点，依此类推；
7. 树的高（深）度：树中最大的结点层
8. 结点的度：一个节点含有的子树的个数称为该节点的度
9. 树的度： 一棵树中，最大的节点的度称为树的度。
10. 叶子结点：也叫终端结点，是度为0的结点；
11. 分枝结点：度不为0的结点（非终端结点）；
12. 森林：由m（m>=0）棵互不相交的树的集合称为森林；
13. 有序树：子树有序的树，如：家族树；
14. 无序树：不考虑子树的顺序；

树的种类

•     无序树：树中任意节点的子节点之间没有顺序关系，这种树称为无序树，也称为自由树；
•     有序树：树中任意节点的子节点之间有顺序关系，这种树称为有序树；

          二叉树：每个节点最多含有两个子树的树称为二叉树；
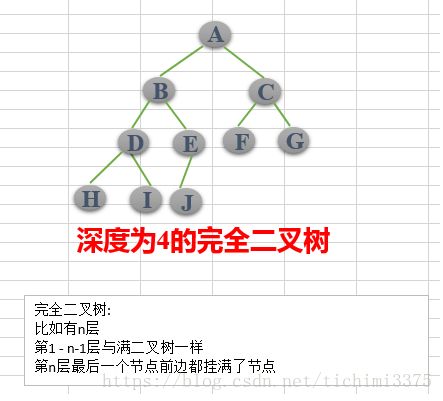
            完全二叉树：对于一颗二叉树，假设其深度为d(d>1)。除了第d层外，其它各层的节点数目均已达最大值，且第d层所有节点从左向右连续地紧密排列，这样的二叉树被称为完全二叉树，其中满二叉树的定义是所有叶节点都在最底层的完全二叉树;
            平衡二叉树（AVL树）：当且仅当任何节点的两棵子树的高度差不大于1的二叉树；
            排序二叉树（二叉查找树（英语：Binary Search Tree），也称二叉搜索树、有序二叉树）；
        霍夫曼树（用于信息编码）：带权路径最短的二叉树称为哈夫曼树或最优二叉树；
        B树：一种对读写操作进行优化的自平衡的二叉查找树，能够保持数据有序，拥有多余两个子树。
 

二叉树

二叉树是每个节点最多有两个子树的树结构。通常子树被称作“左子树”（left subtree）和“右子树”（right subtree）。二叉树可以为空。二叉树结点的子树要区分左子树和右子树，即使只有一棵子树也要进行区分，说明它是左子树，还是右子树。这是二叉树与树的最主要的差别。注意区分：二叉树、二叉查找树/二叉排序树/二叉搜索树、二叉平衡(查找)树

二叉平衡树肯定是一颗二叉排序树。堆不是一颗二叉平衡树。

二叉树与树是不同的，二叉树不等价于分支树最多为二的有序树。当一个结点只包含一个子节点时，对于有序树并无左右孩子之分，而对于二叉树来说依然有左右孩子之分，所以二叉树与树是两种不同的结构。

性质：

性质1: 在二叉树的第i层上至多有2^(i-1)个结点（i>0）
性质2: 深度为k的二叉树至多有2^k - 1个结点（k>0）
性质3: 对于任意一棵二叉树，如果其叶结点数为N0，而度数为2的结点总数为N2，则N0=N2+1;
性质4:具有n个结点的完全二叉树的深度必为 log2(n+1)
性质5:对完全二叉树，若从上至下、从左至右编号，则编号为i 的结点，其左孩子编号必为2i，其右孩子编号必为2i＋1；其双亲的编号必为i/2（i＝1 时为根,除外）

(1)完全二叉树——若设二叉树的高度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第h层有叶子结点，并且叶子结点都是从左到右依次排布，这就是完全二叉树。

(2)满二叉树——除了叶结点外每一个结点都有左右子叶且叶子结点都处在最底层的二叉树。

二叉树的节点表示以及树的创建

通过使用Node类中定义三个属性，分别为elem本身的值，还有lchild左孩子和rchild右孩子

class Node(object):
        """节点类"""
        def __init__(self, elem=-1, lchild=None, rchild=None):
            self.elem = elem
            self.lchild = lchild
            self.rchild = rchild

树的创建,创建一个树的类，并给一个root根节点，一开始为空，随后添加节点

class Tree(object):
        """树类"""
        def __init__(self, root=None):
            self.root = root
     
        def add(self, elem):
            """为树添加节点"""
            node = Node(elem)
            #如果树是空的，则对根节点赋值
            if self.root == None:
                self.root = node
            else:
                queue = []
                queue.append(self.root)
                #对已有的节点进行层次遍历
                while queue:
                    #弹出队列的第一个元素
                    cur = queue.pop(0)
                    if cur.lchild == None:
                        cur.lchild = node
                        return
                    elif cur.rchild == None:
                        cur.rchild = node
                        return
                    else:
                        #如果左右子树都不为空，加入队列继续判断
                        queue.append(cur.lchild)
                        queue.append(cur.rchild)

二叉树的遍历

树的遍历是树的一种重要的运算。所谓遍历是指对树中所有结点的信息的访问，即依次对树中每个结点访问一次且仅访问一次，我们把这种对所有节点的访问称为遍历（traversal）。那么树的两种重要的遍历模式是深度优先遍历和广度优先遍历,深度优先一般用递归，广度优先一般用队列。一般情况下能用递归实现的算法大部分也能用堆栈来实现。
深度优先遍历

对于一颗二叉树，深度优先搜索(Depth First Search)是沿着树的深度遍历树的节点，尽可能深的搜索树的分支。
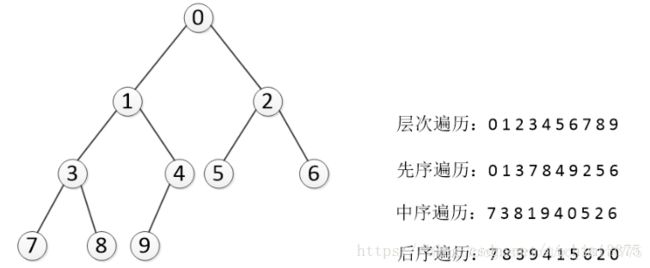
那么深度遍历有重要的三种方法。这三种方式常被用于访问树的节点，它们之间的不同在于访问每个节点的次序不同。这三种遍历分别叫做先序遍历（preorder），中序遍历（inorder）和后序遍历（postorder）。我们来给出它们的详细定义，然后举例看看它们的应用。

    先序遍历 在先序遍历中，我们先访问根节点，然后递归使用先序遍历访问左子树，再递归使用先序遍历访问右子树
    根节点->左子树->右子树

def preorder(self, root):
              """递归实现先序遍历"""
              if root == None:
                  return
              print root.elem
              self.preorder(root.lchild)
              self.preorder(root.rchild)

非递归（需要借助一个堆栈，按照父亲节点、左孩子、右孩子的顺序压到堆里面，每次弹出栈顶元素）：

// 先序
def preorder(root): # 先序
        stack = []
        while stack or root:
            while root:
                print(root.val)
                stack.append(root)
                root = root.lchild
            root = stack.pop()
            root = root.rchild

中序遍历 在中序遍历中，我们递归使用中序遍历访问左子树，然后访问根节点，最后再递归使用中序遍历访问右子树
    左子树->根节点->右子树

def inorder(self, root):
              """递归实现中序遍历"""
              if root == None:
                  return
              self.inorder(root.lchild)
              print root.elem
              self.inorder(root.rchild)

非递归（和先序遍历差不多，区别在于遍历顺序）：

//  中序
def inorder(root): # 中序
        stack = []
        while stack or root:
            while root:
                stack.append(root)
                root = root.lchild
            root = stack.pop()
            print(root.val)
            root = root.rchild

后序遍历 在后序遍历中，我们先递归使用后序遍历访问左子树和右子树，最后访问根节点

    左子树->右子树->根节点

def postorder(self, root):
              """递归实现后续遍历"""
              if root == None:
                  return
              self.postorder(root.lchild)
              self.postorder(root.rchild)
              print root.elem

非递归 ：

方法一

def bin_tree_post_order_traverse2( root):
    '''
    利用一个栈和两个标志节点实现后序遍历
    '''
    curr = root
    prev = None
    s = []
    s.append( curr )
    while s:
        curr = s[-1]
        # 如果当前节点的左节点或者右节点不存在——这个条件针对叶子节点
        #    or 前一个节点是当前节点的左节点或右节点（遍历过了右节点或左节点——这个条件针对非叶子节点
        if ( not curr.lchild and not curr.rchild ) \
                or ( prev and ( prev == curr.lchild or prev == curr.rchild ) ):
            print( curr.value )
            s.pop()
            prev = curr
        else:
            if curr.rchild: #先右节点先入栈，左节点后入栈，这样判断栈顶的时候总是左节点先出
                s.append( curr.rchild )
            if curr.lchild:
                s.append( curr.lchild )

方法二

def bin_tree_post_order_traverse1( root):
    '''
    利用两个栈实现
    '''
    s1 = []
    s2 = []
    s1.append( root )
    while s1:
        node = s1.pop()
        s2.append( node )
        if node.lchild:
            s1.append( node.lchild )
        if node.rchild:
            s1.append( node.rchild )
    while s2:
        print(s2.pop().value)

方法三

def bin_tree_post_order_traverse3(root):
    '''
    利用一个栈和两个标志节点实现后序遍历
    '''
    s=[]
    s.append(root)
    cur=None
    prev=root
    while s:
        cur=s[-1]
        # 当前节点的左节点存在，且它的左节点和右节点都没有打印过
        if cur.lchild and prev!=cur.lchild and prev!=cur.rchild:
            s.append(cur.lchild)
        elif cur.rchild and prev!=cur.rchild:
            # 运行到这里表明当前节点的左节点已经打印过了
            s.append(cur.rchild)
        else:
            print(s[-1].value)
            s.pop()
            prev=cur

广度优先遍历(层次遍历)

从树的root开始，从上到下从从左到右遍历整个树的节点

def breadth_travel(self, root):
            """利用队列实现树的层次遍历"""
            if root == None:
                return
            queue = []
            queue.append(root)
            while queue:
                node = queue.pop(0)
                print node.elem,
                if node.lchild != None:
                    queue.append(node.lchild)
                if node.rchild != None:
                    queue.append(node.rchild) 

求二叉树的深度

# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
    def maxdepth(self, root):
        if root is None:
            return 0
        return max(self.maxdepth(root.left), self.maxdepth(root.right))+1

 求二叉树的深度或者高度的非递归实现，本质上可以通过层次遍历实现，方法如下：

1. 如果树为空，返回0 。
2. 从根结点开始，将根结点拉入列。
3. 当列非空，记当前队列元素数（上一层节点数）。将上层节点依次出队，如果左右结点存在，依次入队。直至上层节点出队完成，深度加一。继续第三步，直至队列完全为空。

代码实现如下：

 def get_depth(self):
        """method of getting depth of BiTree"""
        if self.root is None:
            return 0
        else:
            node_queue = list()
            node_queue.append(self.root)
            depth = 0
            while len(node_queue):
                q_len = len(node_queue)
                while q_len:
                    q_node = node_queue.pop(0)
                    q_len = q_len - 1
                    if q_node.left is not None:
                        node_queue.append(q_node.left)
                    if q_node.right is not None:
                        node_queue.append(q_node.right)
                depth = depth + 1
            return depth

比较两棵树是否相同

# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
    def issame(self, root1, root2):
        if root1 is None and root2 is None:
            return True
        elif root1 and root2:
            return root1.val==root2.val and issame(root1.left, root2.left) and issame(root1.right, root2.right)
        else:
            return False

线索二叉树

加上结点前趋后继信息（结索）的二叉树称为线索二叉树。对于二叉树的线索化，实质上就是遍历一次二叉树，只是在遍历的过程中，检查当前结点左，右指针域是否为空，若为空，将它们改为指向前驱结点或后继结点的线索。前驱就是在这一点之前走过的点，不是下一将要去往的点。

线索化的实质就是将二叉链表中的空指针改为指向前驱或后继的线索。由于前驱和后继信息只有在遍历该二叉树时才能得到，所以，线索化的过程就是在遍历的过程中修改空指针的过程。

树和森林

将树转化成二叉树：右子树一定为空

1. 加线：在兄弟之间加一连线
2. 抹线：对每个结点，除了其左孩子外，去除其与其余孩子之间的关系
3. 旋转：以树的根结点为轴心，将整树顺时针转45°

森林转换成二叉树：

1. 将各棵树分别转换成二叉树
2. 将每棵树的根结点用线相连
3. 以第一棵树根结点为二叉树的根

树与转换后的二叉树的关系：转换后的二叉树的先序对应树的先序遍历；转换后的二叉树的中序对应树的后序遍历

哈夫曼树

哈夫曼树是一种带权路径长度最短的二叉树，也称为最优二叉树

构造方法见：https://www.cnblogs.com/mcgrady/p/3329825.html

一些概念

1. 路径：从一个祖先结点到子孙结点之间的分支构成这两个结点间的路径；
2. 路径长度：路径上的分支数目称为路径长度；
3. 树的路径长度：从根到每个结点的路径长度之和。
4. 结点的权：根据应用的需要可以给树的结点赋权值；
5. 结点的带权路径长度：从根到该结点的路径长度与该结点权的乘积；
6. 树的带权路径长度=树中所有叶子结点的带权路径之和；通常记作 WPL=∑wi×li
7. 哈夫曼树：假设有n个权值(w1, w2, … , wn)，构造有n个叶子结点的二叉树，每个叶子结点有一个 wi作为它的权值。则带权路径长度最小的二叉树称为哈夫曼树。最优二叉树。

给定n个权值作为n的叶子结点，构造一棵二叉树，若带权路径长度达到最小，称这样的二叉树为最优二叉树，也称为霍夫曼树(Huffman Tree)。霍夫曼树是带权路径长度最短的树，权值较大的结点离根较近。

假设哈夫曼树是二叉的话，则度为0的结点个数为N，度为2的结点个数为N-1，则结点总数为2N-1。哈夫曼树的结点个数必为奇数。

哈夫曼树不一定是完全二叉树，但一定是最优二叉树。

若度为m的哈夫曼树中,其叶结点个数为n,则非叶结点的个数为[(n-1)/(m-1)]。边的数目等于度。

哈夫曼编码

利用哈夫曼树求得的用于通信的二进制编码称为哈夫曼编码。树中从根到每个叶子节点都有一条路径，对路径上的各分支约定指向左子树的分支表示”0”码，指向右子树的分支表示“1”码，取每条路径上的“0”或“1”的序列作为各个叶子节点对应的字符编码，即是哈夫曼编码。

总节点数是叶子结点的2*n-1倍，而叶子结点就是我们的初始节点

class Node():
    def __init__(self,item):
        self.item=item
        self.isin=False
        self.left=None
        self.right=None

class HuffmanTree():
    def __init__(self,l):
        self.li=[]
        for x in range(0,len(l)):
            self.li.append(Node(l[x]))
        K=Node(float('inf'))
        while len(self.li)< 2*len(l)-1:
            m1=m2=K
            for x in range(0,len(self.li)):
                if m1.item>self.li[x].item and (self.li[x].isin is False):
                    m2=m1
                    m1=self.li[x]
                elif m2.item>self.li[x].item and (self.li[x].isin is False):
                    m2=self.li[x]
 
            H=Node(m1.item+m2.item)
            H.right=m1
            H.left=m2
            self.li.append(H)
            m1.isin=m2.isin=True
            print 'm1=%d m2=%d m1+m2=%d' % (m1.item,m2.item,H.item)