具体函数单调性&最值与求导的内在联系

具体函数单调性&最值与求导的内在联系

0.前言

遥记得一年多前的那个寒假，在JSOI冬令营有幸和GKdalao分到一个宿舍。那时他上高一，以下是当时他和同学间的一段对话——

​ -“GKdalao,这题咋做？” -“求导！”

​ -“呃，这题呢？” -“求导！”

​ -“……” -“不都说了吗，求导啊，什么题都可以求导啊！” （脑补一下对方自闭的眼神）

不仅如此，GKdalao还教了我们求导……不过，我当时就想问，求导有什么用吗？

几星期前，江巨佬路上随口pia了道物理题给我。不管三七二十一，随手直角分解一下，懵了，要求一个玩意的最值。一筹莫展之际，全校最帅最聪明最温柔的数学老师惊现宿舍门口，他看了眼式子，说到：“求导。”

我：……_{（想了一晚上木有睡着，不过第二天早上突然明白咋做了）}

从此以后，看到什么恒成立，最值，单调性，求导就完事了QωQ。_{（周围的人：闭嘴吧你整天求导求导……）}

1.导函数是个啥，能吃吗

其实，学到今天，导函数什么的，你其实已经初步了解了。

什么，你没学过？回想一下，下面这张图，是不是很眼熟？

那么，我就要问了，t1时刻的加速度有多大呢？

这不是弱智问题嘛。就是经过点(t1,v1)的图象切线的斜率大小。_{（如果你还不会的话，好好请教一下你的物理老师）}

那让我们继续。如果说，让我们把v和a分别看作是t的一个函数，即v=f(t)、a=g(t)，事实上，此时的g(t)就是f(t)的导函数。

哦，原来这就是导函数，是反映原函数的变化快慢的函数。

给出百度百科上的定义：

导数（Derivative），也叫导函数值。又名微商，是微积分中的重要基础概念。当函数y=f（x）的自变量x在一点x0上产生一个增量Δx时，函数输出值的增量Δy与自变量增量Δx的比值在Δx趋于0时的极限a如果存在，a即为在x0处的导数，记作f’（x0）或df（x0）/dx。

对于可导的函数f(x)，x↦f’(x)也是一个函数，称作f(x)的导函数（简称导数）。

嗯，就是酱=￣ω￣=（事实上看着定义一脸发懵）

---

2.How to 求导

先贴一下公式：

解释一下：

其中的f’(x)表示导函数，${\lim }_{\Delta x\to 0}$表示让$\Delta x$趋近于0。事实上，它就是求接近那一点上的斜率。

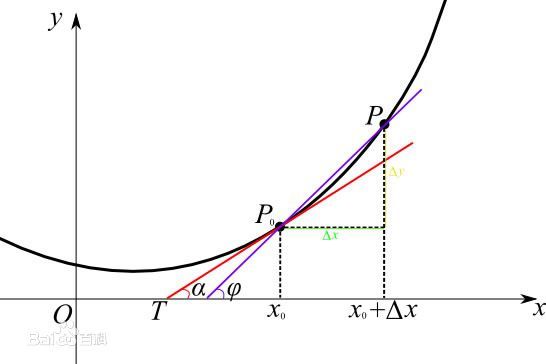
先取P点，让直线$P{P}_0$近似代表$P_0$处斜率。随着点$P$越来越靠近$P_0$点，直线$P{P}_0$也越来越趋近$P_0$处曲线的切线。易知，当$P$与$P_0$重合，即$\Delta x$=0时，直线$P{P}_0$即是$P_0$处曲线的切线，此时它的斜率即是点$P_0$处即x=$x_0$的导数。

说了这么多，原理是懂了，可是这个极限咋整呢？

其实木有关系，先带着极限算，算到不能再算以后，把$\Delta x$全变成0就OK了。

是不是很简单？

如果算起来还有什么困难的，请参照如下导数表和复合函数求导法则。

关于求导先讲到这里，感兴趣的童鞋自行百度（￣︶￣）↗

---

3.导函数又不能吃，有啥用呢

还记得本文开头所说的吗？

从此以后，看到什么恒成立，最值，单调性，求导就完事了。

Why?

再回想一下，做变加速直线运动的物理题的时候，当你发现加速度减小到0的时候，你就知道速度达到最值了。

再不行画张图分析一下，惊奇的发现，导函数大于0时，原函数单增，导函数小于0时，原函数单减。那么，导函数等于0呢？

这时候函数上升到了一个顶峰，我们称之为极值。通过比较极值和端点的大小，我们便能确定函数在给定区间内的最值。

让我们来分析一下这些问题的性质。事实上，无论是恒成立还是值域题，如果给我们最值，这些问题就根本不是问题。（废话）

那通过求导，我们有了什么？最值。

巧了，两者完美吻合。

这么一说，你应该能体悟到导函数在这点上的运用了吧。

于是，从此以后，看到什么恒成立，最值，单调性，求导就完事了。（小心被你的数学老师拍死）

---

4.既然我一样用不了导函数，学了有啥用

目前，我们只学了一种证明单调性的方法：定义法。

步骤就是先任取，再做差，最后定号。

留心生活的童鞋不难发现，定号的最简式子中往往甚至一定含有这个因式：$(x_2-x_1)$。

难道这仅仅是巧合吗？还是老师们所谓的经验之谈？

回归一下求导的过程，如果我们把$x$写作$x_1$，把$x+\Delta x$写作$x_2$，

先不考虑${\lim }_{\Delta x\to 0}$，事实上，我们直接将做差的结果除以了一个恒正的式子，再判断了剩余部分的正负。

如果不把$(x_2-x_1)$除了，仅将它提出来，判断整体的正负，又与求导有何异呢？

还有一点值得关注的是，由函数单调性引出的二元恒成立问题，在分区间时，往往把$x_1、x_2$看作是等价的，有什么依据吗？难道又是什么经验之谈？

事实上，如果我们把$x_1$写作$x$，把$x_2$写作$x+\Delta x$，再带上${\lim }_{\Delta x\to 0}$，此时$x_1、x_2$就相等了。

哦，原来大家所谓的经验之谈全是高等数学知识w(ﾟДﾟ)w

---

嗯，到这里本文就结束了。

如果对以上内容有什么问题的，欢迎评论。

以上内容皆是近期的一些小小思考 ，觉得憋在心里太难受了，就随手写下发出来。