多变量微积分（4）——多重积分之三重积分

本博客对应我博客中的 多变量微积分目录下的第四章，多重积分之三重积分。

最近选了数学物理方法这门课，不得不重新复习微积分，尤其是多元微积分。

4. 多重积分之三重积分

前一章的二重积分只是三重积分的一种简化。在物理学中用的最多的还是三重积分。这一章的思路是先介绍三种正交坐标系下的微分形式该如何表达，再介绍三维空间中的矢量场（其中包括三维空间下的旋度，散度，格林定理和stokes定理等），最后介绍麦克斯韦方程组。

4.1 三种正交坐标系下的三重积分

坐标系可以分为直角坐标系和曲线坐标系（典型的有柱坐标和球坐标），它们之间可以相互变换，可以参考我这篇博客《R3空间曲线坐标系变换及向量分析》

回归正题，三重积分的表达式是：
$${\iiint }_{R}fdV$$
公式中$dV$的表达方式可以有不同种选择。直角坐标系，柱坐标和球坐标系都是正交坐标系，即坐标系的三个基向量都是互相垂直的，直角坐标系最为特殊，它的三个维度方向是固定的；柱坐标系的z轴是固定的；而球坐标系的三个维度的方向都是随半径的变化而变化的。

4.1.1 直角坐标系下三重积分

直角坐标系下的三重积分形式如下：
$${\iiint }_{R}fdzdydx$$
上述公式可以算是通用的表达形式了，如果只是单纯求体积的话，令$f=1$，公式就变成了：
$$V=\iiint dV=\iiint dzdydx$$
（注意，以上只是表达形式，如果具体要求某个物体的体积或者通量之类的，需要选取积分上下限，这部分内容我放到了4.1.4）

其按z方向的投影是: $$dS=dxdy$$

4.1.2 柱坐标系下三重积分

柱坐标系是在极坐标的基础上加上了竖直方向的z轴。
其一般的三重积分形式就是：
$${\iiint }_{R}f\cdot dzrdrd\theta$$

只求体积的话就是：
$${\iiint }_{R}dzrdrd\theta$$
牢记极坐标与直角坐标系的转化：
$$\{\begin{array}{l}x=r\cos \theta \\ y=r\sin \theta \\ x^2+y^2=r^2\end{array}$$

按z轴进行投影的面积元公式为：
$$dS=rdrd\theta$$

4.1.3 球坐标系下三重积分

球坐标系是将直角坐标系的三个方向都换成了极坐标。
球坐标和柱坐标转换关系如下：
$$\{\begin{array}{l}z=\rho \cos \varphi \\ r=\rho \sin \varphi \end{array}$$
球坐标和直角坐标转换关系如下：
$$\{\begin{array}{l}x=\rho \sin \varphi \cos \theta \\ r=\rho \sin \varphi \sin \theta \\ z=\rho \cos \varphi \\ \rho =\sqrt{x^2+y^2+z^2}=\sqrt{r^2+z^2}\end{array}$$
球坐标下三重积分的形式：
$${\iiint }_{R}f\cdot {\rho }^2\sin \varphi d\rho d\varphi d\theta$$
其体积元的形式是：
$$dV={\rho }^2\sin \varphi d\rho d\varphi d\theta$$
其$\rho$方向上的面积元形式是：
$$dS=\underset{\text{height}}{\rho d\varphi }\cdot \underset{\text{length}}{\rho \sin \varphi d\theta }={\rho }^2\sin \varphi d\varphi d\theta$$

注意：

4.1.4 积分上下限的选择

以上的三节重点是关注三重积分的形式，如果要具体计算某个三重积分，需要我们谨慎地选择坐标系形式和积分的上下限。本节就以涉及直角坐标和柱坐标的例题来介绍如何选取上下限。
例题
求曲线$z=4-x^2-y^2$和$z=x^2+y^2$围成的立体区域的体积。

解题步骤：

1. 选取第一个投影方向，本题中选择竖直方向z方向进行投影，其积分上下限为：
   $x^2+y^2$和$4-x^2-y^2$

2. 画出两曲线相交的平面，并将其投影到x-y平面，本例中的相交平面是：
   $x^2+y^2=2$，是一个圆，如果选择直角坐标系会使问题变复杂。

3. 观察该平面的形状，选择相应的坐标系。（这里选取极坐标，整体来说就是柱坐标），其相应的坐标上下限是:
   $$V={\int }_0^{2\pi }{\int }_0^{\sqrt{2}}{\int }_{r^2}^{4-r^2}dzrdrd\theta$$

4.1.5 任意曲面的面积元

方法一

如果某个曲面的表达形式是$z=f(x,y)$，如果选择的是直角坐标系的话且投影到水平面的话，面积元$\mathbf{n}dS=\pm <-f_x,-f_y,1>dxdy$
证明过程：

假设任意两个不共线的向量$\mathbf{u},\mathbf{v}$，则它们就能够构成面积元：$\mathbf{n}\Delta S=\pm \mathbf{u}\times \mathbf{v}$
上述式子满足叉乘的基本性质，即叉乘的结果是有着面积元的大小$\Delta S$的法向量。如下图，假设$\mathbf{u}$的方向是沿着$x$的方向，$\mathbf{v}$的方向是沿着$y$的方向，那么：
$$\mathbf{u}=(x+\Delta x,y,f(x+\Delta x,y))-(x,y,f(x,y))$$
又因为：
$$f(x+\Delta x,y)\approx f(x,y)+f_x\Delta x$$
所以，
$$\mathbf{u}=(x+\Delta x,y,f(x,y)+f_x\Delta x)-(x,y,f(x,y))=<\Delta x,0,f_x\Delta =\Delta x<1,0,f_x>$$

同理，
$$\mathbf{v}=\Delta y<0,1,f_y>$$
两者的叉乘结果是：$\mathbf{u}\times \mathbf{v}=<-f_x,-f_y,1>\Delta x\Delta y$
也就得出:
$$\mathbf{n}d\sigma =<-f_x,f_y,1>dxdy$$

方法二

当某一曲线的表达式为：$f(x,y,z)=C$的时候，也就是曲线被表达成了等值面的时候可以用以下方法，因为梯度向量与等值面垂直，所以推导过程如下图：

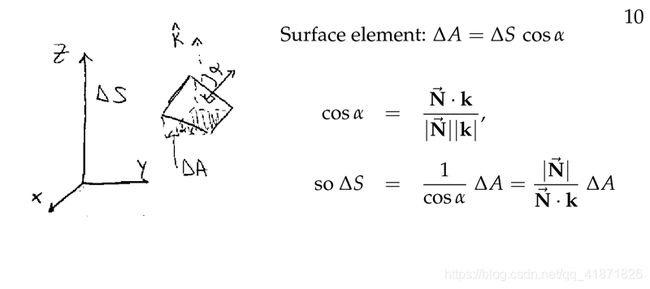
图中面积元$\Delta S$与它的投影$\Delta A$之间存在一个余弦值的关系。该余弦值可以通过两面积元的法向量的夹角计算得出，也就是$$d\sigma =\frac{\nabla f}{f_z}dA$$
其中，$\nabla f=<f_x,f_y,f_z>$

因为最近修的课程数学物理方法中涉及了正交曲线坐标系的变换方法，所以这一部分我会最近单独写一篇。

4.2 矢量场中的多重积分（重点）

4.2.1 三维矢量场

上一章中提到了平面内的向量场，这一章讲三维平面内的矢量场。
三维矢量场的形式如下：
$$\mathbf{F}(x,y,z)=M(x,y,z)\mathbf{i}+N(x,y,z)\mathbf{j}+P(x,y,z)\mathbf{k}$$
如果$,M_x,M_y,M_z,N_x,N_y,N_z,P_x,P_y,P_z$都存在并且是连续的，则$\mathbf{F}$就是连续可微的。

三维矢量场的实例:
场的本意就是尽管它与物体不接触，但它会对物体产生作用力。

1. 力场
   力场的例子可以是重力场，静电场，电磁场等。
2. 流体或速度场
   例如描述空间中流体的运动的速度场。

4.2.2 三维空间中的通量及环量

通量Flux

三维矢量场穿过一个平面S的通量是：
$$\text{Flux}={\iint }_S\mathbf{F}\cdot \mathbf{n}d\sigma$$
4.1.5中介绍了$\mathbf{n}d\sigma$的两种计算方法，这里假设我们使用第二种，上述公式就变成了：
$$\text{Flux}={\iint }_S\mathbf{F}\cdot \mathbf{n}d\sigma ={\iint }_S\mathbf{F}\cdot \frac{\nabla g}{|\nabla g_z|}dA$$

环量Circulation

三维矢量场流经一条闭合曲线C的环量是：
$$\text{Circulation}={\oint }_C\mathbf{F}\cdot d\mathbf{r}$$
这里环量的表达形式虽然和平面环量没有不同，但是维度已经变成了三维。

4.2.3 三维空间中的散度和旋度

散度

数学表达式
一个向量场$\mathbf{F}=M\mathbf{i}+N\mathbf{j}+P\mathbf{k}$的散度为：
$$\text{div}\mathbf{F}=\nabla \cdot \mathbf{F}=\frac{\partial M}{\partial x}+\frac{\partial M}{\partial y}+\frac{\partial P}{\partial z}$$

物理解释
散度描述的是单位体积内由源产生的通量。
比如电场的散度定义为：
$$\text{div}\mathbf{E}=\underset{\Delta V\to 0}{\lim }\frac{1}{\Delta V}\oint \mathbf{E}\cdot \mathbf{n}d\sigma$$

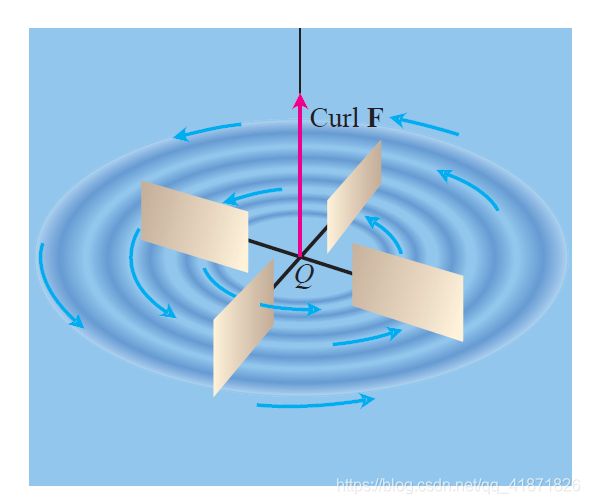
旋度

数学表达式
三维矢量场的旋度定义为：
$$\text{curl}\mathbf{F}=\nabla \times \mathbf{F}=\left|\begin{array}{ccc}\mathbf{i}& \mathbf{j}& \mathbf{k}\\ {\partial }_x& {\partial }_y& {\partial }_z\\ M& N& P\end{array}\right|$$
$$\text{curl}\mathbf{F}=\nabla \times \mathbf{F}=(P_y-N_z)\mathbf{i}+(M_z-P_x)\mathbf{j}+(N_x-M_y)\mathbf{k}$$
需要注意的是，二维平面中的旋度是三维旋度的$z$轴分量。

物理解释
旋度可以是速度场某个方向的角速度。

特殊情况
梯度的旋度为0:
$$\nabla \times \nabla f=0$$

4.2.4 三维空间中的散度定理和Stokes定理

A.散度定理 (Divergence Theorem)

三维向量场$\mathbf{F}$穿过一个闭合曲面$S$的通量（S的外法向量）等于散度在封闭曲面S包围下的体积D的积分，其数学表达为：
$$\iint \mathbf{F}\cdot \mathbf{n}d\sigma ={\iiint }_D\nabla \cdot \mathbf{F}dV$$

从量纲的角度理解这个公式我们可以发现，右边的$\nabla$算子对向量场$\mathbf{F}$进行了降维，但为了保证通量的量纲一致，右边方程必须要对封闭曲面S包围的体积D进行积分。这与散度的定义是一致的，散度是与面积无关的量。

B.Stokes定理

三维向量场$\mathbf{F}$流经一个闭合曲线$C$的环量等于旋度在曲面包围下的面积S的积分，其数学表达为：
$$\underset{CounterclockwiseRotation}{{\oint }_C\mathbf{F}\cdot d\mathbf{r}}={\iint }_S\nabla \times F\cdot \mathbf{n}d\sigma$$

4.3 三重积分的应用

三重积分的应用与二重积分的应用其实没有本质性的差别，重点还是在求三维物体的质量，质心，转动惯量等。

4.4 三重积分的实例——麦克斯韦方程组

麦克斯韦方程组是三重积分，通量环量和相关的散度定理stokes定理的一个非常重要的应用。我推荐以下三篇长尾科技的文章，尽管稍微有点长，但是写的非常通俗易懂，我觉得非常管用。我过几天再看一遍然后总结成单独的文章好了。
积分形式
微分形式
电磁波方程推导

参考

1. 《托马斯微积分》
2. 长尾科技公众号