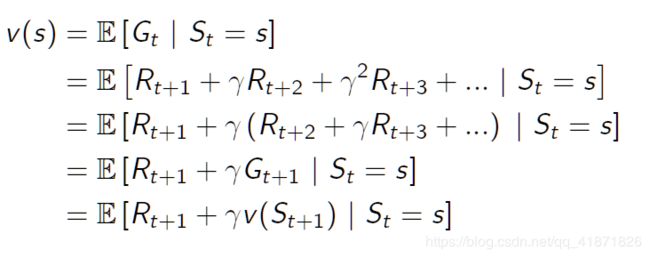强化学习笔记（2）——MDP

本文概要

本文个人是对david silver强化学习课程第二课的总结，有任何不足之处希望大家指正！

马尔可夫决策过程（MDP）精确描述了环境，MDP假设环境是完全可观的并且环境中所有的状态都满足马尔可夫性。本节课老师的讲解思路是先从最基本的马尔可夫开始，一步增加某些元素过渡到MDP的具体数学模型，最后提出求得最优解的方法。

1. 马尔可夫过程（Markov Process）

1.1 MP定义

（不知道为什么从思维导图复制过来的截图变色了…）
从中可以看出MP的组成为$<S,P>$,其中$P$是由状态转移概率$P_{s{s}^{\prime }}$（这里只描述了状态转移，没有涉及到后文的策略和动作）组成的状态转移矩阵，需要注意行列的顺序，从每一列第一个元素起始，到每一行的其他元素，如下图

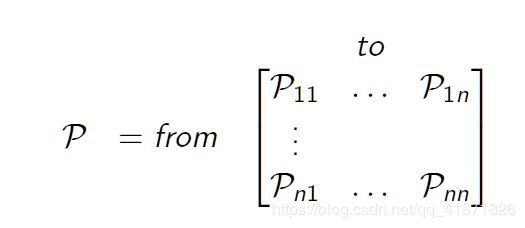
1.2 直观例子

本节课基本所有例子都在用学生上课过程的例子，如下图：

左图中圆圈代表状态，正方形代表停止的状态（实际过程中并不确定程序什么时候会停止）。右边是该过程的状态转移矩阵。假设我们从class 2状态开始进行采样，每一个时段内我们都会得到不同的状态序列，例如：
$$C2,C3,Pass,Sleep$$$$C2,C3,Pub,C2,Sleep$$$$C2,C3,Pub,C1,C2,Sleep$$$$C2,C3,Pub,C1,FB,FB,C1,C2,C3,Pass,Sleep$$

2. 马尔可夫收益过程（Markov Reward Process）

2.1 MRP定义

直观理解：MRP与MP类似，只是在MP的基础上加上了收益信号和折扣因子（discount factor），下图蓝色区域已经标出。

准确定义如下图：

定义中的收益函数$R$是收益（标量信号）的期望，为什么收益函数需要用期望来表示？（下文MRP与MDP的关系也会提到），原因在于智能体在某个状态下，在不同的采样时刻可能获得的收益都是不同的。我觉得可以用一个游戏的例子来理解这个概念，比如在王者荣耀对局中，比如说你选择的是中路法师，现在在中路清理兵线，在某一个时候只有你一个人在清理兵线，那么你会独享这些收益；但是下一时刻，可能队友在你身边，那么收益就会降低。

折扣因子
使用折扣因子的原因：

• 数学表达上的方便
• 避免无限返回值
• 并不会完全描述未来的不确定性

2.2 根据定义中的量描述长期收益

返回值（Returns）

返回值（这里直接翻译了，也有更好的翻译是“回报值”）的定义如下所示：

这里折使用扣系数的幂次与未来的收益相乘，表达的物理意义就是在当前时刻下智能体对未来收益的一种"估算"。

值函数（Value Function）

在第一节课的笔记中提到，引入值函数的目的就是用来描述状态的长期收益或价值。准确定义如下：

2.3 MRP的贝尔曼方程（Bellman Equation）

数学推导过程及表达形式

贝尔曼方程的目的：

贝尔曼方程的目的就是将上文中的值函数分解成两个部分：第一是当前立即获得的收益（immediate reward）；第二个是下一个状态值函数的折扣值（discounted value）

这里把结论再重复一下（重要结论，下文推导也要使用）：
$$v(s)=\mathbb{E}[R_{t+1}+\gamma v(S_{t+1}=s^{\prime })|S_t=s]$$

贝尔曼方程的进一步化简

根据以上的结论，可以看出值函数的定义和贝尔曼方程中涉及到了期望函数，所以我们可以利用期望的线性叠加性质对公式进行化简（为了表示方便，把$v(S_{t+1}=s^{\prime })$表示成$v(s^{\prime })$）：
$$v(s)=\mathbb{E}[R_{t+1}+\gamma v(s^{\prime })|S_t=s]=\mathbb{E}[R_{t+1}]+\gamma \mathbb{E}[v(S_{t+1}=s^{\prime }|S_t=s)]$$$$=R_{t+1}+\gamma \sum _{s^{\prime }\in S}v(s^{\prime })\mathbb{P}[S_{t+1}=s^{\prime }|S_t=s]$$从而可以得到：$$v(s)=R_{t+1}+\gamma \sum _{s^{\prime }\in S}v(s^{\prime })P_{s{s}^{\prime }}$$

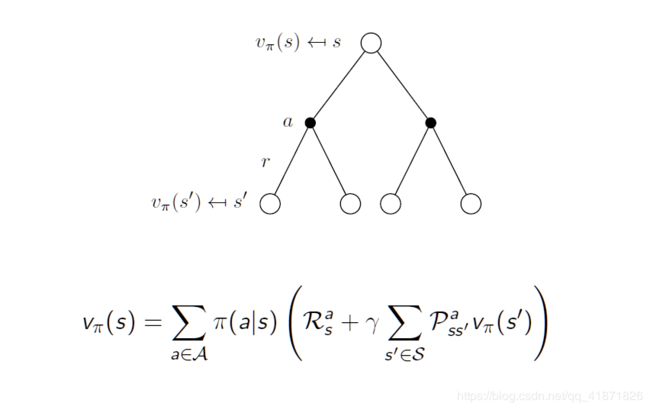
用以下的树状图可以解释以上公式：

一个计算MRP中值函数的例子($\gamma =1$)：
除了下图中给出的状态，也可以计算其他状态的值。例如，左上角的状态值：$-23=-1+-23\times 0.9+(-13\times 0.1)$
这里$-1$代表到达左上角状态之后有的收益，也就是上述方程中的，后面是从当前状态可能到达的状态值乘以对应的状态转移概率。

贝尔曼方程的矩阵形式及解法

在上文化简的基础上，将以上公式写称矩阵形式：
$$\left[\begin{array}{c}v(1)\\ ⋮\\ v(n)\end{array}\right]=\left[\begin{array}{c}{R}_1\\ ⋮\\ R_n\end{array}\right]+\gamma \left[\begin{array}{ccc}{P}_{11}& \dots & P_{1n}\\ ⋮& & \\ P_{n1}& \dots & P_{nn}\end{array}\right]\left[\begin{array}{c}v(1)\\ ⋮\\ v(n)\end{array}\right]$$

以上矩阵形式也可以直接用以下方程来表示$$\text{v}=\text{R}+\gamma P\text{v}$$
（加粗的字母代表向量，$P$表示状态转移矩阵）

a. 直接求解法
由线性代数的一些基本概念可以知道，以上方程可以通过矩阵求逆来求解：
$$\text{v}=(I-\gamma P{)}^{-1}\text{R}$$

存在的问题：

1. 算法复杂度为$O(n^3)$
2. 只适用于小数据量的MRP

b. 迭代法求解法（该系列后面的课程应该都会涉及到）

1. 动态规划
2. 蒙特卡洛方法
3. 时序差分法

3. 马尔可夫决策过程（Markov Decision Process）

3.1 MDP定义

有了前文的MP和MRP，在此基础上加上“决策”相关的定义就构成了MDP。准确定义如下图：

与MRP对比可以发现，收益函数、状态转移概率的定义都多了一个动作的先验条件。而动作的概率分布就是策略。

需要说明的是，课程里的状态转移概率和矩阵其实做了省略，MDP中所谓的状态转移其实是后继状态和后继状态带来的收益的联合概率分布，即$p(s^{\prime },r|s,a)=\mathbb{P}[S_{t+1}=s^{\prime },R_{t+1}=r|S_t=s,A_t=a]$，这里的状态转移概率$P_{s{s}^{\prime }}^a=\sum _{r}p(s^{\prime },r|s,a)$得到的边缘概率分布。

3.2 策略

策略的定义

1. 随即策略（策略是动作的概率分布）
   
2. 确定性策略：$a=\pi (s)$

策略的特点

1. 策略完整定义了智能体的行为
2. MDP中的策略取决于当前状态（而不是历史）
3. 策略是静态stationary的，与时间无关，只与当前所处的状态有关。

3.3 MDP与MP、MRP的关系

根据MDP的定义，就可以发现其与MP、MRP的基本关系。

假设给定MDP和一个策略（即动作的概率分布已知），则状态序列$S1,S2,\dots$是一个MP，$<S,P^{\pi }>$（给先前MP定义中的P加上上标$\pi$）；如果在MP的基础上加上收益序列，则$S1,R1,S2,R2,\dots$构成MRP。

MRP与MDP中状态转移概率的关系
$$P_{s{s}^{\prime }}^{\pi }=\sum _{a\in \mathcal{A}}\pi (a|s)P_{s{s}^{\prime }}^a$$
该公式的推导来自于全概率公式，先回顾状态转移概率的准确定义：
$$P_{s{s}^{\prime }}^{\pi }=\mathbb{P}[S_{t+1}=s^{\prime }|S_t=s]$$而$$P_{s{s}^{\prime }}^a=\mathbb{P}[S_{t+1}=s^{\prime }|S_t=s,A_t=a]$$可以看出$P_{s{s}^{\prime }}^a$是基于$P_{s{s}^{\prime }}^{\pi }$的条件概率。又因为动作的概率分布已知，那么根据全概率公式就可以得到$$P_{s{s}^{\prime }}^{\pi }=\sum _{a\in \mathcal{A}}\pi (a|s)P_{s{s}^{\prime }}^a$$

MRP与MDP中收益信号的关系
同理，收益函数的关系也是类似的。
$$R_s^{\pi }=\mathbb{E}[R_{t+1}|S_t=s]$$而$$R_{s{s}^{\prime }}^a=\mathbb{E}[R_{t+1}|S_t=s,A_t=a]$$与之前唯一的区别就是定义中是期望函数，根据全概率公式也可以得到$$R_s^{\pi }=\sum _{a\in \mathcal{A}}\pi (a|s)R_s^a$$

3.4 MDP中的值函数定义

状态值函数

动作值函数

状态值函数的物理意义是衡量当前状态的好坏，而动作值函数的物理意义就是衡量执行当前动作的好坏。

这里$G_t$ 依然是返回值，之前的定义一样。

3.5 贝尔曼期望方程（Bellman Expectation Equation）

值函数分解

状态值函数分解

与MRP一样，状态值函数可以分解为当前收益和继任状态值的折扣值。
$$v_{\pi }(s)=\mathbb{E}[R_{t+1}+\gamma v_{\pi }(S_{t+1})|S_t=s]$$

动作值函数分解

动作值函数可以分解为当前收益和继任动作值的折扣值。
$$q_{\pi }(s,a)=\mathbb{E}[R_{t+1}+\gamma R_{t+2}+{\gamma }^2{R}_{t+3}+\cdots +{\gamma }^k{R}_{t+k+1}+\dots )|S_t=s,A_t=a]$$或者是

$$q_{\pi }(s,a)=\mathbb{E}[R_{t+1}+\gamma q_{\pi }(S_{t+1},A_{t+1})|S_t=s,A_t=a]$$

值函数迭代（或状态值与动作值的关系）

一步迭代回溯

1. 状态值函数

从上文的状态值函数和动作值函数的定义可以看出，这一步的推导依然是基于全概率公式。

2. 动作函数

这一步的推导基于动作值函数的定义：
$$q_{\pi }(s,a)=\mathbb{E}[G_t|S_t=s,A_t=s],G_t=R_{t+1}+\gamma v_{\pi }(S_{t+1}=s^{\prime })$$
联立两者可以得到：
$$q_{\pi }(s,a)=R_{t+1}+\gamma \mathbb{E}[v_{\pi }(s)|S_t=s,A_t=a]=R_{t+1}+\gamma \sum _{s^{\prime }\in \mathcal{S}}{v}_{\pi }(s)\mathbb{P}[S_t=s^{\prime }|S_t=s,A_t=a]$$$$=R_{t+1}+\gamma \sum _{s^{\prime }\in \mathcal{S}}{v}_{\pi }(s)P_{s{s}^{\prime }}^a$$
（推导思路就是将定义式在满足期望性质的前提下展开，其中$R_{t+1}$是确定的，可以提出来，后面的线性项根据返回值与状态值的关系继续化简）

两步迭代回溯

迭代两步的情况就是组合上文迭代一步的情况，第一种情况将动作值函数的表达形式带入状态值函数；第二种情况将状态值函数的表达式代入动作值函数。

1. 状态值函数

2. 动作值函数

贝尔曼方程的矩阵形式

贝尔曼方程的矩阵形式与MRP中的形式一样。

状态值函数的计算实例

图中的计算例子基于以下式子：

除了图中标出的状态，我们也可以看其他状态的值是怎么计算的，例如计算最中间的状态（值为2.7的状态）：$2.7=0.5\ast (-2+7.4)+0.5\ast 0$

4. 如何求得最优解

4.1 最优值函数 (Optimal Value Function) 定义

最优值函数的意义在于从所有策略中找到能够实现最大的状态值或者动作值的策略。MDP的解决过程就是求最优值函数找到最优策略的过程。

4.2 最优策略 (Optimal Policy)

最优策略的定义基于偏序关系，策略之间的比较基于该策略下所达状态值函数的大小。

上述定理说明：

1. 任意的MDP都存在至少一个最优策略。
2. 所有的最优策略都能让状态值函数、动作值函数达到最优。

4.3 如何寻找最优策略

方法：通过最大化动作值函数来寻找最优策略。

这里的最优策略的意义就是只使用能够让动作值函数最大的动作，也就是从原先的随机策略转化为了确定策略。

对上图的解释可以参考下表：

Action	Probability
$\underset{a\in \mathcal{A}}{\mathrm{argmax}}{q}_{\ast }(s,a)$	1
other actions	0

下图给出寻找最优策略的例子。比如起始点为左上角的点，如果已知了每一步中的$q_{\ast }(s,a)$，则最优策略会立即得到。

4.4 贝尔曼最优方程（Bellman Optimality Equation）

与贝尔曼期望方程的关系：
贝尔曼最优方程是建立在贝尔曼期望方程的基础上的，在假设得到最优策略的情况下对两种值函数做了更进一步的推断。

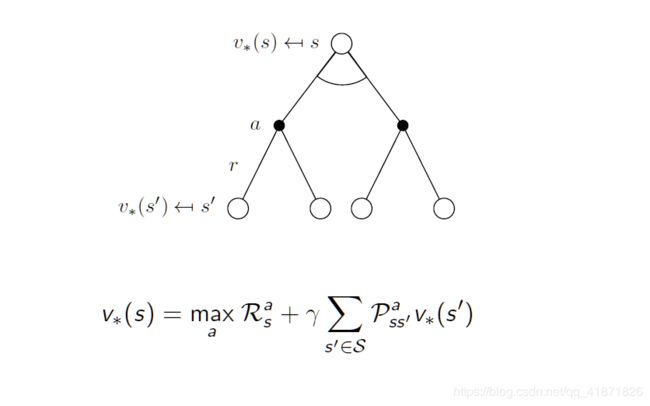
一步迭代回溯

1. 最优状态值函数
与前文的迭代方法几乎类似，唯一不同的就是最优的状态值是通过最大化最优动作值函数得到的，后文给出对于该公式的证明。

该关系可以通过反证法来证明：
首先最优策略本身也满足先前的贝尔曼期望方程，所以下式是一定成立的。但是这里只能说明是小于等于关系，而上图中的公式中只有等于，那么证明思路就就是用反证法说明该公式中不可能出现小于号。
$$v_{{\pi }_{\ast }}(s)=\sum _{a\in \mathcal{A}}{\pi }_{\ast }(a|s)q_{{\pi }_{\ast }}(s,a)\le \underset{a}{\max }{q}_{{\pi }_{\ast }}(s,a)$$
反证法：（参考《白板推导——强化学习系列》）
假设$v_{{\pi }_{\ast }}(s)<\underset{a}{\max }{q}_{{\pi }_{\ast }}(s,a)$，则可以构造一个新的策略${\pi }_{optional}(a|s)$，使其动作的概率分布满足下表：

${\pi }_{optional}$中的动作	probability
$\underset{a}{\mathrm{argmax}}{q}_{{\pi }_{\ast }}(s,a)$	1
other actions	0

这时利用上表的概率分布可得，$v_{{\pi }_{optional}}(s)=\sum _{a\in \mathcal{A}}{\pi }_{optional}(a|s)q_{{\pi }_{optional}}(s,a)=\underset{a}{\max }{q}_{{\pi }_{\ast }}(s,a)>v_{{\pi }_{\ast }}(s)$，又因为如果$v_{{\pi }_{optional}}(s)>v_{{\pi }_{\ast }}(s)$，则${\pi }_{optional}>{\pi }_{\ast }$，这与${\pi }_{\ast }$是最优策略相矛盾，所以一定存在：$$v_{{\pi }_{\ast }}(s)=\underset{a}{\max }{q}_{{\pi }_{\ast }}(s,a)$$

2. 最优动作值函数
最优动作值函数与之前的动作值函数迭代过程类似，只是将策略换成了最优策略${\pi }_{\ast }$，相应值函数也就换成了$v_{\ast }(s)$。

两步迭代回溯

1. 最优状态值函数
联立一步迭代回溯的情况，将最优动作值函数的表达式代入最优状态值函数。

2. 动作值函数
联立一步迭代回溯的情况，将最优状态值函数的表达式代入最优动作值函数。

5. MDP的扩展

1. Infinite and continuous MDP
2. Partially Observable MDP (POMDP)
3. Undiscounted, average reward MDPs