从KMP到FSA有限状态自动机字符串匹配

前言

在数据结构课上，老师先讲了Finite State Automata,说理解了FSA然后理解KMP就不难了，然而FSA一直没能讲明白怎么构造FSA来实现字符串匹配。而今天看了Analysis Of Algorithm之后才发现虽然KMP算法确实是相当于简化的FSA，但是用FSA来查找子串简直是杀鸡用牛刀（比如说FSA可以用来判断母串里是不是有偶数个a并且有奇数个b，etc…但是KMP就不行了）。
如果不明白FSA，推荐看这个博客以及上面提到的Analysis Of Algorithm.
如果不明白KMP，推荐看这个博客，写得非常好。

基本的FSA概念

在说KMP与FSA的关系之前，一些FSA里面的概念要了解一下。

1. 字符集∑ ，比如说∑={a,b,c}说明主串和子串中只含有a,b,c三个字母
2. 状态的有限集合Q， 用于字符串匹配时就是Q={1…m}，m是子串长度，状态1是初始态

当然算法导论里还有更多的相关概念，但是关于KMP的FSA用这两个就够了。
FSA里字符集∑的元素构成状态表的列，Q的元素（即每个状态）构成状态表的行。所以如果∑的大小为n, Q的大小是m，则表的大小是n*m，如果没有优化，中文的FSA状态表可以有20k列（所以说是杀鸡用牛刀)

KMP与FSA的关系

KMP是如何简化FSA状态表的？

FSA状态表里对∑的每个元素对应的每个状态都有记录，即一个元素一列。但是KMP的next数组是一维的，这是因为next数组只记录字串substr[i]处的状态转移，就是如果母串的字符和substr[i]不相等（不管是∑中哪一个元素），简化自动机应该跳转到哪个状态，这个就是next[i]记录的。

那next[]里是怎么记录状态集合Q的？是通过next[]的下标，也就是{0…(m-1)}，跟FSA的状态集合Q是一样的。但是默认的next[0] = -1，使得KMP的状态集合多出一个 -1，这个是由于要用来表明KMP里的简化自动机不接受的情形的（也就是母串不含模式串）。

简而言之，FSA状态表里存了Q中每个状态对应∑里每个元素的状态转移，而next[]只存了状态表的一部分信息，存着Q中每个状态对应遇到不匹配元素时的状态转移。很显然，next[]里的信息只是状态表的信息的一个很小的子集，但是这个子集足以用于字符串匹配了。而FSA状态表里多出来的信息使得FSA可以有更多的应用。

如何从next[]得到FSA的完整状态转移图？

用KMP，得出next[]，如果知道输入字符集∑，是可以得出完整的状态转移图的，当然也可以得出状态转移表。

举个例子，
令∑ = {a,b,c}
子串（模式串）为"ababc"
则Q为{0，1，2，3，4} （next[]的下标范围）
而举例子的时候我想在Q中加多一个元素，让Q = {0，1，2，3，4，5}，后面解释

用KMP算法算出next[]
再看这个博客
里面有优化了的next[]，也有没有优化的
优化的next[] 是 [-1, 0, -1, 0, 2]
没有优化的next[] 是 [-1, 0, 0, 1, 2]
而这两个next[]得出的FSA转移图是一样的（也证明了两个next[]是等价的）

首先我们可以很快画出以下

圆圈里正好是Q中元素，也表明了之前输入了多少个可接受的字符，比如①即前面输入了1个可接受的字符。到状态⑤，已经输入了5个可接受的字符，也就是ababc，就输出accepted.（这也是为什么我想加多一个状态5的原因）

然后从左往右建图：
首先是状态0，next[0] = -1,当输入为b,c时，不符合，所以跳转状态-1,这里我们令它跳转为状态0，因为输入了0个可接受的字符。
然后是状态1，next[1] =0，当输入a,c时，不符合，所以跳转状态0，我们先把箭头指向状态0，得到

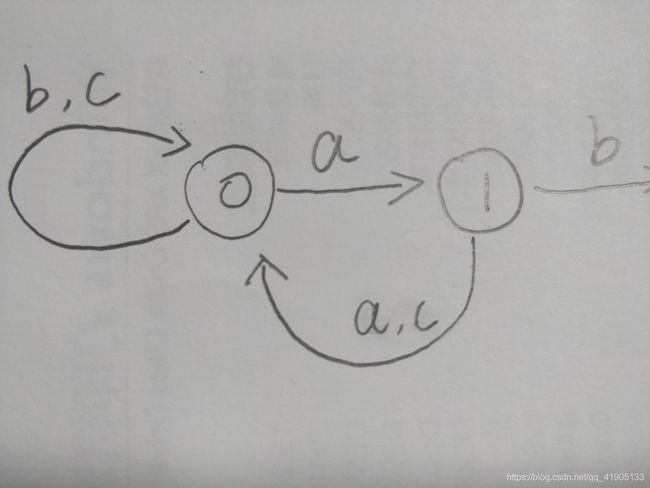
但是这个逻辑上有问题，因为next[]只说了不符合的时候跳转的状态，没有说输入a或者c时候跳转的状态。
所以这时候我们利用状态0的状态转移，状态0画出了当输入a时跳转到状态1，输入c时跳转状态0，所以我们得出状态1时如果输入a，不符合，应该跳转状态0，然后因为输入了a，之后应该跳转状态1，得出

这个才是正确状态转移图的一部分。
依此类推，在第n个状态，我们可以从next[]获得不符合时应该跳转的状态，然后我们跳转到状态next[n]，第next[n]个状态我们已经画好了状态转移，然后再根据不符合的输入各自根据第next[n]的状态转移图跳转到下一个状态。所以总共会跳转两次，第二次跳转到的状态就是我们要的。
最后，我们可以画出完整的FSA状态转移图了

画得丑别介意

这样子我们就有方法从next[]推出FSA状态转移表了，也有可能从FSA状态转移表推出next[]

但是互推好像并没有什么用处

更加重要的是这可以从KMP的角度理解怎么构造FSA去进行字符串匹配的
也就是在这个博客里面说到的：
一次读入T的一个字符，用S表示当前读入的T的字符，一开始读入一个字符，于是S=a.然后看看，从P开始，连续几个字符所构成的字符串可以成为S的后缀，由于当前S只有一个字符a,于是从P开始，连续1个字符所形成的字符串”a”,可以作为S的后缀。把这个字符串的长度记为k,于是此时k 等于1. 继续从T中读入字符，于是S=”ab”, 此时，从P开始，连续两个字符所构成的字符串”ab”可以作为S的后缀，于是k = 2.反复这么操作

为什么要这么操作？
回想KMP的next[]里面每一个元素表示的是字符串的前缀集合与后缀集合的交集中最长元素的长度，比如说"ababc"的未优化next[] = [-1, 0, 0, 1, 2], next[4]代表的是"ababc"中的’b’， 'b’之前的串是"aba"，字符串的前缀集合与后缀集合的交集中最长元素的长度为1.

中途插一句：
不过按照上面的说法，为什么next[0] = -1? 而之前从next[]构造FSA转移图时为什么把转移到-1状态直接归为转移到0状态呢？
直接从上面提到的KMP博客截图

所以对于"ababc"来说，更加原始的next[]应该是[0,0,0,1,2]，令next[0] = -1只是一个flag，用来指示应该是母串指针往后移一位了。

回到正题
刚好FSA字符串匹配里有S的后缀和P的前缀
再结合从next[]得到FSA的完整状态转移图的方法，好像我们可以发现其中的关联

直接引用一位大佬（Jerry Lu）的话

再次解读一下next[]，
比如说"ababc"的最原始next[]是[0,0,0,1,2]，next[3] =1，表明’b’位不匹配时跳到index =1位置，也就是说明要跳过1个字母（这一个字母已经匹配了），而构造的FSA里首先要跳到状态1，然后根据状态1的跳转图和这个不匹配的字母到底是什么决定第二次跳转要跳转到什么地方（参考建跳转图的步骤）。

上图相当于我们已经知道了#和%处字母不匹配，但是加上了#之后会不会有更短的匹配我们不知道，也就是下图的状况

所以我们从next[]建跳转图的时候需要二次跳转

而直接FSA建立跳转图的时候，则是一步到位，直接分析，s的后缀和p的前缀的最大符合的长度，也就是不符合时针对特定不符合输入需要跳转的不同状态（which also means 可以跳过多少个字符）

以上就是FSA字符匹配机和KMP的关系了，最关键的就是对next[]的解读而已。

最后感谢各位大佬的Carry