蓝桥杯练习系统-基础练习
题库截止至 2020-7-28
早就做完了,重新做一遍水下题,做到哪发到哪。
BASIC-1 闰年判断
问题描述
给定一个年份,判断这一年是不是闰年。
当以下情况之一满足时,这一年是闰年:
1. 年份是4的倍数而不是100的倍数;
2. 年份是400的倍数。
其他的年份都不是闰年。
输入格式
输入包含一个整数y,表示当前的年份。
输出格式
输出一行,如果给定的年份是闰年,则输出yes,否则输出no。
测试样例1
输入:
2013
输出:
no
测试样例2
输入:
2016
输出:
yes
数据规模与约定
1990 <= y <= 2050
这么把题摆出来还是比较无聊的,但是我闲啊。
比较人性的写法:
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int y = sc.nextInt();
if ((y & 1) == 0 && y % 4 == 0 && (y % 100 != 0 || y % 400 == 0)) System.out.println("yes");
else System.out.println("no");
}
}
利用短路逻辑运算符的特性,将判断条件依序排列,并且加上了奇偶校验优先排除奇数输入。
符合规模与约定的修改:
题目数据限制中,会出现能被100整除的数只有2000,而它同时又能被400整除。
换言之,在这个区间内能被4整除即是闰年,可以针对此项进行优化。
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int y = sc.nextInt();
if ((y & 1) == 0 && y % 4 == 0) System.out.println("yes");
else System.out.println("no");
}
}
甚者:
Scanner sc = new Scanner(System.in);
if (sc.nextInt() % 4 == 0) System.out.println("yes");
else System.out.println("no");
可以看到这种处理方式非常的不人性,因此不建议做题时往这种方向上看齐。
BASIC-2 01字串
问题描述
对于长度为5位的一个01串,每一位都可能是0或1,一共有32种可能。它们的前几个是:
00000
00001
00010
00011
00100
请按从小到大的顺序输出这32种01串。
输入格式
本试题没有输入。
输出格式
输出32行,按从小到大的顺序每行一个长度为5的01串。
测试样例
输出:
00000
00001
00010
00011
<以下部分省略>
比较人性(大概)的写法:
public class Main {
public static void main(String[] args) {
char[] blanc = {'0', '0', '0', '0', '0'};
for (int i = 0, n = 0, index = 4; i < 0x20; n = ++i, index = 4) {
do blanc[index--] = (char)(n & 1 | 0x30);
while ((n >>>= 1) != 0);
System.out.println(blanc);
}
}
}
这是我最开始写的思路(指一年前)
如果是C的话声明数组 char *blanc = “00000” 爽的爆批碎碎念
后来发现的 比较可沿用的思路:
public class Main {
public static void main(String[] args) {
for (int i = 0; i < 0x20; i++) {
for (int j = 4; j >= 0; j--) System.out.print(i >> j & 1);
System.out.print('\n');
}
}
}
如果是Pythond的话直接 else: print(’\n’) 同样爽的爆批碎碎念
当然Java也有Java的优势:
public class Main {
public static void main(String[] args) {
for (int i = 0; i < 0x20; i++) System.out.printf("%05d%n", Integer.parseInt(Integer.toBinaryString(i)));
}
}
若是能熟练掌握Java的API还相当强大的,但这种思路谈论性能还是得往后稍稍。
再者便是暴力解题:
for (int i = 0; i < 2; i++)
for (int j = 0; j < 2; j++)
for (int l = 0; l < 2; l++)
for (int x = 0; x < 2; x++)
for (int y = 0; y < 2; y++) System.out.println(i + "" + j + "" + l + "" + x + "" + y);
掌握暴力解题也是相当重要的一门功课,毕竟和一个精妙的思路相比,切实的结果我想更具有说服力。
暴力解题的方法有很多,网上也很容易找到,后面我便不收录了。
BASIC-3 字母图形
问题描述
利用字母可以组成一些美丽的图形,下面给出了一个例子:
ABCDEFG
BABCDEF
CBABCDE
DCBABCD
EDCBABC
这是一个5行7列的图形,请找出这个图形的规律,并输出一个n行m列的图形。
输入格式
输入一行,包含两个整数n和m,分别表示你要输出的图形的行数的列数。
输出格式
输出n行,每个m个字符,为你的图形。
测试样例
输入:
5 7
输出:
ABCDEFG
BABCDEF
CBABCDE
DCBABCD
EDCBABC
数据规模与约定
1 <= n, m <= 26
源码:
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt(), m = sc.nextInt();
StringBuilder line = new StringBuilder();
for (char i = (char)(n + 64); i > 'A'; i--) line.append(i);
for (char i = 'A', l = (char)(m + 'A'); i < l; i++) line.append(i);
while (n-- > 0) System.out.println(line.substring(n, n + m));
}
}
老实说最开始我并没有发现规律,当然这种说法是不严谨的,
但如若是编程或是数学谈论起规律,那指代的想必是一个通项公式。
换做是程序的话:
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt(), m = sc.nextInt();
StringBuilder out = new StringBuilder();
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) out.append((char)('A' + Math.abs(j - i)));
out.append('\n');
}
System.out.println(out);
}
}
这里我就不误人子弟了,我只是一个中职毕业大专在读的懒狗。
BASIC-4 数列特征
问题描述
给出n个数,找出这n个数的最大值,最小值,和。
输入格式
第一行为整数n,表示数的个数。
第二行有n个数,为给定的n个数,每个数的绝对值都小于10000。
输出格式
输出三行,每行一个整数。第一行表示这些数中的最大值,第二行表示这些数中的最小值,第三行表示这些数的和。
测试样例
输入:
5
1 3 -2 4 5
输出:
5
-2
11
数据规模与约定
1 <= n <= 10000
主观上感觉没有操作空间,就逼逼这么多。
源码:
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt(), max, min, temp, sum;
sum = max = min = sc.nextInt();
while (n-- > 1) {
sum += temp = sc.nextInt();
if (temp > max) max = temp;
else if (temp < min) min = temp;
}
System.out.print(max + "\n" + min + "\n" + sum);
}
}
BASIC-5 查找整数
问题描述
给出一个包含n个整数的数列,问整数a在数列中的第一次出现是第几个。
输入格式
第一行包含一个整数n。
第二行包含n个非负整数,为给定的数列,数列中的每个数都不大于10000。
第三行包含一个整数a,为待查找的数。
输出格式
如果a在数列中出现了,输出它第一次出现的位置(位置从1开始编号),否则输出-1。
测试样例
输入:
6
1 9 4 8 3 9
9
输出:
2
数据规模与约定
1 <= n <= 1000
同样的感觉没啥操作空间
线性查找:
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt(), a, i = 0, j = 0;
int[] arrays = new int[n + 1];
while (i < n) arrays[i++] = sc.nextInt();
a = arrays[n] = sc.nextInt();
while (arrays[j++] != a);
if (j <= n) System.out.println(j);
else System.out.println(-1);
}
}
这里进行了一点小优化,详见:link
但如果这道题增加了需求(当查找目标个数大于1时),折损一点空间可以换来不变的时间复杂程度。
毕竟这里规定了n为小于等于10000的自然数,也不算折损多少。
像是这样:
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt(), a, i = 0;
int[] arrays = new int[10000];
while (i++ < n) if (arrays[(a = sc.nextInt())] == 0) arrays[a] = i;
while (true) if (arrays[(a = sc.nextInt())] != 0) System.out.println(arrays[a]);
else System.out.println(-1);
}
}
但其实在Java来说、就该题而言,两者差距不大,长10000的数组看起来挺大,实际上也就莫约占用0.04M字节。
懒狗可以这样写(比如我):
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt(), i = 0;
int[] arrays = new int[n];
while (i < n) arrays[i++] = sc.nextInt();
if ((i = new String(arrays, 0, n).indexOf(sc.nextInt())) == -1) System.out.println(i);
else System.out.println(i + 1);
}
}
BASIC-6 杨辉三角形
问题描述
杨辉三角形又称Pascal三角形,它的第i+1行是(a+b)i的展开式的系数。
它的一个重要性质是:三角形中的每个数字等于它两肩上的数字相加。
下面给出了杨辉三角形的前4行:
1
1 1
1 2 1
1 3 3 1
给出n,输出它的前n行。
输入格式
输入包含一个数n。
输出格式
输出杨辉三角形的前n行。每一行从这一行的第一个数开始依次输出,中间使用一个空格分隔。请不要在前面输出多余的空格。
测试样例
输入:
4
输出:
1
1 1
1 2 1
1 3 3 1
数据规模与约定
1 <= n <= 34
源码:
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int[][] trian = new int[n][n];
for (int i = 0; i < n; i++) trian[i][0] = trian[i][i] = 1;
for (int i = 2; i < n; i++)
for (int j = i / 2; j > 0; j--)
trian[i][j] = trian[i][i - j] = trian[i - 1][j - 1] + trian[i - 1][i - j - 1];
for (int i = 0; i < n; i++) {
for (int j = 0; j <= i; j++) System.out.print(trian[i][j] + " ");
System.out.print('\n');
}
}
}
正儿八经的生成,正儿八经的输出 . . .
所以也就算的上通俗易懂,当然这里还有很大的优化空间。
初版优化:
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int[][] trian = new int[n][];
for (int i = 0; i < n; i++){
trian[i] = new int[i + 1];
trian[i][0] = trian[i][i] = 1;
for (int j = i / 2; j > 0; j--) trian[i][j] = trian[i][i - j] = trian[i - 1][j - 1] + trian[i - 1][i - j - 1];
}
for (int i = 0; i < n; i++) {
for (int j = 0; j <= i; j++) System.out.print(trian[i][j] + " ");
System.out.print('\n');
}
}
}
都是几个简浅的点,这里就不多说了
其实真硬要扣内存,只需两个长度为 n 的数组就完事了
除了根据两肩数字相加生成杨辉三角外,还有其他方法可以实现。
比如在百度百科里对性质的阐述:截止至2020-07-29
性质5:第n行的m个数可表示为 C(n-1,m-1),. . .
组合数计算公式:C(n, m) = n! / {m!(n - m)!}
表现在程序里:
注:该实现不可取
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
for (int i = 0; i < n; i++) {
for (int j = 0; j <= i; j++) System.out.print(factorial(i) / (factorial(j) * factorial(i - j)) + " ");
System.out.print('\n');
}
}
static int factorial(int n) {
if (n <= 1) return 1;
return n * factorial(n - 1);
}
}
在Java进行阶乘计算中,使用 int n为13时相乘溢出,long 则是21。
------------------------------------------------------------------------------------
观察组合数计算公式(本人从初中开始就完全放飞自我、没有进修过数学,总之见谅)
C(n, m + 1) = n! / {(m + 1)!(n - m - 1)!}
= n! / {m!(n - m)!(m + 1) / (n - m)}
= C(n, m) / (m + 1) * (n - m)
如果有读者在网络上搜寻到有关,展开吧,请评论或私信告诉我,感激不尽。
上源码:
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
for (int i = 0, n = sc.nextInt(); i < n; i++) {
long num = 1;
for (int j = 0; j < i; num = num * (i - j) / (j + 1), j++) System.out.print(num + " ");
System.out.print("1\n");
}
}
}
这里便不测试 num 的阈值,用 long 就完事了
fine.
BASIC-7 特殊的数字
问题描述
153是一个非常特殊的数,它等于它的每位数字的立方和,即153=111+555+333。编程求所有满足这种条件的三位十进制数。
输出格式
按从小到大的顺序输出满足条件的三位十进制数,每个数占一行。
描述正在逐步简短
源码:
public class Main {
public static void main(String[] args) {
int[] cube = new int[10];
for (int i = 1; i < 10; i++) cube[i] = i * i * i;
for (int i = 1, j, l, num = 100; i < 10; i++)
for (j = 0; j < 10; j++)
for (l = 0; l < 10; l++, num++)
if (cube[i] + cube[j] + cube[l] == num) System.out.println(num);
}
}
硬遍历,想不出什么改进的法子。
BASIC-8 回文数
问题描述
1221是一个非常特殊的数,它从左边读和从右边读是一样的,编程求所有这样的四位十进制数。
输出格式
按从小到大的顺序输出满足条件的四位十进制数。
源码:
public class Main {
public static void main(String[] args) {
char[] four = new char[4];
for (char i = '1'; i <= '9'; i++) {
four[0] = four[3] = i;
for (char j = '0'; j <= '9'; j++) {
four[1] = four[2] = j;
System.out.println(four);
}
}
}
}
简单题,过
BASIC-9 特殊回文数
问题描述
123321是一个非常特殊的数,它从左边读和从右边读是一样的。
输入一个正整数n, 编程求所有这样的五位和六位十进制数,满足各位数字之和等于n 。
输入格式
输入一行,包含一个正整数n。
输出格式
按从小到大的顺序输出满足条件的整数,每个整数占一行。
测试样例
输入:
52
输出:
899998
989989
998899
数据规模与约定
1<=n<=54
import java.io.PrintWriter;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
PrintWriter out = new PrintWriter(System.out);
int n = sc.nextInt();
boolean isEven = (n & 1) != 1;
for (int i = 1,var = n - 2, cont = isEven? 36: 27, mid = isEven? 18: 9; var >= 0 && i < 10; i++, var -= 2) {
if (var > cont) continue;
for (int j = 0, var2 = var; j < 10 && var >= 0; j++, var2 -= 2) {
if (var2 > mid) continue;
if (var2 < 10) System.out.println(i + "" + j + "" + var2 + j + "" + i);
if (isEven) out.println(i + "" + j + "" + var2 / 2 + "" + var2 / 2 + j + "" + i);
}
}
out.close();
}
}
经典暴力解,不过加了几个判断条件让程序输入接近值域两端时更迅速。
BASIC-10 十进制转十六进制
问题描述
十六进制数是在程序设计时经常要使用到的一种整数的表示方式。它有0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F共16个符号,分别表示十进制数的0至15。十六进制的计数方法是满16进1,所以十进制数16在十六进制中是10,而十进制的17在十六进制中是11,以此类推,十进制的30在十六进制中是1E。
给出一个非负整数,将它表示成十六进制的形式。
输入格式
输入包含一个非负整数a,表示要转换的数。
输出格式
输出这个整数的16进制表示
测试样例
输入:
30
输出:
1E
数据规模与约定
0<=a<=2147483647
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
System.out.println(Integer.toHexString(sc.nextInt()));
}
}
一般来讲用 Integer API 就行,但该题评测数据中10 - 15皆是用大写字母表示
所以 复写to方法:
import java.util.Scanner;
public class Main {
static final char[] hex = {'0', '1', '2', '3', '4', '5', '6', '7', '8', '9', 'A', 'B', 'C', 'D', 'E', 'F'};
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt(), index = 8;
char[] out = new char[8];
do out[--index] = hex[n & 0xF];
while ((n >>>= 4) != 0);
System.out.println(out);
}
}
进制转换这不是老生常谈的东西 . . .
BASIC-11 十六进制转十进制
问题描述
从键盘输入一个不超过8位的正的十六进制数字符串,将它转换为正的十进制数后输出。
注:十六进制数中的10~15分别用大写的英文字母A、B、C、D、E、F表示。
测试样例
输入:
FFFF
输出:
65535
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
System.out.println(Integer.parseInt(sc.next(), 0x10));
}
}
值得注意的是,计算机存储有符号数引入了补码的方式,由于Java里没有无符号类型,所以32位的 int 最多只能接收 0x7FFFFFFF(-0X80000000) 这样的常量,这显然不满足题目需求
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
String hex = sc.next();
int index = hex.length(), offset = -4;
long out = 0, bit4;
while (index > 0){
if ((bit4 = hex.charAt(--index)) >= 'A') bit4 -= '7';
else bit4 -= '0';
out |= bit4 << (offset += 4);
}
System.out.println(out);
}
}
Java中左移运算是会忽略掉符号位的,省略(谜语人)百余字
BASIC-12 十六进制转八进制
问题描述
给定n个十六进制正整数,输出它们对应的八进制数。
输入格式
输入的第一行为一个正整数n (1<=n<=10)。
接下来n行,每行一个由0~9、大写字母A~F组成的字符串,表示要转换的十六进制正整数,每个十六进制数长度不超过100000。
输出格式
输出n行,每行为输入对应的八进制正整数。
测试样例
输入:
2
39
123ABC
输出:
71
4435274
import java.util.Scanner;
public class Main {
static String[] hex = {"0000", "0001", "0010", "0011", "0100", "0101", "0110", "0111", "1000", "1001", "", "", "", "", "", "", "","1010", "1011", "1100", "1101", "1110", "1111"};
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
StringBuilder out = new StringBuilder();
int n = sc.nextInt();
while (n-- > 0) {
String line = sc.next();
StringBuilder binary = new StringBuilder();
for (int i = 0, l = line.length(); i < l; i++) binary.append(hex[line.charAt(i) - '0']);
int len = binary.length(), offset = len % 3;
switch (offset) {
case 0: if (binary.charAt(0) == '0' && binary.charAt(1) == '0' && binary.charAt(2) == '0') offset = 3; break;
case 1: if (binary.charAt(0) != '0') out.append(1); break;
case 2: if (binary.charAt(0) != '0' || binary.charAt(1) != '0') out.append(Integer.valueOf(binary.substring(0, 2), 2));
}
while (offset < len) out.append(Integer.valueOf(binary.substring(offset, (offset += 3)), 2));
out.append('\n');
}
System.out.println(out);
}
}
想着尽量避免字符串增改,当然有很大一部分是避免不了的,写着写着就成这样。
评测数据: in 141,165 Byte
out 188,215 Byte
尽管不是第一次实现,但我最终还是跑了 5 遍才跑出结果(原因出在 case 没有跳出上)
再就是 二进制对八进制的转换,由于Java 7(蓝桥杯中开发环境为JDK 1.6)过后switch才支持比较String类型,所以也没有想出什么值得去做的法子。
当然 装模作样的 写个方法:
static int bit3toInt(String num) { return ((num.charAt(0) & 1) << 2) + ((num.charAt(1) & 1) << 1) + (num.charAt(2) & 1); }
还是没有问题的
再者就是把该方法替换到程序里面,测试性能

啊,结果便是性能有较大的提升
当然这个提升并不来自于这个方法
// line:19
case 2: if (binary.charAt(0) != '0' || binary.charAt(1) != '0') out.append(((binary.charAt(0) & 1) << 1) + (binary.charAt(1) & 1));
// line: 21
for (; offset < len; offset += 3) out.append(((binary.charAt(offset) & 1) << 2) + ((binary.charAt(offset + 1) & 1) << 1) + (binary.charAt(offset + 2) & 1));

tr0 为替换方法后的评测详情
tr1 为替换算式后的评测详情
tr2 为原版的评测详情
推测是源码的一个较大内存消耗点在于频繁的使用String.substring()方法
就这样
fine.
BASIC-13 数列排序
问题描述
给定一个长度为n的数列,将这个数列按从小到大的顺序排列。
输入格式
第一行为一个整数n。
第二行包含n个整数,为待排序的数,每个整数的绝对值小于10000。
输出格式
输出一行,按从小到大的顺序输出排序后的数列。
测试样例
输入:
5
8 3 6 4 9
输出:
3 4 6 8 9
数据规模与约定
1<=n<=200
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int[] arrays = new int[n];
for (int i = 0; i < n; i++) arrays[i] = sc.nextInt();
java.util.Arrays.sort(arrays);
for (int i = 0; i < n; i++) System.out.print(arrays[i] + " ");
}
}
Arrays.sort(),好使
该方法会在处理不同长度的数组时选择不同的排序方法,除非有学习或特殊需求,一般就用这个API就完事了
除了对数组进行排序,还可以构造有序数据结构
单向有序链表:
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
Node head = new Node(sc.nextInt());
for (int i = 1; i < n; i++) {
int value = sc.nextInt();
Node cur = head;
Node curLift = head;
while (cur.next != null)
if (value < cur.value) break;
else {
curLift = cur;
cur = cur.next;
}
if (cur.value < value) cur.next = new Node(value);
else if (cur != head) curLift.next = new Node(value, cur);
else head = new Node(value, head);
}
for (int i = 0; i < n; i++) {
System.out.print(head.value + " ");
head = head.next;
}
}
static class Node {
int value = 0;
Node next;
Node(int n) { this(n, null); }
Node(int n, Node next) {
this.value = n;
this.next = next;
}
}
}
第一次实现链表,插入方法直接覆盖到主程序的迭代中了,如有不足请多多指教。
目前还没有什么能力具体去比较二者之间的性能(各式各样的排序方法实在是太多),就这样。
BASIC-14 时间转换
问题描述
给定一个以秒为单位的时间t,要求用“
: : ”的格式来表示这个时间。表示时间, 表示分钟,而 表示秒,它们都是整数且没有前导的“0”。例如,若t=0,则应输出是“0:0:0”;若t=3661,则输出“1:1:1”。
输入格式
输入只有一行,是一个整数t。
输出格式
输出只有一行,是以“
: : ”的格式所表示的时间,不包括引号。
测试样例1
输入:
0
输出:
0:0:0
测试样例2
输入:
5436
输出:
1:30:36
数据规模与约定
0<=t<=86399
首先是Java的原生API:
import java.text.SimpleDateFormat;
import java.util.Date;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
System.out.println(new SimpleDateFormat("H:m:s").format(new Date((16 * 60 * 60 + sc.nextInt()) * 1000)));
}
}
Java Date 类可以接受一个Long类型变量来表示时间,该参数是从08:00:00 CST 1970 起的毫秒数。
所以要加上 16个小时的差值
SimpleDateFormat 是一个以语言环境敏感的方式来格式化和分析日期的类。SimpleDateFormat 允许你选择任何用户自定义日期时间格式来运行。
在该类中有的格式大写,有的格式小写,例如:HH 是 24 小时制,而 hh 是 12 小时制;MM 是月份,mm 是分。
12小时制不包含0,以前这对我来说不是常识,现在是的了。
当然刷题不能这么刷,程序功能越单一,一定程度上来说就更安全更迅速
blanc:
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int t = sc.nextInt();
System.out.println(t / 3600 + ":" + t / 60 % 60 + ":" + t % 60);
}
}
BASIC-15 字符串对比
问题描述
给定两个仅由大写字母或小写字母组成的字符串(长度介于1到10之间),它们之间的关系是以下4中情况之一:
1:两个字符串长度不等。比如 Beijing 和 Hebei
2:两个字符串不仅长度相等,而且相应位置上的字符完全一致(区分大小写),比如 Beijing 和 Beijing
3:两个字符串长度相等,相应位置上的字符仅在不区分大小写的前提下才能达到完全一致(也就是说,它并不满足情况2)。比如 beijing 和 BEIjing
4:两个字符串长度相等,但是即使是不区分大小写也不能使这两个字符串一致。比如 Beijing 和 Nanjing
编程判断输入的两个字符串之间的关系属于这四类中的哪一类,给出所属的类的编号。
输入格式
包括两行,每行都是一个字符串
输出格式
仅有一个数字,表明这两个字符串的关系编号
测试样例
输入:
BEIjing
beiJing
输出:
3
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
String arg1 = sc.next(), arg2 = sc.next();
int flag = 2;
if (arg1.length() != arg2.length()) flag = 1;
else for (int i = 0, l = arg1.length(); i < l; i++) {
int var = Math.abs(arg1.charAt(i) - arg2.charAt(i));
if (var != 0) {
if (var == 0x20) flag = 3;
else flag = 4;
break;
}
}
System.out.print(flag);
}
}
抬走抬走
BASIC-16 分解质因数
问题描述
求出区间[a,b]中所有整数的质因数分解。
输入格式
输入两个整数a,b。
输出格式
每行输出一个数的分解,形如k=a1a2a3…(a1<=a2<=a3…,k也是从小到大的)(具体可看样例)
测试样例
输入:
3 10
输出:
3=3
4=2*2
5=5
6=2*3
7=7
8=2*2*2
9=3*3
10=2*5
数据规模与约定
2<=a<=b<=10000
第一眼就觉得是个递归题:
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
for (int a = sc.nextInt(), b = sc.nextInt(); a <= b; a++) System.out.println(a + "=" + O(a, 2));
}
static String O(int n, int i) {
for (; i < n; i++) if (n % i == 0) return i + "*" + O(n / i, i);
return n + "";
}
}
但其实是没有递归的必要
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
for (int a = sc.nextInt(), b = sc.nextInt(), i = 2; a <= b; a++, i = 2){
System.out.print(a + "=");
for (int n = a; i < n;)
if (n % i == 0) {
n /= i;
System.out.print(i + "*");
} else i++;
System.out.print(i + "\n");
}
}
}
就蓝桥系统而言,递归比迭代强很多

tr0 与 tr4 为递归评测详情
其他 tr 为迭代
虽然蓝桥系统有时挺离谱的,但对这五次结果进行对比,有点出乎预料。
此时我了解了一下 Pollard Rho 因数分解
百度了一篇还可以的文档,但是要钱就没继续往下看了
还有就是 生成质数表 进行 优化:
import java.util.ArrayList;
import java.util.Scanner;
public class Main {
static ArrayList<Integer> list;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int a = sc.nextInt(), b = sc.nextInt();
list = new ArrayList<Integer>();
for (int i = 2; i <= b; i++) if (isPrime(i))list.add(i);
for (; a <= b; a++) System.out.println(a + "=" + O(a, 0));
}
static String O(int n, int i) {
int prime = 0;
for (int l = list.size(); i < l; i++) if (n % (prime = list.get(i)) == 0) break;
if (n == prime) return n + "";
return prime + "*" + O(n / prime, i);
}
static boolean isPrime(int n) {
double l = Math.sqrt(n);
for (int i = 2; i < l; i++) if (n % i == 0) return false;
return true;
}
}
多写这么多还是有显著提升的
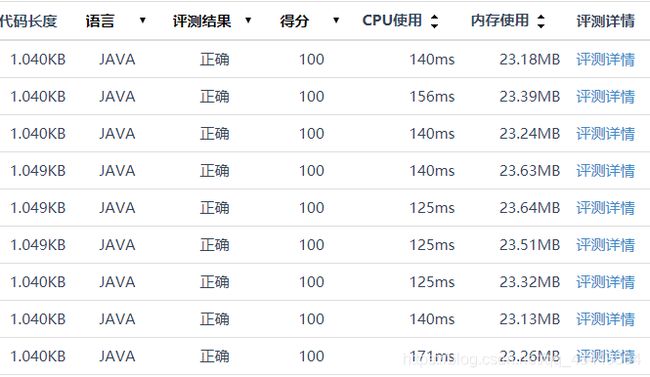
进行最后一个测试,看看迭代的性能是因频繁使用 System.out 而达不到理想水平

图中不同的版本各连续测试三次,均为使用质数表版本
改进方法为使用 StringBuilder 保存结果集
1 为递归不保存
2 为递归保存
3 为迭代不保存
4 为迭代保存
至此可以看到,在该复杂度下,迭代性能应略高递归一筹
而且经过对比可以发现,递归保存结果集后性能不增反减,如有资源详解它们之间的关系,性能逆差的点,请评论或私信告诉我,感激不尽
最后附上运行效能最快的源码:
import java.util.ArrayList;
import java.util.Scanner;
public class Main {
static ArrayList<Integer> list;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
StringBuilder out = new StringBuilder();
int a = sc.nextInt(), b = sc.nextInt();
list = new ArrayList<Integer>();
for (int i = 2; i <= b; i++) if (isPrime(i))list.add(i);
for (int l = list.size(); a <= b; a++) {
out.append(a + "=");
for (int i = 0, n = a; i < l;) {
int prime = list.get(i);
if (n % prime == 0) {
out.append(prime);
if ((n /= prime) != 1) out.append('*');
else break;
} else i++;
}
out.append('\n');
}
System.out.print(out);
}
static boolean isPrime(int n) {
double l = Math.sqrt(n);
for (int i = 2; i < l; i++) if (n % i == 0) return false;
return true;
}
}
没有什么改动,只是单纯的替换了输出而已
find.
BASIC-17 矩阵乘法
问题描述
给定一个N阶矩阵A,输出A的M次幂(M是非负整数)
例如:
A =
1 2
3 4
A的2次幂
7 10
15 22
输入格式
第一行是一个正整数N、M,表示矩阵A的阶数和要求的幂数
接下来N行,每行N个绝对值不超过10的非负整数,描述矩阵A的值
输出格式
输出共N行,每行N个整数,表示A的M次幂所对应的矩阵。相邻的数之间用一个空格隔开
测试样例
输入:
2 2
1 2
3 4
输出:
7 10
15 22
数据规模与约定
1<=N<=30, 0<=M<=5
源码:
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int N = sc.nextInt(), M = sc.nextInt();
int[][] A = new int[N][N];
int[][] power = new int[N][N];
if (M == 0)
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++)
if (i != j) System.out.print('0' + " ");
else System.out.print('1' + " ");
System.out.print('\n');
}
else {
for (int i = 0; i < N; i++)
for (int j = 0; j < N; j++)
power[i][j] = A[i][j] = sc.nextInt();
for (int m = 1; m < M; m++) {
int[][] temp = new int[N][N];
for (int i = 0; i < N; i++)
for (int j = 0; j < N; j++)
for (int k = 0; k < N; k++) temp[i][j] += A[i][k] * power[k][j];
power = temp;
}
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++)
System.out.print(power[i][j] + " ");
System.out.print('\n');
}
}
}
}
没有深入过矩阵乘法,所以就这样 . . .
记住 line 22 的三重循环就行
BASIC-18 矩形面积交
问题描述
平面上有两个矩形,它们的边平行于直角坐标系的X轴或Y轴。对于每个矩形,我们给出它的一对相对顶点的坐标,请你编程算出两个矩形的交的面积。
输入格式
输入仅包含两行,每行描述一个矩形。
在每行中,给出矩形的一对相对顶点的坐标,每个点的坐标都用两个绝对值不超过10^7的实数表示。
输出格式
输出仅包含一个实数,为交的面积,保留到小数后两位。
测试样例
输入:
1 1 3 3
2 2 4 4
输出:
1.00
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
double A1x = sc.nextDouble(),
A1y = sc.nextDouble(),
A2x = sc.nextDouble(),
A2y = sc.nextDouble(),
B1x = sc.nextDouble(),
B1y = sc.nextDouble(),
B2x = sc.nextDouble(),
B2y = sc.nextDouble();
double X1 = max(min(A1x, A2x), min(B1x, B2x)),
X2 = min(max(A1x, A2x), max(B1x, B2x)),
Y1 = max(min(A1y, A2y), min(B1y, B2y)),
Y2 = min(max(A1y, A2y), max(B1y, B2y));
if (X2 > X1 && Y2 > Y1) System.out.printf("%.2f", (X2 - X1) * (Y2 - Y1));
else System.out.println("0.00");
}
static double min(double var, double var1) { return var <= var1 ? var : var1; }
static double max(double var, double var1) { return var >= var1 ? var : var1; }
}
这题也没啥好说的,除了代码看起来像屎块一样
BASIC-19 完美的代价
问题描述
回文串,是一种特殊的字符串,它从左往右读和从右往左读是一样的。小龙龙认为回文串才是完美的。现在给你一个串,它不一定是回文的,请你计算最少的交换次数使得该串变成一个完美的回文串。
交换的定义是:交换两个相邻的字符
例如mamad
第一次交换 ad : mamda
第二次交换 md : madma
第三次交换 ma : madam (回文!完美!)
输入格式
第一行是一个整数N,表示接下来的字符串的长度(N <= 8000)
第二行是一个字符串,长度为N.只包含小写字母
输出格式
如果可能,输出最少的交换次数。
否则输出Impossible
测试样例
输入:
5
mamad
输出:
3
首先是在 Project 里找到的初版:
我觉得很好去理解这个题所以就把它放出来了
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int N = sc.nextInt();
StringBuilder firsthand = new StringBuilder(sc.next());
int weight[] = new int[26], isOdd = 0, meter = 0, lastIndex;
for (int i = 0; i < N; i++) weight[firsthand.charAt(i) - 'a']++;
for (int i = 0; i < 26; i++) if((weight[i] & 1) == 1) isOdd++;
if (isOdd > 1) {
System.out.println("Impossible");
return;
}
while (N > 1) {
lastIndex = firsthand.lastIndexOf(firsthand.charAt(0) + "");
if (lastIndex == 0) {
firsthand.insert(2, firsthand.charAt(0));
firsthand.deleteCharAt(0);
meter++;
} else {
firsthand.deleteCharAt(lastIndex);
firsthand.deleteCharAt(0);
meter += N - 1 - lastIndex;
N -= 2;
}
}
System.out.println(meter);
}
}
消消乐(并没玩过 )
首先要避免的点就是对字符串大量的删改
其次再避免掉一部分特殊判断
import java.util.Scanner;
public class Main {
static char[] str;
static int strlastIndex;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int N = sc.nextInt(), cur, cnt = 0; strlastIndex = N - 1;
str = sc.next().toCharArray();
int flag = N & 1 ^ 1;
for (int i = 0; i < strlastIndex; i++) {
if ((cur = lastIndexOf(i)) != i) {
cnt += strlastIndex - cur;
while (cur < strlastIndex) {
char temp = str[cur];
str[cur] = str[++cur];
str[cur] = temp;
}
strlastIndex--;
} else {
if (++flag > 1) break;
cnt += N / 2 - i;
}
}
if (flag <= 1) System.out.println(cnt);
else System.out.println("Impossible");
}
static int lastIndexOf(int index) {
for (int i = strlastIndex, j = index; i > j; i--) if (str[i] == str[index]) return i;
return index;
}
}
好,我们可以看到性能并没有提升,过
BASIC-20 数的读法
问题描述
Tom教授正在给研究生讲授一门关于基因的课程,有一件事情让他颇为头疼:一条染色体上有成千上万个碱基对,它们从0开始编号,到几百万,几千万,甚至上亿。
比如说,在对学生讲解第1234567009号位置上的碱基时,光看着数字是很难准确的念出来的。
所以,他迫切地需要一个系统,然后当他输入12 3456 7009时,会给出相应的念法:
十二亿三千四百五十六万七千零九
用汉语拼音表示为
shi er yi san qian si bai wu shi liu wan qi qian ling jiu
这样他只需要照着念就可以了。
你的任务是帮他设计这样一个系统:给定一个阿拉伯数字串,你帮他按照中文读写的规范转为汉语拼音字串,相邻的两个音节用一个空格符格开。
注意必须严格按照规范,比如说“10010”读作“yi wan ling yi shi”而不是“yi wan ling shi”,“100000”读作“shi wan”而不是“yi shi wan”,“2000”读作“er qian”而不是“liang qian”。
输入格式
有一个数字串,数值大小不超过2,000,000,000。
输出格式
是一个由小写英文字母,逗号和空格组成的字符串,表示该数的英文读法。
测试样例
输入:
1234567009
输出:
shi er yi san qian si bai wu shi liu wan qi qian ling jiu
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
StringBuilder toNum = new StringBuilder();
String num = sc.next();
String[] digits = {"ling ", "yi ", "er ", "san ", "si ", "wu ", "liu ", "qi ", "ba ", "jiu "};
String[] decimal = { "", "shi ", "bai ", "qian ", "wan ", "shi ", "bai ", "qian ", "yi ", "shi "};
boolean aboveIsZero = false;
int ones = num.length() - 1, i = 0;
if (num.charAt(0) == '1' && ones % 4 == 1) toNum.append(decimal[++i]);
for (char cur; i <= ones; i++)
if ((cur = num.charAt(i)) == '0') {
if (!aboveIsZero)toNum.append(digits[0]);
aboveIsZero = true;
} else {
toNum.append(digits[cur - '0'] + decimal[ones - i]);
aboveIsZero = false;
}
if (aboveIsZero && ones > 0) toNum.delete(toNum.length() - 5, toNum.length());
System.out.println(toNum);
}
}
特判,读,特判
我为什么是个废物呢
BASIC-21 Sine之舞
问题描述
最近FJ为他的奶牛们开设了数学分析课,FJ知道若要学好这门课,必须有一个好的三角函数基本功。所以他准备和奶牛们做一个“Sine之舞”的游戏,寓教于乐,提高奶牛们的计算能力。
不妨设
An=sin(1–sin(2+sin(3–sin(4+…sin(n))…)
Sn=(…(A1+n)A2+n-1)A3+…+2)An+1
FJ想让奶牛们计算Sn的值,请你帮助FJ打印出Sn的完整表达式,以方便奶牛们做题。
输入格式
仅有一个数:N。
输出格式
请输出相应的表达式Sn,以一个换行符结束。输出中不得含有多余的空格或换行、回车符。
测试样例
输入:
3
输出:
((sin(1)+3)sin(1–sin(2))+2)sin(1–sin(2+sin(3)))+1
数据规模与约定
N<201
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
System.out.println(SLift(sc.nextInt(), 1));
}
static String A(int i, int j) {
if (i == j) return "sin(" + j + ")";
return "sin(" + j + ((j & 1) == 0? "+": "-") + A(i, j + 1) + ")";
}
static String S(int i, int j) {
if (i == j) return A(j, 1) + "+1";
return A(j, 1) + "+" + (i - j + 1) + ")" + S(i, j + 1);
}
static String SLift(int N, int i) {
if (N - i == 0) return S(N, 1);
return '(' + SLift(N, i + 1);
}
}
反正多写个递归在我看来是省事了的,过
BASIC-22 FJ的字符串
问题描述
FJ在沙盘上写了这样一些字符串:
A1 = “A”
A2 = “ABA”
A3 = “ABACABA”
A4 = “ABACABADABACABA”
… …
你能找出其中的规律并写所有的数列AN吗?
输入格式
仅有一个数:N
输出格式
请输出相应的字符串AN,以一个换行符结束。输出中不得含有多余的空格或换行、回车符。
测试样例
输入:
3
输出:
ABACABA
数据规模与约定
N ≤ 26
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
System.out.println(AN(sc.nextInt()));
}
static String AN(int n) {
if (n == 1) return "A";
return AN(n - 1) + (char)(0x40 + n) + AN(n - 1);
}
}
这题比上题简单多了,过
BASIC-23 芯片测试
问题描述
有 n 块芯片,有好有坏,已知好芯片比坏芯片多。
每个芯片都能用来测试其他芯片。用好芯片测试其他芯片时,能正确给出被测试芯片是好还是坏。而用坏芯片测试其他芯片时,会随机给出好或是坏的测试结果(即此结果与被测试芯片实际的好坏无关)。
给出所有芯片的测试结果,问哪些芯片是好芯片。
输入格式
输入数据第一行为一个整数n,表示芯片个数。
第二行到第n+1行为n*n的一张表,每行n个数据。表中的每个数据为0或1,在这n行中的第i行第j列(1≤i, j≤n)的数据表示用第i块芯片测试第j块芯片时得到的测试结果,1表示好,0表示坏,i=j时一律为1(并不表示该芯片对本身的测试结果。芯片不能对本身进行测试)。
输出格式
按从小到大的顺序输出所有好芯片的编号
测试样例
输入:
3
1 0 1
0 1 0
1 0 1
输出:
1 3
数据规模与约定
2≤n≤20
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int N = sc.nextInt();
int[] No = new int[N];
for (int i = 0; i < N; i++)
for (int j = 0; j < N; j++) No[j] += sc.nextInt();
for (int i = 0, j = N / 2; i < N;) if (No[i++] > j) System.out.print(i + " ");
}
}
过过过过过
BASIC-24 龟兔赛跑预测
问题描述
话说这个世界上有各种各样的兔子和乌龟,但是研究发现,所有的兔子和乌龟都有一个共同的特点——喜欢赛跑。于是世界上各个角落都不断在发生着乌龟和兔子的比赛,小华对此很感兴趣,于是决定研究不同兔子和乌龟的赛跑。他发现,兔子虽然跑比乌龟快,但它们有众所周知的毛病——骄傲且懒惰,于是在与乌龟的比赛中,一旦任一秒结束后兔子发现自己领先t米或以上,它们就会停下来休息s秒。对于不同的兔子,t,s的数值是不同的,但是所有的乌龟却是一致——它们不到终点决不停止。
然而有些比赛相当漫长,全程观看会耗费大量时间,而小华发现只要在每场比赛开始后记录下兔子和乌龟的数据——兔子的速度v1(表示每秒兔子能跑v1米),乌龟的速度v2,以及兔子对应的t,s值,以及赛道的长度l——就能预测出比赛的结果。但是小华很懒,不想通过手工计算推测出比赛的结果,于是他找到了你——清华大学计算机系的高才生——请求帮助,请你写一个程序,对于输入的一场比赛的数据v1,v2,t,s,l,预测该场比赛的结果。
输入格式
输入只有一行,包含用空格隔开的五个正整数 v1,v2,t,s,l
输出格式
输出包含两行,第一行输出比赛结果——一个大写字母“T”或“R”或“D”,分别表示乌龟获胜,兔子获
第二行输出一个正整数,表示获胜者(或者双方同时)到达终点所耗费的时间(秒数)。
测试样例1
输入:
10 5 5 2 20
输出:
D
4
测试样例2
输入:
10 5 5 1 20
输出:
R
3
测试样例3
输入:
10 5 5 3 20
输出:
T
4
数据规模与约定
v1, v2<=100, t<=300, s<=10, l<=10000且为v1,v2的公倍数
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int v1 = sc.nextInt(), v2 = sc.nextInt(), t = sc.nextInt(), s = sc.nextInt(), l = sc.nextInt();
int vs = l / v2, v1t = 0, v2t = 0;
char flag = 'T';
for (int i = 0; i <= vs; i++) {
if (v1t >= l) {
if (i == vs) flag = 'D';
else flag = 'R';
vs = i;
break;
}
if (v1t >= v2t + t) v1t -= v1 * s;
v1t += v1;
v2t += v2;
}
System.out.print(flag + "\n" + vs);
}
}
抽象了一下问题,但也没什么好说的,过
BASIC-25 回形取数
问题描述
回形取数就是沿矩阵的边取数,若当前方向上无数可取或已经取过,则左转90度。一开始位于矩阵左上角,方向向下。
输入格式
输入第一行是两个正整数m, n,表示矩阵的行和列。接下来m行每行n个整数,表示这个矩阵。
输出格式
输出只有一行,共mn个数,为输入矩阵回形取数得到的结果。数之间用一个空格分隔,行末不要有多余的空格。
测试样例
输入:
3 3
1 2 3
4 5 6
7 8 9
输出:
1 4 7 8 9 6 3 2 5
数据规模与约定
1<=m<=200, 1<=n<=200
尝试着学了下,发现以我的能力还不足以同事应付极端数据和减少特殊判断
最后修正的思路和一年前一样
呜呜呜,我是five
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int m = sc.nextInt(), n = sc.nextInt(), mIsOdd = m & 1;
int[][] mat = new int[m][n];
for (int i = 0; i < m; i++)
for (int j = 0; j < n; j++)
mat[i][j] = sc.nextInt();
StringBuilder out = new StringBuilder();
for (int i = 0, j = 0, l = m < n? m / 2 + mIsOdd: (n & 1) == 1? (n / 2) + 1: n / 2, offset = 0; offset < l; i = j = ++offset) {
while (i < m - offset) out.append(mat[i++][j] + " ");
if (++j < n - offset) {
for (i--; j < n - offset;)
out.append(mat[i][j++] + " ");
for (j--, i--; i > offset;)
out.append(mat[i--][j] + " ");
}
if (j == n - offset - 1 && i != m - offset - 1 - mIsOdd) while (j > offset) out.append(mat[i][j--] + " ");
}
System.out.println(out);
}
}
BASIC-26 报时助手
问题描述
给定当前的时间,请用英文的读法将它读出来。
时间用时h和分m表示,在英文的读法中,读一个时间的方法是:
如果m为0,则将时读出来,然后加上“o’clock”,如3:00读作“three o’clock”。
如果m不为0,则将时读出来,然后将分读出来,如5:30读作“five thirty”。
时和分的读法使用的是英文数字的读法,其中0~20读作:
0:zero, 1: one, 2:two, 3:three, 4:four, 5:five, 6:six, 7:seven, 8:eight, 9:nine, 10:ten, 11:eleven, 12:twelve, 13:thirteen, 14:fourteen, 15:fifteen, 16:sixteen, 17:seventeen, 18:eighteen, 19:nineteen, 20:twenty。
30读作thirty,40读作forty,50读作fifty。
对于大于20小于60的数字,首先读整十的数,然后再加上个位数。如31首先读30再加1的读法,读作“thirty one”。
按上面的规则21:54读作“twenty one fifty four”,9:07读作“nine seven”,0:15读作“zero fifteen”。
输入格式
输入包含两个非负整数h和m,表示时间的时和分。非零的数字前没有前导0。h小于24,m小于60。
输出格式
输出时间时刻的英文。
测试样例
输入:
0 15
输出:
zero fifteen
import java.util.Scanner;
public class Main {
static String[] clock = {"zero ", "one ", "two ", "three ", "four ", "five ", "six ", "seven ", "eight ", "nine ", "ten ", "eleven ", "twelve ", "thirteen ", "fourteen ", "fifteen ", "sixteen ", "seventeen ", "eighteen ", "nineteen ", "twenty ", "thirty ", "forty ", "fifty ", "o'clock "};
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int h = sc.nextInt(), m = sc.nextInt();
if (m == 0) System.out.print(toSay(h) + clock[24]);
else System.out.print(toSay(h) + toSay(m));
}
static String toSay(int n) {
if (n <= 20) return clock[n];
if (n % 10 == 0) return clock[n / 10 + 18];
return clock[n / 10 + 18] + clock[n % 10];
}
}
过
BASIC-27 2n皇后问题
问题描述
给定一个n*n的棋盘,棋盘中有一些位置不能放皇后。现在要向棋盘中放入n个黑皇后和n个白皇后,使任意的两个黑皇后都不在同一行、同一列或同一条对角线上,任意的两个白皇后都不在同一行、同一列或同一条对角线上。问总共有多少种放法?
输入格式
输入的第一行为一个整数n,表示棋盘的大小。
接下来n行,每行n个0或1的整数,如果一个整数为1,表示对应的位置可以放皇后,如果一个整数为0,表示对应的位置不可以放皇后。
输出格式
输出一个整数,表示总共有多少种放法。
测试样例1
输入:
4
1 1 1 1
1 1 1 1
1 1 1 1
1 1 1 1
输出:
2
测试样例2
输入:
4
1 0 1 1
1 1 1 1
1 1 1 1
1 1 1 1
输出:
0
数据规模与约定
n <= 8
import java.util.Scanner;
public class Main {
static int n, map[][], cnt = 0, defQueen = 2, space = 1;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt(); map = new int[n][n];
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++) map[i][j] = sc.nextInt();
Queen(defQueen, 0);
System.out.println(cnt);
}
static void Queen(int queen, int y) {
if (y == n){
if (queen == defQueen) Queen(queen + 1, 0);
else cnt++;
} else for (int x = 0; x < n; x++) {
if (Can(y, x, queen)) map[y][x] = queen;
else continue;
Queen(queen, y + 1);
map[y][x] = space;
}
}
static boolean Can(int y, int x, int queen) {
if (map[y][x] != space) return false;
for (int i = y - 1; i >= 0; i--) if (map[i][x] == queen) return false;
for (int i = y - 1, j = x - 1; i >= 0 && j >= 0; j--, i--) if (map[i][j] == queen) return false;
for (x++, y--; y >= 0 && x < n; y--, x++) if (map[y][x] == queen) return false;
return true;
}
}
非常经典的递归回溯问题,过
BASIC-28 Huffuman树
问题描述
Huffman树在编码中有着广泛的应用。在这里,我们只关心Huffman树的构造过程。
给出一列数{pi}={p0, p1, …, pn-1},用这列数构造Huffman树的过程如下:
1. 找到{pi}中最小的两个数,设为pa和pb,将pa和pb从{pi}中删除掉,然后将它们的和加入到{pi}中。这个过程的费用记为pa + pb。
2. 重复步骤1,直到{pi}中只剩下一个数。
在上面的操作过程中,把所有的费用相加,就得到了构造Huffman树的总费用。
本题任务:对于给定的一个数列,现在请你求出用该数列构造Huffman树的总费用。
例如,对于数列{pi}={5, 3, 8, 2, 9},Huffman树的构造过程如下:
1. 找到{5, 3, 8, 2, 9}中最小的两个数,分别是2和3,从{pi}中删除它们并将和5加入,得到{5, 8, 9, 5},费用为5。
2. 找到{5, 8, 9, 5}中最小的两个数,分别是5和5,从{pi}中删除它们并将和10加入,得到{8, 9, 10},费用为10。
3. 找到{8, 9, 10}中最小的两个数,分别是8和9,从{pi}中删除它们并将和17加入,得到{10, 17},费用为17。
4. 找到{10, 17}中最小的两个数,分别是10和17,从{pi}中删除它们并将和27加入,得到{27},费用为27。
5. 现在,数列中只剩下一个数27,构造过程结束,总费用为5+10+17+27=59。
输入格式
输入的第一行包含一个正整数 n。
接下来是n个正整数,表示 p0, p1, …, pn-1,每个数不超过1000。
输出格式
输出用这些数构造Huffman树的总费用。
测试样例
输入:
5
5 3 8 2 9
输出:
59
数据规模与约定
n<=100
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt(), price = 0, added;
int[] coding = new int[n + (n & 1)];
for (int i = 0; i < n; i++) coding[i] = sc.nextInt();
java.util.Arrays.sort(coding, 0, n);
for (int i = 0, l = n - 1; i < l; i++) {
price += added = coding[i + 1] += coding[i];
for (int j = i + 2; j < n; j++)
if (added > coding[j]) {
coding[j - 1] = coding[j];
coding[j] = added;
} else break;
}
System.out.print(price);
}
}
懒一点的可以全程使用 Arrays.sort()
不过这样势必会浪费很多资源
BASIC-29 高精度加法
问题描述
输入两个整数a和b,输出这两个整数的和。a和b都不超过100位。
算法描述
由于a和b都比较大,所以不能直接使用语言中的标准数据类型来存储。对于这种问题,一般使用数组来处理。
定义一个数组A,A[0]用于存储a的个位,A[1]用于存储a的十位,依此类推。同样可以用一个数组B来存储b。
计算c = a + b的时候,首先将A[0]与B[0]相加,如果有进位产生,则把进位(即和的十位数)存入r,把和的个位数存入C[0],即C[0]等于(A[0]+B[0])%10。然后计算A[1]与B[1]相加,这时还应将低位进上来的值r也加起来,即C[1]应该是A[1]、B[1]和r三个数的和.如果又有进位产生,则仍可将新的进位存入到r中,和的个位存到C[1]中。依此类推,即可求出C的所有位。
最后将C输出即可。
输入格式
输入包括两行,第一行为一个非负整数a,第二行为一个非负整数b。两个整数都不超过100位,两数的最高位都不是0。
输出格式
输出一行,表示a + b的值。
测试样例
输入:
20100122201001221234567890
2010012220100122
输出:
20100122203011233454668012
BigInteger:
import java.math.BigInteger;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
BigInteger a = new BigInteger(sc.next()), b = new BigInteger(sc.next());
System.out.println(a.add(b));
}
}
自己实现:
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
char[] a = sc.next().toCharArray(), b = sc.next().toCharArray();
if (a.length < b.length) {
char[] temp = a;
a = b;
b = temp;
}
int offset = a.length - b.length, carry = 0, i;
for (i = a.length - 1; i >= offset; i--)
if ((a[i] += (b[i - offset] & 0xF) + carry) > '9') {
a[i] -= 10;
carry = 1;
} else carry = 0;
while (carry == 1 && i >= 0)
if ((a[i] += carry) > '9') a[i--] = '0';
else carry = 0;
if (carry == 1) System.out.print(1);
System.out.print(a);
}
}
这么写个 while 是为了代码美观,老实说把我给丑哭了
用 (“0” + sc.next()).toCharArray() 这种方式优化了一下,然后觉得自己是个傻逼,过
BASIC-30 阶乘计算
问题描述
输入一个正整数n,输出n!的值。
其中n!=123*…*n。
算法描述
n!可能很大,而计算机能表示的整数范围有限,需要使用高精度计算的方法。使用一个数组A来表示一个大整数a,A[0]表示a的个位,A[1]表示a的十位,依次类推。
将a乘以一个整数k变为将数组A的每一个元素都乘以k,请注意处理相应的进位。
首先将a设为1,然后乘2,乘3,当乘到n时,即得到了n!的值。
输入格式
输入包含一个正整数n,n<=1000。
输出格式
输出n!的准确值。
测试样例
输入:
10
输出:
3628800
BigInteger:
import java.math.BigInteger;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
if (n < 21) System.out.print(factorial(n));
else System.out.println(factorialNumGTR21(n));
}
static BigInteger factorialNumGTR21(int n) {
if (n <= 1) return BigInteger.ONE;
return new BigInteger(Integer.toString(n)).multiply(factorialNumGTR21(n - 1));
}
static long factorial(int n) {
if (n <= 1) return 1;
return n * factorial(n - 1);
}
}
fine.
附: 入门训练
直接水代码了
BEGIN-1:
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
System.out.println(sc.nextInt() + sc.nextInt());
}
}
BEGIN-2:
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
long n = sc.nextInt();
System.out.println((n + 1) * n / 2);
}
}
BEGIN-3:
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
System.out.printf("%.7f", Math.pow(sc.nextInt(), 2) * Math.PI);
}
}
BEGIN-4:
import java.util.Scanner;
public class Main {
static final int mod = 10007;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt() - 2, F1, F2, F3;
F1 = F2 = F3 = 1;
while (n-- > 0) F2 = F3 = (F1 + (F1 = F2)) % mod;
System.out.println(F3);
}
}
递归,不过时间复杂度不能胜任这个问题
public class Main {
static final int mod = 10007;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
System.out.println(sail(sc.nextInt()));
}
static int sail(int n) {
if (n <= 2) return 1;
return (sail(n - 1) + sail(n - 2)) % mod;
}
}