Kaldi WFST最小化算法

1. WFST最小化算法

最小化算法主要是在保证DFA识别的语言不变的条件下，将DFA中等价状态合并，减少状态数、转移边数，简化DFA结构，从而减少存储空间和运算时间。比较有名的最小化算法有Moore，Hopcroft以及Brzozowski等，本章主要针对Hopcroft算法进行优化。WFST Hopcroft最小化算法原理

Hopcroft算法在初始阶段将所有状态划分为终结状态和非终结状态两个等价类，然后不断地根据分割集合对等价类进行分割，将状态集合划分为既不重叠又不为空的状态子集，直到所有等价类都无法继续拆分。其算法伪代码如图 6所示。

 

图 6 WFST Hopcroft算法伪代码

最小化结束后，同一个子集中的所有状态是相等的，他们接受相同“input : output / weight”，最后用状态子集中的某一个具体的状态代表该状态子集即可。

初始时，原始的Hopcroft算法将状态集分为终止状态集合非终止状态集合；针对WFST，需要继续根据终止状态的权重进行深入划分，因为，不同权重的终止状态显然属于不同的等价类；同时原始的Hopcroft主要是针对FSA的，而FSA只有一个输入Label，而WFST有“input : output / weight”，所以在进行集合划分是需要将“input : output / weight”看做一个整体来进行状态子集的划分，可以使用hash表等数据结构来实现。

Kaldi Hopcroft算法流程

上面叙述的是WFST中Hopcroft算法的原理，在实现时，Kaldi中采用了一些额外的小技巧。

编码

上文中说道，因为原始的Hopcroft算法是针对FSA的，所以在处理WFST时，首先针对具有不同权重的终止状态，需要将其当做不同的终止状态，不能合并在一起；其次需要将“input : output / weight”看做一个整体。

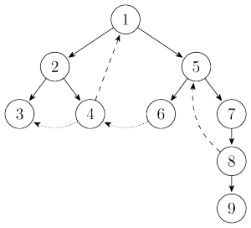
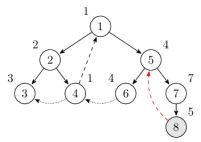
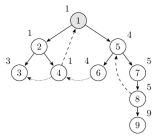
我们以图 7(a)所示作为例子，针对上面提到的问题，使用了两个不同的技巧，如图(b)所示。

 

(a)原始WFST

 

(b)编码后WFST

图 7 WFST编码例子

WFST中需要将“input : output / weight”看做一个整体，OpenFST中的做法是根据“input : output / weight”的出现顺序，查找hash表，如果其已经在hash表中存在，则返回对应的编号，若未在hash表中出现，则将其插入到hash表中，其编号值加1(注：编号是从1开始，hash表中第一个“input : output / weight”元组是1，第二个元组是2，以此类推)，所以(a)中“a:a/1”编号为1，“b:b/2”编号为2。同时，图(a)中{0，4，5，7，8，9}作为非终止状态集，{1，2，3，5，6}作为终止状态集，但是，状态3是一个权重为3的终止状态，而状态集{1，2，5，6}的权重都为0，所以，按照上面的讨论，需要将{3}和{1，2，5，6}作为不同的终止状态集；为了算法设计方便，OpenFST中新增加一个终止状态10，将状态1、2、3、5、6的“终止状态”这个属性转移到状态10上，并将状态1、2、3、5、6的权重作为指向终止状态的“边”的权重，如图(b)所示，由于状态1、2、5、6指向状态10的边都是“eps : eps / 0”，所以其编号为3，由于状态3的权重为3，所以，其指向状态10的边为“eps : eps / 3”，在hash表中的编号为4。使用如此两个小技巧即可完成WFST中最小化的编码。

最小化

最小化算法的核心部分涉及连通图运算、逆运算、最小化和状态合并四步，其中连通图运算时为了去除“Dead State”，逆运算是为了求某一个状态的输入边，最小化是核心运算，状态合并是为了合并等价的状态，减少状态数。

强连通分量

观察图 7(a)或者(b)都可以知道，其中的状态结点7和9都是不连通的状态结点，也即状态跳转到7或者9的时候，都将无法到达终止状态结点。为了消除这些结点对识别结果的影响，需要首先使用连通图算法删除这些不连通的结点，OpenFST中采用了Tarjan有向图强连通分量算法，下面大致叙述一下强连通分量算法。

在有向图G中，如果任意两个定点之间至少存在一条路径，称两个定点强连通；如果有向图中每两个定点都强连通，则称有向图G是一个强连通图；非强连通图中具有最多结点的强连通子图，称为强连通分量。如图 8(a)中，子图{1,2,4,5,6,7,8}是一个强连通分量，因为他们两两可达，{3}和{9}也分别是两个强连通分量，但{3}、{9}和{1,2,4,5,6,7,8}这三个强连通分量之间不能两两可达。

 

 

(a)原图                                                              (b)搜索树

图 8 强连通分量

Tarjan算法主要通过图的深度优先搜索算法。图(b)为原图对应的搜索树，有向图的搜索树中主要有四种边，其中用实线画出来的是树边（tree edge），每次搜索找到一个还没有访问过的结点的时候就形成了一条树边。用长虚线画出来的是反祖边（back edge），也被叫做回边。用短虚线画出来的是横叉边（cross edge），它主要是在搜索的时候遇到了一个已经访问过的结点，但是这个结点并不是当前节点的祖先时形成的。除此之外，像从结点1到结点6这样的边叫做前向边（forward edge），它是在搜索的时候遇到子树中的结点的时候形成的。

Tarjan 算法主要是在 DFS 的过程中维护了一些信息：dfn、low 和stack。stack里的元素表示的是当前已经访问过但是没有被归类到任一强连通分量的结点；dfn[u] 表示结点 u 在 DFS 中第一次搜索到的次序，通常被叫做时间戳；low[u] 稍微有些复杂，它表示从 u 或者以 u 为根的子树中的结点，再通过一条反祖边或者横叉边可以到达的时间戳最小的结点 v 的时间戳。

当通过 u 搜索到一个新的节点 v 的时候可以有两种情况：

1. 结点 u 通过树边到达结点 v，令：

low[u]=min(low[u],low[v])

1. 结点 u 通过反祖边到达结点 v，或者通过横叉边到达结点 v，此时v还在stack中，令：low[u]=min(low[u],dfn[v])

根据Tarjan算法对先前的图模拟一次。结点内的标号就是 dfn 值，结点边上的标号是表示 low 值，当前所在的结点用灰色表示。

 

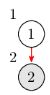
首先从第一个结点开始进行搜索，最初 low[1] = 1。此时栈里的结点是 1。

 

然后到达第二个结点，同时也初始化 low[2] = 2。此时栈里的结点是 1,2。

 

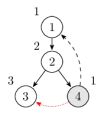
类似地，到达第三个结点，同时也初始化 low[3] = 3。此时栈里的结点是 1,2,3。此时结点 3 没有其余边可以继续进行搜索了，我们需要离开它了，因为发现 dfn[3] = low[3]，所以结点 3 是一个强连通分量的根，出栈直到结点 3 为止，得到刚好只有一个结点 3 的强连通分量。此时栈里的结点是 1,2。

 

从结点 3 返回后到结点 2，而后进入结点 4，从结点 4 可以到达结点 1，但是结点 1 已经访问过了，并且是通过反祖边，更新 low[4] 的值。此时栈里的结点是 1,2,4。

 

继续从结点 4 还可以通过横叉边到达结点 3，但是结点 3 并不在栈中（也就是结点 3 并没有路径到达结点 4），不做任何改动。此时栈里的结点是 1,2,4。

 

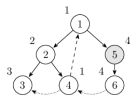
接着一直搜索直到结点 6。此时栈里的结点是 1,2,4,5,6。

 

从结点 6 出发可以通过横叉边到达结点 4，因为它已经访问过而且还在栈中，更新 low[6]。此时栈里的结点是 1,2,4,5,6。

 

接着回退到结点 5，使用结点 6 的值更新 low[5]。此时栈里的结点是 1,2,4,5,6。

 

从结点 5 出发经过结点 7 后到达结点 8。遇到反祖边回到结点 5 更新 low[8]。此时栈里的结点是 1,2,4,5,6,7,8。

 

继续到达结点 9。此时栈里的结点是 1,2,4,5,6,7,8,9。离开时发现 dfn[9] = low[9]。找到强连通分量，出栈。此时栈里的结点是 1,2,4,5,6,7,8。

 

回退到结点8，low[8]low[8]，且结点7到结点8是通过树边连接，所以low[7]=low[8]=5，继续回退，同理low[2]=low[4]=1。直到回到结点 1 的时候，low[1] = dfn[1]。此时栈里的结点是{1,2,4,5,6,7,8}即为所需的强连通分量。

Kaldi WFST中的最小化算法里也用到了类似Tarjan的算法。由于最小化过程中只是去掉“Dead State”，所以只要能达到终止状态的点都可以保留，所要保留的点数要比Tarjan算法的结果更大一些。Tarjan算法中要使连通分量重结点个数大于1，则要求有环的存在，否则连通分量中结点个数只会有一个，而最小化要求的是只要能从起始结点连通终止结点即可。两者看似没有太大联系，但是只要对Tarjan算法做略微改动，即可找到所有能连通起始状态和终止状态的结点。由于Tarjan算法基于深度优先遍历算法，在深度优先回溯的过程中即可标记某个状态是否可以到达终止状态；但是，假如图 7(b)中7号状态有一条到5号状态的边，那么在深度优先的过程中，7号状态有可能被标记为不能到达终止状态，但实际上7号状态通过5号状态是可以到达终止状态的。图中5号状态有到10号状态，2号状态和7号状态三条边，如果在深度优先的过程中最先到10号状态，那么7号状态便可正确的被标注为可以到达终止状态；如果深度优先的时候，最先遍历5号到7号状态的这一条边，那么7号状态便会被标记为不可以到达终止状态；此时如果将连通分量考虑进来，如果某个点可以到达终止状态，那么其所在的连通分量中的所有状态都可以到达终止状态，所以，7号状态就可以被正确的标记为可以到达终止状态。

经过变形的Tarjan强连通分量算法后，其结果如图 9所示，可以看到，原图中的状态7和状态9因为无法连通终止状态，已经被去除掉了。

 

图 9 连通图

逆运算

根据图 6伪代码中第11和12行可知，状态集会根据边“e”被分成多组，其中需要注意的是：o[e]是当前状态集“splitter”中的元素，i[e]是当前状态结点的输入边所对应的状态，由于WFST的数据结构中没有反向的指针，也就是说只能根据当前状态知道其前向的状态，而不能通过当前状态反推其后向状态，所以首先需要对图 9中的FST进行求逆运算，如图 10所示。根据图 9和图 10可以看出逆运算也就将所有的边反转即可，主要的操作就是引入了一个起始状态0，图 9中的终止状态8变成图 10中的状态9，在本文的例子中也可以直接将图 10中的状态9作为起始状态，而不用引入状态0。最主要的考虑是：如果某个FST具有多个不同的终止状态，那么这个时候就必须需要额外引入一个起始状态，所以，为了通用处理，对本文中的情况仍然引入额外的起始状态0；图 9其余状态值加1变成图 10中对应的状态。

 

图 10 逆运算

最小化

下面将以表格形成，详细演示Hopcroft算法的具体过程。由图 9可知，状态集合被分成了两部分：非终止状态集{0,1,2,3,4,5,6,7}和终止状态集{8}，初始时以终止状态集作为算法的Spliter。

0	P	{0,1,2,3,4,5,6,7} | {8}
	(i,o,w)
	W	{8}

以{8}作为Spliter，根据图 9和图 10可知，状态8有两种不同的反向边，一个是“3:3”类型的输入边，一种是“4:4”的边。首先处理“3:3”的边，可以知道{1,2,5,6}都可以通过“3:3”到达8号状态，而{0,3,4,7}则不能到达状态8，所以状态集{0,1,2,3,4,5,6,7}将被分割为{0,3,4,7}和{1,2,5,6}两个子集，由于两个子集中所含元素大小相同，所以可以把任意一个子集放入到W中，这里选择将{1,2,5,6}放到W中。

1	P	{0,3,4,7} | {8} | {1,2,5,6}
	(i,o,w)	{8;3:3}
	W	{8;4},{1,2,5,6}

处理“4:4”边的时候，会将状态集{0,3,4,7}分割为{0,4,7}和{3}，由于{3}中元素个数少，所以将{3}加入W(这里需要将个数少的子集加入队列，因为，需要求某个状态集的逆，所以状态集中的元素个数越少，时间越快)。这里W中的{3}既可以放在{1,2,5,6}的前面，也可以放在后面，根据实现时所使用的队列而异。

2	P	{0,4,7} | {8} | {1,2,5,6} | {3}
	(i,o,w)	{8;4:4}
	W	{3},{1,2,5,6}

处理状态集{3}，由于3的输入边中只有状态1和状态6以“1:1”边的方式指向{3}，所以状态集{1,2,5,6}被分为{1,6}和{2,5}两个子集。同时W中的{1,2,5,6}也被分为了{1,6}和{2,5}。

3	P	{0,4,7} | {8} | {2,5} | {3} | {1,6}
	(i,o,w)	{3;1:1}
	W	{1,6},{2,5}

处理状态子集{1,6}，首先处理“1:1”边，不会分割任意一个子集。

4	P	{0,4,7} | {8} | {2,5} | {3} | {1,6}
	(i,o,w)	{1,6;1:1}
	W	{1,6;2:2},{2,5}

处理边“2:2”时，也不会分割任意一个子集。

5	P	{0,4,7} | {8} | {2,5} | {3} | {1,6}
	(i,o,w)	{1,6;2:2}
	W	{2,5}

处理状态子集{2,5}，也需要处理“1:1”和“2:2”的情况，其结果如下。

6	P	{0,4,7} | {8} | {5} | {3} | {1,6} | {2}
	(i,o,w)	{2,5;1:1}
	W	{2;2:2}

当{2,5}被分割为{2}和{5}时，由于状态{5}只有“1:1”的输入边，而状态{2}还有“2:2”的边需要处理，所以W中的{2,5}被分割为{2;2:2}，处理完“2；2:2”边后结果如下。

7	P	{0,4} | {8} | {5} | {3} | {1,6} | {2} | {7}
	(i,o,w)	{2;2:2}
	W	{7}

将状态子集{7}作为spliter是，可以得到如下的结果。

8	P	{0,4} | {8} | {5} | {3} | {1} | {2} | {7} | {6}
	(i,o,w)	{7;2:2}
	W	{6}

将状态子集{6}作为spliter是，可以得到如下的结果。

9	P	{0} | {8} | {5} | {3} | {1} | {2} | {7} | {6} | {4}
	(i,o,w)	{6;1:1}
	W	{4}

将状态子集{4}作为spliter是，结果将不会发生变化。

10	P	{0} | {8} | {5} | {3} | {1} | {2} | {7} | {6} | {4}
	(i,o,w)	{4;2:2}
	W

至此，W中的所有状态子集都处理完成，最小化过程结束。

状态合并

经过最小化算法运算之后，会得到一系列的状态子集，有的状态子集中可能只有唯一的一个状态，有的状态子集中可能有多个状态，上面的例子得到的所有状态子集中都只有一个状态。假设在最小化的过程中没有经过连通分量运算，其他算法仍然不变，图 9(a)中7号和9号状态将会成为等价的状态子集，所以，最终只需要将7号状态和9号状态合并为1个状态即可。 

解码

解码时需要将编码中修改的两个地方进行恢复：第一、恢复状态1、2、3、5、6的终止状态属性；第二是恢复各状态边上的输入输出和权重值。最小化最终的结果如图 11所示。

图 11 Hopcroft算法结果