南瓜书《动手机器学习公益训练营》-卷积神经网络基础与LeNet

1 卷积神经网络基础

二维互相关运算

二维互相关（cross-correlation）运算的输入是一个二维输入数组和一个二维核（kernel）数组，输出也是一个二维数组，其中核数组通常称为卷积核或过滤器（filter）。卷积核的尺寸通常小于输入数组，卷积核在输入数组上滑动，在每个位置上，卷积核与该位置处的输入子数组按元素相乘并求和，得到输出数组中相应位置的元素。图1展示了一个互相关运算的例子，阴影部分分别是输入的第一个计算区域、核数组以及对应的输出。

二维卷积层

二维卷积层将输入和卷积核做互相关运算，并加上一个标量偏置来得到输出。卷积层的模型参数包括卷积核和标量偏置。

class Conv2D(nn.Module):
    def __init__(self, kernel_size):
        super(Conv2D, self).__init__()
        self.weight = nn.Parameter(torch.randn(kernel_size))
        self.bias = nn.Parameter(torch.randn(1))

    def forward(self, x):
        return corr2d(x, self.weight) + self.bias

特征图与感受野

二维卷积层输出的二维数组可以看作是输入在空间维度（宽和高）上某一级的表征，也叫特征图（feature map）。影响元素$x$的前向计算的所有可能输入区域（可能大于输入的实际尺寸）叫做$x$的感受野（receptive field）。

以图1为例，输入中阴影部分的四个元素是输出中阴影部分元素的感受野。我们将图中形状为$2\times 2$的输出记为$Y$，将$Y$与另一个形状为$2\times 2$的核数组做互相关运算，输出单个元素$z$。那么，$z$在$Y$上的感受野包括$Y$的全部四个元素，在输入上的感受野包括其中全部9个元素。可见，我们可以通过更深的卷积神经网络使特征图中单个元素的感受野变得更加广阔，从而捕捉输入上更大尺寸的特征。

填充和步幅

我们介绍卷积层的两个超参数，即填充和步幅，它们可以对给定形状的输入和卷积核改变输出形状。

填充

填充（padding）是指在输入高和宽的两侧填充元素（通常是0元素），图2里我们在原输入高和宽的两侧分别添加了值为0的元素。

图2 在输入的高和宽两侧分别填充了0元素的二维互相关计算

如果原输入的高和宽是$n_h$和$n_w$，卷积核的高和宽是$k_h$和$k_w$，在高的两侧一共填充$p_h$行，在宽的两侧一共填充$p_w$列，则输出形状为：

$$

(n_h+p_h-k_h+1)\times(n_w+p_w-k_w+1)

$$

我们在卷积神经网络中使用奇数高宽的核，比如$3\times 3$，$5\times 5$的卷积核，对于高度（或宽度）为大小为$2k+1$的核，令步幅为1，在高（或宽）两侧选择大小为$k$的填充，便可保持输入与输出尺寸相同。

步幅

在互相关运算中，卷积核在输入数组上滑动，每次滑动的行数与列数即是步幅（stride）。此前我们使用的步幅都是1，图3展示了在高上步幅为3、在宽上步幅为2的二维互相关运算。

图3 高和宽上步幅分别为3和2的二维互相关运算

一般来说，当高上步幅为$s_h$，宽上步幅为$s_w$时，输出形状为：

$$

\lfloor(n_h+p_h-k_h+s_h)/s_h\rfloor \times \lfloor(n_w+p_w-k_w+s_w)/s_w\rfloor

$$

如果$p_h=k_h-1$，$p_w=k_w-1$，那么输出形状将简化为$\lfloor (n_h+s_h-1)/s_h\rfloor \times \lfloor (n_w+s_w-1)/s_w\rfloor$。更进一步，如果输入的高和宽能分别被高和宽上的步幅整除，那么输出形状将是$(n_h/s_h)\times (n_w/s_w)$。

当$p_h=p_w=p$时，我们称填充为$p$；当$s_h=s_w=s$时，我们称步幅为$s$。

多输入通道和多输出通道

之前的输入和输出都是二维数组，但真实数据的维度经常更高。例如，彩色图像在高和宽2个维度外还有RGB（红、绿、蓝）3个颜色通道。假设彩色图像的高和宽分别是$h$和$w$（像素），那么它可以表示为一个$3\times h\times w$的多维数组，我们将大小为3的这一维称为通道（channel）维。

多输入通道

卷积层的输入可以包含多个通道，图4展示了一个含2个输入通道的二维互相关计算的例子。

图4 含2个输入通道的互相关计算

假设输入数据的通道数为$c_i$，卷积核形状为$k_h\times k_w$，我们为每个输入通道各分配一个形状为$k_h\times k_w$的核数组，将$c_i$个互相关运算的二维输出按通道相加，得到一个二维数组作为输出。我们把$c_i$个核数组在通道维上连结，即得到一个形状为$c_i\times k_h\times k_w$的卷积核。

多输出通道

卷积层的输出也可以包含多个通道，设卷积核输入通道数和输出通道数分别为$c_i$和$c_o$，高和宽分别为$k_h$和$k_w$。如果希望得到含多个通道的输出，我们可以为每个输出通道分别创建形状为$c_i\times k_h\times k_w$的核数组，将它们在输出通道维上连结，卷积核的形状即$c_o\times c_i\times k_h\times k_w$。

对于输出通道的卷积核，我们提供这样一种理解，一个$c_i\times k_h\times k_w$的核数组可以提取某种局部特征，但是输入可能具有相当丰富的特征，我们需要有多个这样的$c_i\times k_h\times k_w$的核数组，不同的核数组提取的是不同的特征。

1x1卷积层

最后讨论形状为$1\times 1$的卷积核，我们通常称这样的卷积运算为$1\times 1$卷积，称包含这种卷积核的卷积层为$1\times 1$卷积层。图5展示了使用输入通道数为3、输出通道数为2的$1\times 1$卷积核的互相关计算。

图5 1x1卷积核的互相关计算。输入和输出具有相同的高和宽

$1\times 1$卷积核可在不改变高宽的情况下，调整通道数。$1\times 1$卷积核不识别高和宽维度上相邻元素构成的模式，其主要计算发生在通道维上。假设我们将通道维当作特征维，将高和宽维度上的元素当成数据样本，那么$1\times 1$卷积层的作用与全连接层等价。

卷积层与全连接层的对比

二维卷积层经常用于处理图像，与此前的全连接层相比，它主要有两个优势：

一是全连接层把图像展平成一个向量，在输入图像上相邻的元素可能因为展平操作不再相邻，网络难以捕捉局部信息。而卷积层的设计，天然地具有提取局部信息的能力。

二是卷积层的参数量更少。不考虑偏置的情况下，一个形状为$(c_i,c_o,h,w)$的卷积核的参数量是$c_i\times c_o\times h\times w$，与输入图像的宽高无关。假如一个卷积层的输入和输出形状分别是$(c_1,h_1,w_1)$和$(c_2,h_2,w_2)$，如果要用全连接层进行连接，参数数量就是$c_1\times c_2\times h_1\times w_1\times h_2\times w_2$。使用卷积层可以以较少的参数数量来处理更大的图像。

卷积层的简洁实现

我们使用Pytorch中的nn.Conv2d类来实现二维卷积层，主要关注以下几个构造函数参数：

• in_channels (python:int) – Number of channels in the input imag
• out_channels (python:int) – Number of channels produced by the convolution
• kernel_size (python:int or tuple) – Size of the convolving kernel
• stride (python:int or tuple, optional) – Stride of the convolution. Default: 1
• padding (python:int or tuple, optional) – Zero-padding added to both sides of the input. Default: 0
• bias (bool, optional) – If True, adds a learnable bias to the output. Default: True

forward函数的参数为一个四维张量，形状为$(N,C_{in},H_{in},W_{in})$，返回值也是一个四维张量，形状为$(N,C_{out},H_{out},W_{out})$，其中$N$是批量大小，$C,H,W$分别表示通道数、高度、宽度。

池化

二维池化层

池化层主要用于缓解卷积层对位置的过度敏感性。同卷积层一样，池化层每次对输入数据的一个固定形状窗口（又称池化窗口）中的元素计算输出，池化层直接计算池化窗口内元素的最大值或者平均值，该运算也分别叫做最大池化或平均池化。图6展示了池化窗口形状为$2\times 2$的最大池化。

图6 池化窗口形状为 2 x 2 的最大池化

二维平均池化的工作原理与二维最大池化类似，但将最大运算符替换成平均运算符。池化窗口形状为$p\times q$的池化层称为$p\times q$池化层，其中的池化运算叫作$p\times q$池化。

池化层也可以在输入的高和宽两侧填充并调整窗口的移动步幅来改变输出形状。池化层填充和步幅与卷积层填充和步幅的工作机制一样。

在处理多通道输入数据时，池化层对每个输入通道分别池化，但不会像卷积层那样将各通道的结果按通道相加。这意味着池化层的输出通道数与输入通道数相等。

池化层的简洁实现

我们使用Pytorch中的nn.MaxPool2d实现最大池化层，关注以下构造函数参数：

• kernel_size – the size of the window to take a max over
• stride – the stride of the window. Default value is kernel_size
• padding – implicit zero padding to be added on both sides

forward函数的参数为一个四维张量，形状为$(N,C,H_{in},W_{in})$，返回值也是一个四维张量，形状为$(N,C,H_{out},W_{out})$，其中$N$是批量大小，$C,H,W$分别表示通道数、高度、宽度。

课后练习题

本次练习真的是大型翻车现场，以为自己理解了内容，不加思考就下意识做题，果然翻车

题目中彩色（RGB）图像，告知了图像是3通道的，所以全连接的输入 应该是$$3\times 256\times 256$$ ,对应1000个输出单元，所以再乘以1000，为权重参数个数，1000个输出单元每一个包含一个偏执项，所以再加1000 。

输入的是彩色RGB图像，所以输入数据有3通道，卷积核为$$3\times 3$$,输出10通道，所以卷积层的参数：$$3\times 3\times 3(输入数据的通道数)\times 10(输出数据通道数)+10（每个输出通道1个偏置项）$$

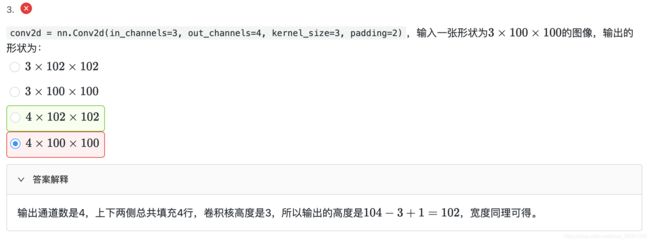
padding=2 表示上下左右填充均为2，所以w = 104 h=104

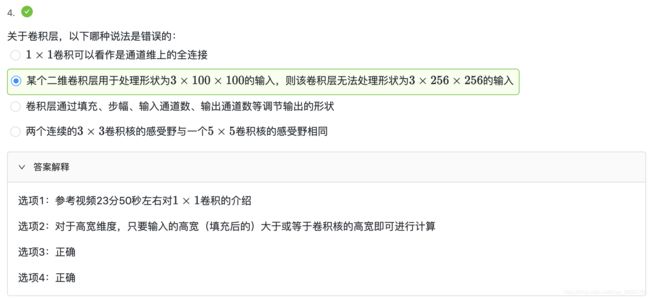
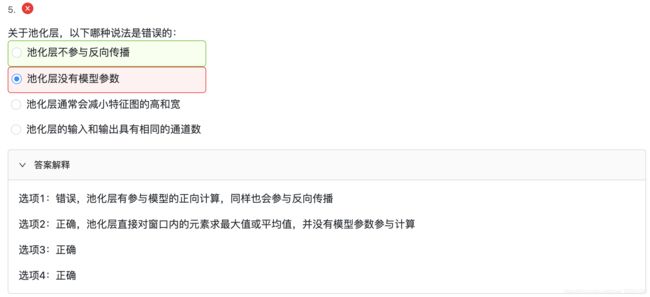
2 LeNet 模型

1. lenet 模型介绍
2. lenet 网络搭建
3. 运用lenet进行图像识别-fashion-mnist数据集

Convolutional Neural Networks

使用全连接层的局限性：

• 图像在同一列邻近的像素在这个向量中可能相距较远。它们构成的模式可能难以被模型识别。
• 对于大尺寸的输入图像，使用全连接层容易导致模型过大。

使用卷积层的优势：

• 卷积层保留输入形状。
• 卷积层通过滑动窗口将同一卷积核与不同位置的输入重复计算，从而避免参数尺寸过大。

LeNet 模型

LeNet分为卷积层块和全连接层块两个部分。下面我们分别介绍这两个模块。

卷积层块里的基本单位是卷积层后接平均池化层：卷积层用来识别图像里的空间模式，如线条和物体局部，之后的平均池化层则用来降低卷积层对位置的敏感性。

卷积层块由两个这样的基本单位重复堆叠构成。在卷积层块中，每个卷积层都使用$5\times 5$的窗口，并在输出上使用sigmoid激活函数。第一个卷积层输出通道数为6，第二个卷积层输出通道数则增加到16。

全连接层块含3个全连接层。它们的输出个数分别是120、84和10，其中10为输出的类别个数。

下面我们通过Sequential类来实现LeNet模型。

#import
import sys
sys.path.append("/home/kesci/input")
import d2lzh1981 as d2l
import torch
import torch.nn as nn
import torch.optim as optim
import time

#net
class Flatten(torch.nn.Module):  #展平操作
    def forward(self, x):
        return x.view(x.shape[0], -1)

class Reshape(torch.nn.Module): #将图像大小重定型
    def forward(self, x):
        return x.view(-1,1,28,28)      #(B x C x H x W)
    
net = torch.nn.Sequential(     #Lelet                                                  
    Reshape(),
    nn.Conv2d(in_channels=1, out_channels=6, kernel_size=5, padding=2), #b*1*28*28  =>b*6*28*28
    nn.Sigmoid(),                                                       
    nn.AvgPool2d(kernel_size=2, stride=2),                              #b*6*28*28  =>b*6*14*14
    nn.Conv2d(in_channels=6, out_channels=16, kernel_size=5),           #b*6*14*14  =>b*16*10*10
    nn.Sigmoid(),
    nn.AvgPool2d(kernel_size=2, stride=2),                              #b*16*10*10  => b*16*5*5
    Flatten(),                                                          #b*16*5*5   => b*400
    nn.Linear(in_features=16*5*5, out_features=120),
    nn.Sigmoid(),
    nn.Linear(120, 84),
    nn.Sigmoid(),
    nn.Linear(84, 10)
)

#接下来我们构造一个高和宽均为28的单通道数据样本，并逐层进行前向计算来查看每个层的输出形状。print
X = torch.randn(size=(1,1,28,28), dtype = torch.float32)
for layer in net:
    X = layer(X)
    print(layer.__class__.__name__,'output shape: \t',X.shape)

可以看到，在卷积层块中输入的高和宽在逐层减小。卷积层由于使用高和宽均为5的卷积核，从而将高和宽分别减小4，而池化层则将高和宽减半，但通道数则从1增加到16。全连接层则逐层减少输出个数，直到变成图像的类别数10。

获取数据和训练模型

# 数据
batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(
    batch_size=batch_size, root='/home/kesci/input/FashionMNIST2065')
print(len(train_iter))

#数据展示
import matplotlib.pyplot as plt
def show_fashion_mnist(images, labels):
    d2l.use_svg_display()
    # 这里的_表示我们忽略（不使用）的变量
    _, figs = plt.subplots(1, len(images), figsize=(12, 12))
    for f, img, lbl in zip(figs, images, labels):
        f.imshow(img.view((28, 28)).numpy())
        f.set_title(lbl)
        f.axes.get_xaxis().set_visible(False)
        f.axes.get_yaxis().set_visible(False)
    plt.show()

for Xdata,ylabel in train_iter:
    break
X, y = [], []
for i in range(10):
    print(Xdata[i].shape,ylabel[i].numpy())
    X.append(Xdata[i]) # 将第i个feature加到X中
    y.append(ylabel[i].numpy()) # 将第i个label加到y中
show_fashion_mnist(X, y)

# This function has been saved in the d2l package for future use
#use GPU
def try_gpu():
    """If GPU is available, return torch.device as cuda:0; else return torch.device as cpu."""
    if torch.cuda.is_available():
        device = torch.device('cuda:0')
    else:
        device = torch.device('cpu')
    return device

device = try_gpu()
device

我们实现evaluate_accuracy函数，该函数用于计算模型net在数据集data_iter上的准确率。

#计算准确率
'''
(1). net.train()
  启用 BatchNormalization 和 Dropout，将BatchNormalization和Dropout置为True
(2). net.eval()
不启用 BatchNormalization 和 Dropout，将BatchNormalization和Dropout置为False
'''

def evaluate_accuracy(data_iter, net,device=torch.device('cpu')):
    """Evaluate accuracy of a model on the given data set."""
    acc_sum,n = torch.tensor([0],dtype=torch.float32,device=device),0
    for X,y in data_iter:
        # If device is the GPU, copy the data to the GPU.
        X,y = X.to(device),y.to(device)
        net.eval()
        with torch.no_grad():
            y = y.long()
            acc_sum += torch.sum((torch.argmax(net(X), dim=1) == y))  #[[0.2 ,0.4 ,0.5 ,0.6 ,0.8] ,[ 0.1,0.2 ,0.4 ,0.3 ,0.1]] => [ 4 , 2 ]
            n += y.shape[0]
    return acc_sum.item()/n

训练模型

#训练函数
def train_ch5(net, train_iter, test_iter,criterion, num_epochs, batch_size, device,lr=None):
    """Train and evaluate a model with CPU or GPU."""
    print('training on', device)
    net.to(device)
    optimizer = optim.SGD(net.parameters(), lr=lr)
    for epoch in range(num_epochs):
        train_l_sum = torch.tensor([0.0],dtype=torch.float32,device=device)
        train_acc_sum = torch.tensor([0.0],dtype=torch.float32,device=device)
        n, start = 0, time.time()
        for X, y in train_iter:
            net.train()
            
            optimizer.zero_grad()
            X,y = X.to(device),y.to(device) 
            y_hat = net(X)
            loss = criterion(y_hat, y)
            loss.backward()
            optimizer.step()
            
            with torch.no_grad():
                y = y.long()
                train_l_sum += loss.float()
                train_acc_sum += (torch.sum((torch.argmax(y_hat, dim=1) == y))).float()
                n += y.shape[0]
        test_acc = evaluate_accuracy(test_iter, net,device)
        print('epoch %d, loss %.4f, train acc %.3f, test acc %.3f, '
              'time %.1f sec'
              % (epoch + 1, train_l_sum/n, train_acc_sum/n, test_acc,
                 time.time() - start))

我们重新将模型参数初始化到对应的设备device(cpu or cuda:0)之上，并使用Xavier随机初始化。损失函数和训练算法则依然使用交叉熵损失函数和小批量随机梯度下降。

# 训练
lr, num_epochs = 0.9, 10

def init_weights(m):
    if type(m) == nn.Linear or type(m) == nn.Conv2d:
        torch.nn.init.xavier_uniform_(m.weight)

net.apply(init_weights)
net = net.to(device)

criterion = nn.CrossEntropyLoss()   #交叉熵描述了两个概率分布之间的距离，交叉熵越小说明两者之间越接近
train_ch5(net, train_iter, test_iter, criterion,num_epochs, batch_size,device, lr)

# test
for testdata,testlabe in test_iter:
    testdata,testlabe = testdata.to(device),testlabe.to(device)
    break
print(testdata.shape,testlabe.shape)
net.eval()
y_pre = net(testdata)
print(torch.argmax(y_pre,dim=1)[:10])
print(testlabe[:10])

课后练习题