cs231n-Lecture5

CS231N–神经网络训练

一、作业讲解

• Assignment2：CNN训练作业，预训练与细调，CNN先在ImageNet进行大量数据训练，在在小批量数据中进行训练。

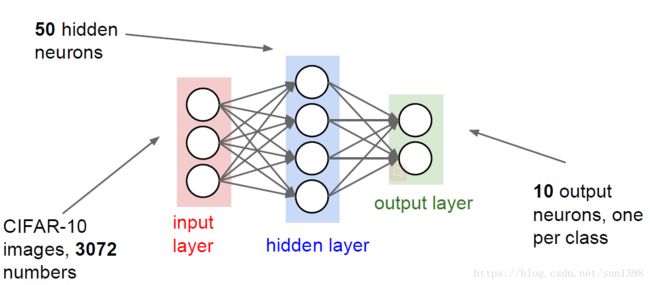
1. CNN的迁移学习

• 可以先使用CNN在比如ImageNet这样的大数据集上先进行预训练，熟练好权重和超参数，去掉最上方的分类层，看成是一个固定特征提取器

• 自己的数据量较少的时候可以仅仅替换最后的分类层；如果有中等规模的数据，可以再细调几层的反向传播层。

• 已经有人在ImageNet各种数据上进行与训练模型，caffe model zoo，设置好大量超参数

• 电脑的计算资源是有限的，要权衡时间与效果

2. CNN发展的历史：

(1)1957年弗兰克-罗森布拉特制作了感知机：硬件实现的、电路电子元件实现的字母识别；激活函数使用的是二阶阶梯函数，没有微分；更新函数通过设置权值来得到比较满意的结果；没有损失函数，也没有反向传播。

(2)1960年多层次感知机：依旧硬件实现；依旧没有反向传播，但是通过学习规则改变来观察是否得到更好结果；程序设计的观念升级，巨大的改变。

(3)1980年鲁姆哈特第一次提出了损失函数、反向传播、梯度下降的概念，当时反向传播训练效果并不好

(4)2006年辛顿Reinvigorated research in Deep Learning：10层无监督学习网络，一层层训练，然后集合在一起，整合起来进行反向传播。

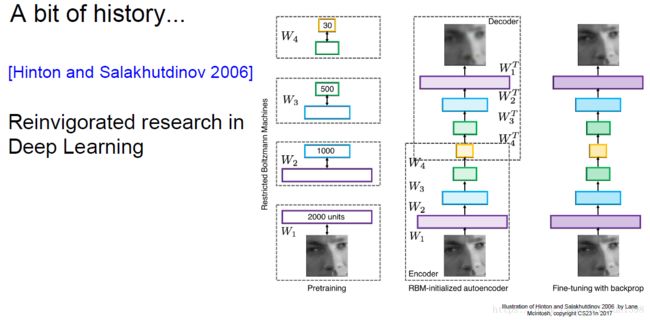
• 不使用预训练的方法是可以行的，但是一定要注意初始化函数的选用
• 这里使用的Sigmoid激活函数，但并不是合适的，后续会将激活函数的特点
• 2006年也有其他很多研究，深度学习这个词也是这一年流传，神经网络的变种。

(5)2010年-2012年语音识别的领域，神经网络比传统特征提取更加有效果；2012年在机器视觉比赛方面，AlexNex远远强于其他算法

- 原因在于找到了对激活函数进行初始化的方法；GPU的出现导致的算力提升；互联网时代数据量的提升。

二、激活函数

- 激活函数是用来使得各层神经网络之间不是线性，不然多层神经网络将不起作用

1. sigmoid函数

σ(x)=1/(1+e−x)σ′(x)=(1−σ(x))σ(x) σ ( x ) = 1 / ( 1 + e − x ) σ ′ ( x ) = ( 1 − σ ( x ) ) σ ( x )

• 由于模拟了神经元饱和的情况，取值在[0,1]，是历史上最常用的激活函数。
• 缺点1：饱和神经元，在函数的两边梯度为0，出现梯度消失。只有在sigmoid的激活区，训练才能正常进行下去。

• 缺点2：sigmoid函数不是中心对称，数据预处理过程总会希望是中心对称的；sigmoid的取值落在0,1之间，经过第一层后，每层 xi x i 值都是正值，将会导致每梯度值总会是一个方向的正值，这样计算得到的每一层的梯度值都是一个方向，优化只会朝着一个方向逼近，优化走阶梯方向，收敛速度慢。
  

  f(∑iwixi+b) f ( ∑ i w i x i + b )

• 缺点3：exp()计算成本高、时间长

2. tanh函数

tanh(x)=21+e−2x−1tanh′(x)=1−tanh(x)2 tanh ⁡ ( x ) = 2 1 + e − 2 x − 1 tanh ′ ⁡ ( x ) = 1 − tanh ⁡ ( x ) 2

• tanh相当于一个对称的sigmoid函数，是中心对称的，因此收敛效果比sigmoid好
• 缺点1：依旧是饱和神经元，在两边梯度为0时，依旧会出现梯度消失的现象。
• 缺点2：exp的计算依然耗费大量时间。

3. ReLU

max(x,0)={0forx<0xforx≥0max′(x)={0forx<01forx≥0 max ( x , 0 ) = { 0 f o r x < 0 x f o r x ≥ 0 max ′ ( x ) = { 0 f o r x < 0 1 f o r x ≥ 0

• ReLU是线性非饱和函数，对SGD的加速效果非常明显，Alex Krizhevsky 指出有 6 倍之多。
• ReLU只需要一个阈值就能够得到激活值，计算成本低。
• 正值的梯度值为1，只要学习率合适，那么对于优化的加速效果就会比较明显，上面的函数在两端时，梯度值下降严重，可能这就是快的原因。
• 缺点1：在小于0的值，梯度也为0，将没有激活作用。
• 缺点2：ReLU的神经元比较脆弱，训练过程中容易死掉：在初始化时神经元没有被激活；梯度值较大经过ReLU神经元，学习率太高导致训练中落入死去，导致数据多样化丢失，更新参数后，后续梯度为0.
• 训练方法：在进行一轮训练后，对梯度值进行检测，如果发现10%到20%的梯度死亡，那么就是学习率设置的太高

4. LeakyReLU & PReLU

f(x)={0.01xforx<0xforx≥0f′(x)={0.01forx<01forx≥0 f ( x ) = { 0 .01 x f o r x < 0 x f o r x ≥ 0 f ′ ( x ) = { 0.01 f o r x < 0 1 f o r x ≥ 0

• 在负值时，给予-0.01的梯度，用来解决ReLU神经元死亡问题，但有时也并不一定会起作用
• 当然不一定是0.01，可以是一个参数 αx α x 形成一个超参数。

5. Exponential Linear Units(ELU)

f(x)={α(e(x)−1)forx<0x forx≥0f′(x)={αe(x)forx<01forx≥0 f ( x ) = { α ( e ( x ) − 1 ) f o r x < 0 x   f o r x ≥ 0 f ′ ( x ) = { α e ( x ) f o r x < 0 1 f o r x ≥ 0

• ELU是一个0均值的函数，效果会好一些，但实际上ReLU已经够用。纯属锦上添花，可能是用来发论文的，实际上属于学术上走偏的感觉。

6. Maxout

max(wT1x+b1,wT2x+b1) max ( w 1 T x + b 1 , w 2 T x + b 1 )

• 与众不同的函数，改变了计算的变量和计算方式，使用两组参数进行计算，形成两个超平面，求其中的最大值进行计算，求导是最大值那组参数进行梯度更新，不断缩最后的损失函数。
• 非线性激活函数，仍然具有分段性和高效性
• ReLU和Leaky ReLU的一般形式，没有ReLU的缺点，神经元不会失活死掉。
• 有两组参数值，两倍参数可能觉得方法并不理想，ReLU依然是使用最广泛的。

三、数据预处理

1. Step1:数据预处理

• PCA算法（主成分分析算法）：通过协方差矩阵可以求得特征向量U，然后把每个数据点，投影到这两个新的特征向量所在空间平面，把协方差矩阵变成对角矩阵；用于数据的降维。
• Whiteniing算法：白化算法将协方差矩阵变成单位矩阵，用于使得数据在每一个维度都变得均匀。
• 过去的图像处理、机器学习中很常用，但是在深度学习中必要性降低。
• PCA需要求取一个非常大的协方差矩阵，通常进行局部白化，在图像中加入一个白化过滤器，现在也不是很常用。

2. 均值中心化

• 对一幅图像求取均值，图像的每个像素点减去均值图像
• 在每个颜色通道上分别计算每个通道的颜色均值，然后通过减去每个通道的均值来进行去中心化
• 在深度学习中，使用这样的方法就足够，不需要过多的数据预处理，比如PCA和白化。

四、权重初始化–很重要

1. 初始化的重要性

(1) 假设权值为0，初始化10层网络，这样网络对称，那么每一层都是相同的，梯度值也相同，这样网络就无法得到训练。

(2) 方法1：小数字随机初始化，均值为0，标准差为1e-2的高斯分布。

W=0.01∗np.random.randn(D,H) W = 0.01 ∗ n p . r a n d o m . r a n d n ( D , H )

• 对于层数较少时是适用的，但是当层数较多时，那么高斯分布的参数，假如有10层，每层的值进行权重乘法以后，后续数值将乘以0.01，这样经过多层以后权重的分布就再也无法保持均值为0，标准差为1e-2的高斯分布。后续分布均值为0,标准差成指数下降，这样在后期只会分布在0上，多层以后输入为0，反向传播过程中求取的梯度值将会非常小，这样在反向传播中，每一层后最后梯度趋于0，这就是梯度消失现象。
  

(3) 方法1，使用1来代替0.01进行随机初始化
- 对于tanh函数就会出现结果分布在两端-1和1，处于饱和区，后续计算所有神经元都饱和，梯度为0，损失函数将不会变，无法进行反向传播，没有权值得到更新。

(4) Reaseonable初始化：使得神经元输出的方差为1。

W=np.random.randn(fan_in,fan_out)/np.sqrt(fan_in) W = n p . r a n d o m . r a n d n ( f a n _ i n , f a n _ o u t ) / n p . s q r t ( f a n _ i n )

• 对于处于神经网络前面层的让权重输出在合适的范围，后续每层的权重都略有增大，可以有一个在预期中的范围，不饱和也不趋于0，这个方法能够在tanh中得到使用

• 但是对于ReLU的情况，加权计算将失败，ReLU是半边函数,将方差的权重缩小了一半，因此要给他补上一个2。

W=np.random.randn(fan_in,fan_out)/np.sqrt(fan_in/2) W = n p . r a n d o m . r a n d n ( f a n _ i n , f a n _ o u t ) / n p . s q r t ( f a n _ i n / 2 )

2. 这些都是策略性的内容，可以使得深度学习走的更远的原因

五、Batch Normalization（批归一）

x^(k)=x(k)−E[x(k)]Var[x(k)]−−−−−−−−√ x ^ ( k ) = x ( k ) − E [ x ( k ) ] V a r [ x ( k ) ]

1. BN的意义

• 随机梯度下降法（SGD）对于训练深度网络简单高效，但人为的去选择参数，比如学习率、参数初始化、权重衰减系数、Drop out比例等。这些参数的选择对训练结果至关重要，以至于我们很多时间都浪费在这些的调参上。那么使用BN（详见论文《Batch Normalization_ Accelerating Deep Network Training by Reducing Internal Covariate Shift》）之后，你可以不需要那么刻意的慢慢调整参数。

• 在训练的过程中，每一层的激活函数后的输出将会作为后一层的输入，这样当神经网络进行训练后，前级输出极大地影响后续的结果，而进行BN后，归一化的结果将降低前级对后级的影响

2. BN的原理

• 对于N个图像的D维特征，每一层进行均值和方差计算，这样保证每一个特征都满足高斯标准化。

• BN插入在激活函数前，这样讲权重乘法后的输入归一到均值为0，方差为1，这样经过激活函数后的输出的数据分布依然保持均匀性。

3. BN的参数调节

y(k)=γ(k)x^(k)+β^(k)γ(k)=Var[x(k)]−−−−−−−−√β^=E[x(k)] y ( k ) = γ ( k ) x ^ ( k ) + β ^ ( k ) γ ( k ) = V a r [ x ( k ) ] β ^ = E [ x ( k ) ]

• 神经网络学习到的数据本身就是在分布在激活函数两侧，那么归一将会打断前后层的之间的关系，因此引入变换重构，可学习参数γ、β。

• 同时当 γ(k)=Var[x(k)]−−−−−−−−√ γ ( k ) = V a r [ x ( k ) ] 、 β^=E[x(k)] β ^ = E [ x ( k ) ] 时，相当于取消BN算法。因此当发现BN能够使得网络优化效果增强，可以采用BN算法调节，反之则通过参数取消BN算法。

• 实际上不是对于每一个特征都拥有一个γ、β，而是对于每一层的特征图，使用参数共享的方式，只有

4. BN的优点

• 优化流向网络中的梯度，支持更高的学习率，能够快速训练模型。
• 由于使用了归一化的方法，使得每层结果趋向于均值0，方差1，解决梯度消失问题；降低对于合理初始化的依赖性，可以更加随机的使用初始化值
• 改善正则化策略：作为正则化的一种形式，减少对于dropout的依赖。
• 可以将训练数据打乱，经过归一化后将会增强统一性，能够提高1%的精度。
• 在测试时，均值和方差不基于小批量进行计算，可以使用训练过程中的计算得到值的均值。

六、跟踪训练过程

1. 预处理数据

2. 选择合适的网络结构

3. 迭代输出损失函数和准确率

• 检查损失函数：将正则化参数调大1e3，与无正则化相比，观察损失函数是否增大，增大即是合理的
• 小批量数据进行训练：关闭正则化，观察损失函数将下降，准确率应该逼近100%
• 小正则化参数、调节合适学习率：训练时发现损失函数下降很慢，准确率有增大，但是结果较差，属于学习率太低；损失函数出现NaN，表示学习率太高。

七、超参数优化

1. 交叉验证策略

• 将训练集划分为多个交叉验证集mini-batch，选择不同的参数作为集合，进行小批量参数验证。
• 使用较少的迭代次数来进行验证哪些参数是合适，损失函数下降快，准确率增大快。
• 精细化参数设置，长时间进行验证，选择到合适的参数。
• 探测到损失函数爆炸现象：损失函数增大为原来值的3倍，需要中断函数，减少时间浪费。
  
• 使用log空间阈值进行参数搜索
  
• 精细化搜索，调节空间域范围
  
• 随机搜素使得参数在空间份上更加均匀
  
• 监测并可视化准确率，分析哪些参数变动导致准确率变化，推测原因，修正超参数：网络层数；每层神经元数目；学习率、衰减率、更新模型；正则化。