CS231n-Lecture5:卷积神经网络（CNN / ConvNets）
卷积神经网络（CNN）
- 为什么要使用卷积？
- CNN的层
- 输入层（INPUT）
- 卷积层（CONV）
- 过滤器（卷积核）—— 特征提取器
- 权值共享
- 激活层（ReLU）
- 池化层 （POOL）—— 降采样
- 全连接层（FC）
- reference
为什么要使用卷积？
卷积的主要目的是为了从输入图像中提取特征。卷积可以通过从输入的一小块数据中学习到图像的特征，并且可以保留像素的空间关系。
CNN的层
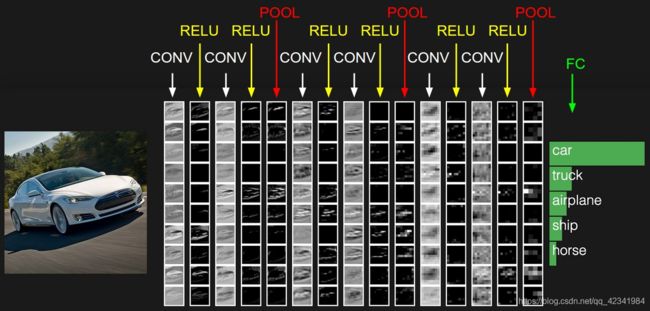
CNN将原始图像从原始像素值逐层转换为最终的类别分数。
CNN网络一共有5个层级结构：
- 输入层（INPUT）
- 卷积层（CONV）
- 激活层（ReLU）
- 池化层（POOL）
- 全连接层（FC）
最常见的ConvNet架构遵循以下模式：
INPUT -> [[CONV -> RELU]*N -> POOL?]*M -> [FC -> RELU]*K -> FC
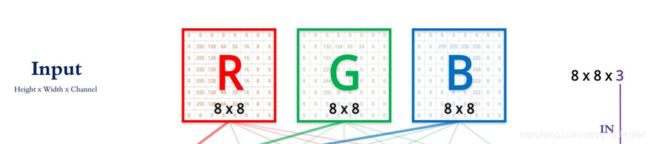
输入层（INPUT）
- 黑白图像： W × H × 1 W\times H\times 1 W×H×1
- 彩色图像： W × H × 3 W\times H\times 3 W×H×3（R，G，B三个通道）
卷积层（CONV）
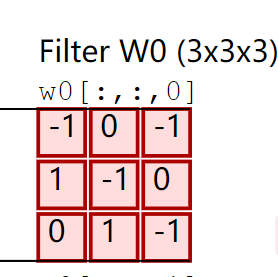
过滤器（卷积核）—— 特征提取器
局部感知：
和全连接层不同，卷积层的每个神经元仅连接到输入体的局部区域。区域的范围是一个称为神经元感受野的超参数（即滤波器的大小）。在卷积运算时，会给定一个大小为 F × F F\times F F×F的方阵，该矩阵的大小又称为感受野。过滤器的深度 d d d 和输入层的深度 d d d 维持一致，因此可得到大小为 F × F × d F\times F\times d F×F×d 的过滤器，又叫做卷积核。在实际的操作中，不同的模型会确定不同数量的过滤器（卷积核），其个数记为 K K K。
输入：
输入体大小： W 1 × H 1 × D 1 W_1 \times H_1 \times D_1 W1×H1×D1
超参数：
- 过滤器大小 - F F F
- 过滤器数量 - K K K
- 步幅（stride）- S S S
- 零填充量（zero-padding）- P P P
一定大小的输入体和一定大小的过滤器，再加上一些额外参数，会生成确定大小的输出体：
输出：
输出体大小： W 2 × H 2 × D 2 W_2 \times H_2 \times D_2 W2×H2×D2
则输出矩阵的大小计算公式为：
W 2 = ( W 1 − F + 2 P ) / S + 1 W_2=(W_1 - F + 2P)/S + 1 W2=(W1−F+2P)/S+1
H 2 = ( W 1 − F + 2 P ) / S + 1 H_2=(W_1- F + 2P)/S + 1 H2=(W1−F+2P)/S+1
D 2 = K D_2=K D2=K
举例说明：
W 1 = 5 , H 1 = 5 , D 1 = 3 W_1 = 5, H_1 = 5, D_1 = 3 W1=5,H1=5,D1=3
K = 2 , F = 3 , S = 2 , P = 1 K = 2, F = 3, S = 2, P = 1 K=2,F=3,S=2,P=1
卷积演示-demo
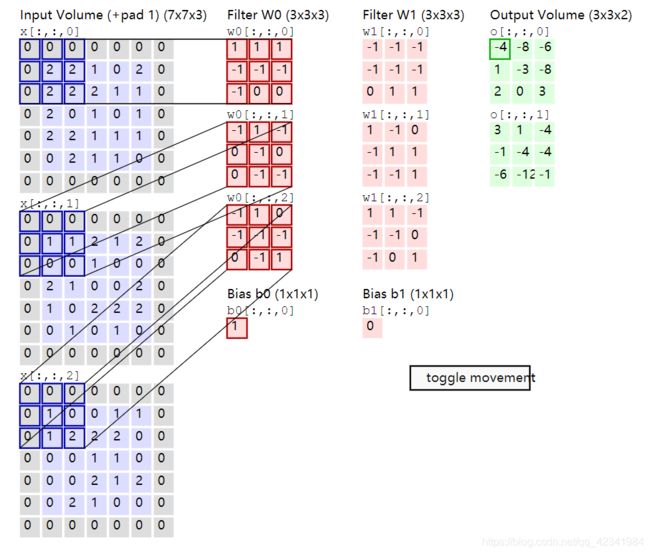
可以看到：
第一个卷积核 W 0 W_0 W0和输入体做卷积得到输出体的第一层，即Feature Map 0（ o [ : , : , 0 ] o[:,:,0] o[:,:,0]）；
第二个卷积核 W 1 W_1 W1和输入体做卷积得到输出体的第二层，即Feature Map 1（ o [ : , : , 1 ] o[:,:,1] o[:,:,1]）。
备注：输出的每一个Feature Map有3x3=9个神经元。
每一个卷积核滤波得到的图像就是一类特征的映射，即一个Feature Map。
在卷积神经网络中，一个卷积层可以有多个不同的卷积核（也可以说是滤波器），而每个卷积核在输入图像上滑动且每次只处理一小块图像。这样输入端的卷积层可以提取到图像中最基础的特征，比如不同方向的直线或者拐角；接着再组合成高阶特征，比如三角形、正方形等；再继续抽象组合，得到眼睛、鼻子和嘴等五官；最后再将五官组合成一张脸，完成匹配识别。即每个卷积层提取的特征，在后面的层中都会抽象组合成更高阶的特征。
权值共享
“卷积核”的权值共享只在每个单独通道上有效，即：对输入体的一个通道（即输入体的一个层），对应有一个卷积核的一个通道（层） 去滑动并计算和这个通道每一个部分的卷积。在这个输入体的一个通道中，我们可以说这个权值是共享的。但是，对应于输入体的其他通道，会有卷积核的其他通道（层）去做该通道的感受野特征提取。所以说通道与通道间的对应的卷积核的权值是独立不共享的。
举例说明：
如上图，卷积核 W 0 W_0 W0的通道0在输入体的通道0上要做9次滑动并做9次卷积运算，即在这9次运算过程中，权值是共享的 —— 均为卷积核 W 0 W_0 W0的通道0的那9个权值：
激活层（ReLU）
在神经网络中，对于图像，我们主要采用了卷积的方式来处理，也就是对每个像素点赋予一个权值，这个操作显然就是线性的。但是对于我们样本来说，不一定是线性可分的，为了解决这个问题，我们可以进行线性变化，或者我们引入非线性因素，解决线性模型所不能解决的问题。
激活层实际上是对卷积层的输出结果做一次非线性映射，基本上都是采用了ReLU函数。
池化层 （POOL）—— 降采样
在连续的Conv层之间定期插入一个Pooling层。对输入的特征图进行压缩，逐渐减小表示的空间大小，以减少网络中的参数和计算量，从而也控制过拟合：
- 一方面使特征图变小，简化网络计算复杂度；
- 一方面进行特征压缩，提取主要特征
一般有两种方法：
- Max Pooling：最大池化
- Average Pooling：平均池化
和卷积层类似：
输入：
输入体大小： W 1 × H 1 × D 1 W_1 \times H_1 \times D_1 W1×H1×D1
超参数：
- 过滤器大小 - F F F
- 步幅（stride）- S S S
对于池化层，通常不使用零填充来填充输入。
输出：
输出体大小： W 2 × H 2 × D 2 W_2 \times H_2 \times D_2 W2×H2×D2
则输出矩阵的大小计算公式为：
W 2 = ( W 1 − F ) / S + 1 W_2=(W_1 - F)/S + 1 W2=(W1−F)/S+1
H 2 = ( W 1 − F ) / S + 1 H_2=(W_1- F)/S + 1 H2=(W1−F)/S+1
D 2 = D 1 D_2=D_1 D2=D1
池化层对输入体的每个深度切片独立地进行降采样。
- 左：在此示例中，尺寸为[224x224x64]的输入体与过滤器进行池化，步幅为2，变为尺寸为[112x112x64]的输出体；保留深度。
- 右：最常见的降采样操作是max，即最大池化。此处显示的步幅为2，即，取4个数（不同颜色2x2方阵）中的max。
在实践中，最大池化层只有两种常见变化：
- F = 3 ，S = 2（也称为重叠池）
- F = 2 ，S = 2（更常见）-—— 感受野尺寸过大是不好的。
全连接层（FC）
全连接层在卷积神经网络尾部，两层之间所有神经元都有权重连接（连接所有的特征），将输出值送给分类器（如softmax分类器）得到最终的输出。
reference
[1]深入学习卷积神经网络中卷积层和池化层的意义
[2]为什么要用卷积神经网络？