目标检测算法复习：SPP-Net算法

一、前言

上次看完R-CNN算法，就觉得其非常原始，光是一张图就要做2000次卷积操作（加黑是因为 R-CNN 与 SPP-Net 之间最大区别就是这点）。想一想就觉得它会有很多的改进空间。继续目标检测算法的学习时，发现 R-CNN 和 Fast-RCNN之间还有个 SPP-Net ，学习当中发现一些博客写的很好，拿出来分享，自己再做些补充：
https://blog.csdn.net/forever__1234/article/details/79910175 （这篇首选）；
https://blog.csdn.net/xjz18298268521/article/details/52681966 （这篇补充）；

二、SPP-Net算法出现的原因

SPP-Net算法的前面一个算法 R-CNN算法，它虽然是个开创性的目标检测算法。但是它的缺点十分明显：
① CNN网络后面接的FC层需要固定的输入大小，限制网络的输入大小 。每一个候选区域要被处理成 227x227大小的图，拉伸过程中导致图片失真，对模型性能不利；
② 候选区域会塞给CNN网络用于提取特征向量的，这会有大量的重复计算，造成的计算冗余。一张图要卷积2000次，而且分类器、回归器都是分散、笨重的。导致人们记住的只有它的缺点。

先上图吧，模型基本没变什么，包括分类器、回归器也是沿用了R-CNN的设计（这个我在论文里没看到，可能没细看，看别人讲的），SPP-Net欲解决的问题主要是上面两点，对于其他的倒没改进什么。 layer8 处在R-CNN里是个最大池化，在SPP-Net里换成了空间金字塔池化（Spatial Pyramid Pooling），而且有三种尺寸的池化核，这个在下面细说。

1.测试过程

还是先说测试，再说训练，促进理解。
① 首先通过选择性搜索，对待检测的图片进行搜索出2000个候选窗口，这一步和 R-CNN 相似。不过不同的是，我们只是获得2000个 region 的位置信息就好了，下面的操作与这些 region 没什么关系了；

② 特征提取阶段，这一步就是和 R-CNN 最大的区别了。把①中的待检测的图片，输入CNN中，进行一次性特征提取，得到feature maps，然后在feature maps中找到各个候选框的区域，再对各个候选框采用金字塔空间池化，提取出固定长度的特征向量；
注：由这可看出，SPP-Net里一次前向传播可以处理所有的候选区域，而 R-CNN 一次只能处理一个候选区域。同样一张图片，SPP-Net 只需一次提取特征操作，而 R-CNN 需要2000次。正是因为如此，SPP-Net检测速度是大大加快，论文里说比 R-CNN 快24-102倍。

③ 最后一步也是和R-CNN一样，采用SVM算法进行特征向量分类识别，线性回归器进行位置回归。
思考：怎么在 feature map 找到对应的候选区域？这个我们下面说。

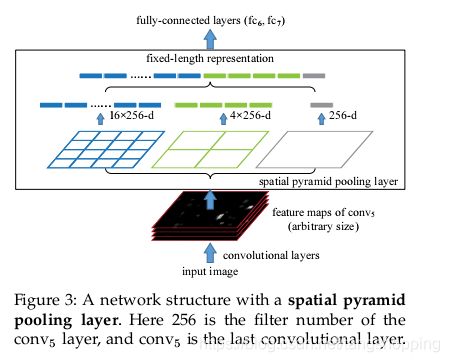
如上图，三种尺寸的池化核，每张 feature map 上、每个候选区域 输出三种结果的feature map ----4x4 , 2x2 , 1x1 ，将结果 reshape 后再拼接，则每个候选区域在256张 feature map 上的结果输出为 （16+4+1）*256 =5376，一张图上 2000个候选区域则有 （2000,5376）的特征 。
关于空间金字塔池化的相关参数，这里稍微说下。如果输入的 feature map 尺寸是 a,则空间金字塔的池化核大小为 a/n (向上取整)，步长为 a/n (向下取整)，n 取值为 1、2、4 。
注：测试图片大小虽说是任意尺寸，不过作者还是建议要大于180，因为224的输入，其 feature map大小为 13x13，输入为180时，肯定更小了，如果再小，可能每个候选框所能提取的特征不多，甚至一些小的候选框会没法在 feature map 上定位。

2.训练过程

训练分为两种，单尺度训练 与 多尺度训练。

（1）单尺度训练

直接从原图中截取 224x224 大小的图片输入模型，而不是输入候选框。输入后先做卷积、spp之类操作提取特征，之后的训练流程与R-CNN一样。
单尺度训练的目的是为了验证SPP池化的效果，结果表明该算法是有作用的，模型精度提升了。

（2）多尺度训练

多尺度训练意思为输入图片的尺寸不止 224x224 这一种，此外还有 180x180、S x S（S 代表输入图片的尺寸）。
Ⅰ 输入为 224x224 ，224x224的输入图片也是直接从图片中截取；
Ⅱ 输入为 180x180 ，不同的是，它不是直接从图中截取。而是由 224x224 的图片 resize 而来。所以，两者的差异就是分辨率不一样，其余都一样；
Ⅲ 输入为 SxS ，S的取值范围是180-224，每次随机均匀的挑选一个尺寸训练一个 epoch。
Ⅳ 其他训练流程与R-CNN类似，SPP-Net在这方面并没有作改进。

此外，为了减少训练时的运算开销与训练时间，每种尺寸会完整的训练一个 epoch，再切换成其他尺寸的图片。在训练中作者发现，不同尺寸下的收敛速度是差不多的。要注意的是，不同尺寸下的模型，其算法结构是不变的，这意味着其参数是共享的，这是SPP-Net的核心思想。多尺度的训练也是为了模拟测试时的任意尺寸的图片输入，同时可利用现有的、优化好的、固定的模型继续训练。
关于图片的预处理，论文中介绍了两种。不过疑惑的是，这两种预处理方法全是训练时用的，测试的预处理我没有看到（我并没有好好看一遍论文，只是大致看了下想看的，如果有发现，请提醒我，谢谢。）。
① 在 ImageNet 数据集中，作者是先算出 224x224 图片的均值，然后以该均值为图片像素，就获得了一张224x224的均值图片，当尺寸不是224时，只需将其 resize 至想要尺寸即可（此处我一直没看明白，如有大神，麻烦指点一下迷津）；
② 在Pascal VOC2007 和 Caltech101 数据集中，每个像素每个通道减去一个确定的数----128即可。

三、基于感受野的特征坐标映射

下面来说说位置映射问题，具体看我给出的链接，他们讲的太详细了，我作补充就好。只不过在下面写了我看映射公式的疑惑之处，免得你们烦恼。我相信我这下面看懂以后，整个映射公式的推导已经明白了。
1.看其他人博客的时候，他们只是给出下面公式，而公式怎么来的，他们也不清楚，让我很无语。先贴出公式：

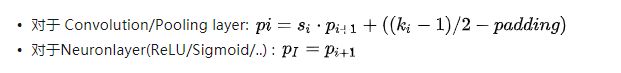
如上图：
p_i , p_i+1 是 feature map 上的坐标，一般是 feature map 中心点坐标；
k_i 是卷积核尺寸；
s_i 是步长；
padding 是一边填充的像素数目，两个方向上的填充总数就是 (2 X p)。
初见这个公式，一脸懵逼，本来想看看前辈的经验，结果发现前辈们只是把公式摆出来。好吧，也许是在锻炼我这只菜逼，在看了半天之后（智商不够，时间来补了），终于有所心得，摆出来和大家分享一下，抛砖引玉。有图能容易理解，如下

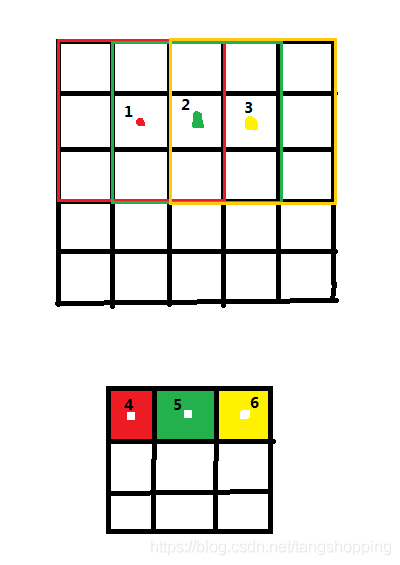
假设 s = 1, k = 3, padding = 0, p_i = p1 = 2.5 ，2.5就是上面 5 x 5 map的中心点的x坐标，同样可以得出下面3 x 3 map的坐标 p_i+1 = p2 = 1.5 。由公式得：
p1 = s x p2 + (k - 1)/2 - padding

2.先说说 s x p2 是什么意思，由图可知 3 x 3 map 里每一个 cell 都是由上面 5 x 5 map 中9个cell卷积而来（特意颜色给你们搞成对应的了）。对于 5 x 5 map来说，它的中心点是从1点开始往右平移的（在这只考虑横坐标方向，减少工作量），它中心点平移几次是看下方 3 x 3 map 的中心点x坐标大小的。
① 如果 p2 = 0.5 (4号点) ,那说明 5 x 5 map的中心点没有往右平移；
② 如果p2 = 1.5 (5号点)，则说明 5 x 5 map的中心点往右平移了一次，平移多远呢，平移了 1 x s 的距离，就是说 从1号点到2号点了；
③ 如果 p2 =2.5 (6号点) ,则说明5 x 5 map的中心点往右平移了两次，平移了 2 x s 的距离，就是说从1号点到3号点了。
注：我p2都是向下取整的，因为平移次数肯定是个整数。实际中p2本来就是个整数。

3.再说说 (k - 1)/2，我们上面算平移距离是从1号点开始算的，1号点并不是0点，它的横坐标是1.5，因为我们少算了这1.5，所以要加上它，它其实就是卷积核尺寸的一半，即 k/2，看到这你们会问公式里是 (k - 1)/2，到我这怎么变成 k/2 了，这个下面再说。
现在我们把p1算出来 ：
p1 = s x p2 + k /2 - padding = 1x1 + 3/2 - 0 = 2.5

抛开 s x p2 的实际意义不看,用上面公式求得 p1 有（其实这也是种理解方式）：
p1 = s x p2 + ( k-1) /2 - padding = 1x1.5 + (3-1)/2 - 0 = 2.5
其实也可以证明出来。

4.pandding 的话，已经没什么悬念了，你们自己推演一下。主要是上面两个公式有点绕。

5.现在来说说为什么 (k - 1)/2 变成了 k /2 ，因为算法中的中心点坐标是没有小数的，所以 我们需要把一号点往左平移0.5，用公式表示出来就是 (k/2) - (1/2) = (k - 1)/2,所以 p1 ,p2的实际坐标是 p1 = 1,p2 = 2。
看到这，可能你们会好奇，这样粗暴地处理数据不会对下面结果影响很大吗？我会告诉你没关系，如果你往下看，你会发现接下来运算有很多粗暴地化简，恐怕对数据的影响更大，最后的映射公式都只是想尽量靠近理论中心点，而且这个误差对于整张图来说算不了什么，所以各位心安。