图像处理Task01图像插值算法
基于图像缩放的插值算法
在图像处理中，插值算法应用广泛，但本渣能力有限，只能阐述基于图像缩放的简单插值算法
1.最近邻插值算法原理
首先定义一个3*3的256级灰度图像（三通道的彩色图像与之类似，只不过要在每个通道都计算一次）
原图像的像素矩阵为：
[ 234 38 22 67 44 12 89 65 63 ] (1) \left[ \begin{matrix} 234 & 38 & 22 \\ 67 & 44 & 12 \\ 89& 65 & 63 \end{matrix}\right] \tag{1} ⎣⎡2346789384465221263⎦⎤(1)
在图像处理中常用的坐标系定义方式为：
x从左到右，从0开始；y从上到下，从0开始
如果把原图像放大为4*4大小的目标图像，则初始矩阵为：
[ x x x x x x x x x x x x x x x x ] (2) \left[ \begin{matrix} x & x & x&x \\ x & x & x&x \\ x& x& x&x\\ x&x&x&x \end{matrix}\right] \tag{2} ⎣⎢⎢⎡xxxxxxxxxxxxxxxx⎦⎥⎥⎤(2)
首先确定目标图像最上角的像素值，是通过四舍五入的方法求取目标图像的坐标对应的原图像的坐标，然后原图像在该点的像素值直接作为目标图像在该点的像素值，进而把该矩阵中的每一个元素求解出来。具体四舍五入的方法以及像素求取公式如下：
f ( d s t X , d s t Y ) = h ( d s t X s r c W i d t h d s t W i d t h , d s t Y s r c H e i g h t d s t H e i g h t ) \begin{array}{c} f(dst_{X}, dst_{Y}) = h(\frac{dst_{X}src_{Width}} {dst_{Width}}, \frac{dst_{Y}src_{Height}} {dst_{Height}}) \end{array} f(dstX,dstY)=h(dstWidthdstXsrcWidth,dstHeightdstYsrcHeight)
f ( 0 , 0 ) = h ( 0 , 0 ) f ( 0 , 1 ) = h ( 0 , 0.75 ) = h ( 0 , 1 ) f ( 0 , 2 ) = h ( 0 , 1.50 ) = h ( 0 , 2 ) f ( 0 , 3 ) = h ( 0 , 2.25 ) = h ( 0 , 2 ) . . . \begin{array}{c} f(0,0)=h(0,0) \ f(0,1)=h(0,0.75)=h(0,1) \ f(0,2)=h(0,1.50)=h(0,2) \ f(0,3)=h(0,2.25)=h(0,2) \ ...\ \end{array} f(0,0)=h(0,0) f(0,1)=h(0,0.75)=h(0,1) f(0,2)=h(0,1.50)=h(0,2) f(0,3)=h(0,2.25)=h(0,2) ...
最终结果为：
[ 234 38 22 22 67 44 12 12 89 65 63 63 89 65 63 63 ] (3) \left[ \begin{matrix} 234 & 38 & 22&22\\ 67& 44 & 12&12 \\ 89& 65& 63&63\\ 89&65&63&63 \end{matrix}\right] \tag{3} ⎣⎢⎢⎡234678989384465652212636322126363⎦⎥⎥⎤(3)
注：计算机里的图像是数字图像，像素是其最小单位，不会出现小数，所以必须将小数变成整数，这里采用四舍五入的整数近似。
总结：这是一种最基本的插值方法，效果不是最好的，对于放大的图像有很严重的失真，其根本原因就是直接采取四舍五入的方法得到目标图像的坐标。
2.双线性内插值算法原理
**前言：**相对于最近邻插值算法，它充分利用了原图像中虚拟点（即通过目标图像直接求出来的原图像的坐标），四周的四个真实存在的像素值来共同决定目标图中的一个像素值，因此缩放效果比简单的最近邻插值要好很多。
算法：
对于一个目标像素，设置坐标通过反向变换得到的浮点坐标 ( i + u , j + v ) \begin{array}{l}(i+u,j+v)\end{array} (i+u,j+v),其中（i，j）为浮点坐标的整数部分，u，v为浮点坐标的小数部分，则这个像素值由原图像中坐标为（i，j), (i+1,j), (i,j+1), (i+1,j+1)所对应的周围四个像素点的值决定，具体计算公式为：
f ( i + u , j + v ) = ( 1 − u ) ( 1 − v ) f ( i , j ) + ( 1 − u ) v f ( i , j + 1 ) + u ( 1 − v ) f ( i = 1 , j ) + u v f ( i + 1 , j + 1 ) \begin{array}{l} f(i+u, j+v)=(1-u)(1-v)f(i,j)+(1-u)vf(i,j+1)+u(1-v)f(i=1,j)+uvf(i+1,j+1) \end{array} f(i+u,j+v)=(1−u)(1−v)f(i,j)+(1−u)vf(i,j+1)+u(1−v)f(i=1,j)+uvf(i+1,j+1)
从上面的表达式很容易发现，如果有一个虚拟点为（0.75，0.75），它离（1，1）更近，那么（1，1）点对应的像素值所起的决定性作用更大一些，uv=0.750.75,权重更大，而（0，0）离（0.75，0.75）远，故（1-u）（1-v）=0.250.25，权值较小。
虚拟点的计算公式为：
( d s t X , d s t Y ) = ( d s t X s r c W i d t h d s t W i d t h , d s t Y s r c H e i g h t d s t H e i g h t ) \begin{array}{c} (dst_{X}, dst_{Y}) = (\frac{dst_{X}src_{Width}} {dst_{Width}}, \frac{dst_{Y}src_{Height}} {dst_{Height}}) \end{array} (dstX,dstY)=(dstWidthdstXsrcWidth,dstHeightdstYsrcHeight)
而对于双线性插值公式的作用与上面直接求解的方法殊途同归，是连续公式的离散化应用，具体的原理可参考这里
至此，双线性插值法的核心介绍完毕，但是单纯按照上文实现的插值算法只能勉强完成插值的功能，速度和效果都不会理想，在具体代码实现的时候有些小技巧。参考OpenCV源码以及网上博客整理如下两点：
源图像和目标图像几何中心的对齐。
将浮点运算转换成整数运算
由于笔者水平有限，该部分内容尚未完全理解，故给出参考博客
3.Python-opencv 实现
分别将原图像的宽高变为原来的0.5倍和1.5倍，观察输出结果
import cv2
img = cv2.imread('D:/Mechine_learning_data/lena512.bmp',cv2.IMREAD_GRAYSCALE)
img1 = cv2.resize(img,dsize=None,fx=0.5,fy=0.5,interpolation = cv2.INTER_NEAREST)
img2 = cv2.resize(img,dsize=None,fx=0.5,fy=0.5,interpolation = cv2.INTER_LINEAR)
img3 = cv2.resize(img,dsize=None,fx=1.5,fy=1.5,interpolation = cv2.INTER_NEAREST)
img4 = cv2.resize(img,dsize=None,fx=1.5,fy=1.5,interpolation = cv2.INTER_LINEAR)
img5 = cv2.resize(img,dsize=None,fx=1.5,fy=1.5,interpolation = cv2.INTER_CUBIC)
print('Smaller_image_nearest:',img1.shape)
print('Smaller_image_linear:',img2.shape)
print('Bigger_image_neraest:',img3.shape)
print('Bigger_image_linear:',img4.shape)
print('Bigger_image_CUBIC:',img5.shape)
print('Original Dimensions:',img.shape)
输出结果为：
Original Dimensions: (512, 512)
Smaller_image_nearest: (256, 256)
Smaller_image_linear: (256, 256)
Bigger_image_neraest: (768, 768)
Bigger_image_linear: (768, 768)
Bigger_image_CUBIC: (768, 768)
进一步显示图像信息，由于我们对比这几种方法的效果只是在图像放大的时候更明显，因为放大图像才需要插入新值，所以只对比放大图像的信息：
cv2.imshow("Bigger_neraest",img3)
cv2.imshow("Bigger_linear",img4)
cv2.imshow("Bigger_CUBIC",img5)
cv2.waitKey(0)
cv2.destroyAllWindows()
输出结果分别为：
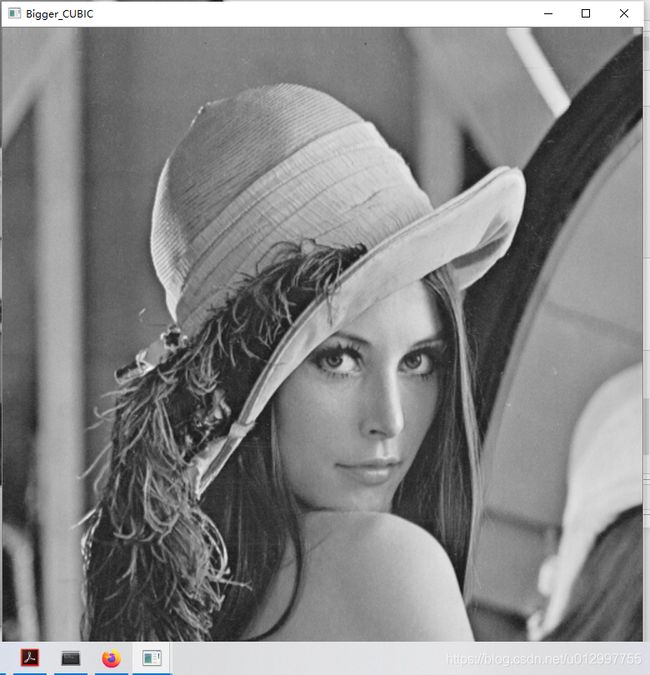注：最后一种方法是基于4x4像素邻域的3次插值法，它的原理与双线性内插值算法相似。但是效果会更好一些，所以拿来做个比较。
通过观察可以发现，最近邻插值的放大图像，它的边缘特征以及很明显的出现了失真现象，即帽子的边沿出现像素块，效果是最差的，而4*4像素邻域的3次插值法效果更好一些，但是算法也相对更复杂，所以经常用到的便是双线性内插值算法
The End，Opencv的插值算法还有很多，读者可以自行阅读这篇博客