策略梯度与A2C算法

从Q learning到策略梯度

在解决MDP问题的算法中，Value Base类算法的思路将关注点放在价值函数上，传统的Q Learning等算法是一个很好的例子。Q Learning通过与环境的交互，不断学习逼近(状态, 行为)价值函数$Q(s_t,a_t)$，而策略本身即选取使得在特定状态下价值函数最大的动作，即$a_t={\mathrm{argmin}}_{a}Q(s_t,a)$ ， 具体算法如图1所示。

其中$Q(S,A)\leftarrow Q(S,A)+\alpha \left[R+\gamma {\max }_{a}Q\left(S^{\prime },a\right)-Q(S,A)\right]$一步即时序差分法的价值函数逼近过程，具体原理详见。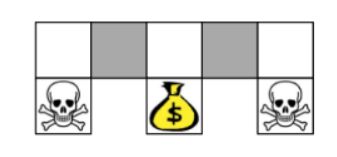

Q learning算法已经能解决许多问题，但最致命的一点是: 在确定环境$s_t$下，策略选择的行动总是确定的，这对于很多场景来说，并不适用。例如玩剪刀石头布的时候，如果出拳的策略是一定的话，就很容易被对手察觉并击破。同时，Q learning也无法解决状态重名的问题。具体地说，状态重名是指在两个现实中的状态，在建模中表现出来的state是一样的，也就是$s_t$向量的每个维度都相等。如下图中格子世界的例子，如果状态被建模成二维向量，维度分别表示左右是否有墙阻挡，那么图中两个灰色格子的状态向量是一样的，于是他们在Q learning中学习到的策略会选择一样的行动，但矛盾的是: 如果选择向左走，对于第一个格子就是一次失败的决策。如果选择向右走，对于第二个格子来说就是一次失败的决策。特别是如果使用$ϵ-greedy$策略时，很可能在第一个灰格子会不停选择向左的行动，直到一次$ϵ$概率的事件发生时，才有可能选择一次随机行为，从而有机会跳出这个坏处境。这时候还不如直接使用随机策略管用。
针对上述种种缺点，策略梯度法应运而生。
首先，我们需要明确的是，强化学习的最终目的是最大化价值函数。Q learning算法的思路比较绕，Q learning并没有直接去最大化价值函数，而是思考: 在给定状态$s_t$下，做出动作$a_t$会得到什么样的回报？ 得到答案之后，每次都贪婪地选择回报最大的那个动作。 可是为什么我们不直接思考: 在给定状态下，做出什么样的动作，才能让回报最大化？ 策略梯度就是这样一个直接的算法。

具体地说，策略梯度算法将策略建模成为${\pi }_{\theta }(s,a)$，表示在$s$状态下选择$a$动作的概率，其中$\theta$为参数。并且将负回报函数作为损失函数，应用梯度下降法将期望奖励最大化。定义为

$$J(\theta )=\sum _{s}d(s)\sum _a{\pi }_{\theta }(s,a)\mathcal{R}(s,a)\text{\hspace{1em}(1)}$$

这样，(1)式对参数$\theta$求梯度得到

$$\begin{array}{rl}{\nabla }_{\theta }J(\theta )& =\sum _{\mathbf{s}\in S}d(s)\sum _{a\in A}{\pi }_{\theta }(s,a){\nabla }_{\theta }\log {\pi }_{\theta }(s,a){\mathcal{R}}_{s,a}\\ & ={\mathbb{E}}_{{\pi }_{\theta }}\left[{\nabla }_{\theta }\log {\pi }_{\theta }(s,a)\mathcal{R}(s,a)\right]\end{array}\text{\hspace{1em}(2)}$$

式子(2)的期望通过均值代替得到

$${\nabla }_{\theta }J(\theta )=\frac{1}{N}\sum {\nabla }_{\theta }\log {\pi }_{\theta }(s,a)\mathcal{R}(s,a)\text{\hspace{1em}(3)}$$

于是我们得到了蒙特卡洛策略梯度算法

AC算法

从式子(3)来看蒙特卡洛策略梯度算法在策略梯度更新的过程中，考虑的是即时奖励$v_t$，而即时奖励具有较大噪声，为了得到更稳定的表现，可以使用长期回报来替代即时奖励。具体如式(4):

$$\begin{array}{rl}{\nabla }_{\theta }J(\theta )& =\sum _{\mathbf{s}\in S}d(s)\sum _{a\in A}{\pi }_{\theta }(s,a){\nabla }_{\theta }\log {\pi }_{\theta }(s,a)G_{s,a}\end{array}\text{\hspace{1em}(4)}$$

其中$G_{s,a}=\sum {\lambda }^n{\mathcal{R}}_n$定义为(s,a)的长期回报, 根据Q函数的定义$Q(s,a)=\mathbb{E}[G_{s,a}|s,a]$,于是式子(4)使用长期回报期望$Q(s,a)$直接替代长期回报得到式(5)

$${\nabla }_{\theta }J(\theta )={\mathbb{E}}_{{\pi }_{\theta }}\left[{\nabla }_{\theta }\log {\pi }_{\theta }(s,a)Q(s,a)\right]\text{\hspace{1em}(5)}$$

于是根据(5)式我们可以得到$\Delta \theta ={\nabla }_{\theta }\log {\pi }_{\theta }(s,a)Q(s,a)$，用这种方式更新参数的就是Actor-Critic算法，简称AC算法。其中Critic就是$Q(s,a)$，本质上就是梯度权值，也可以说是评价梯度的重要性。假设我们使用的Q函数是一个简单的线性函数$Q_w(s,w)=\varphi (s,a{)}^{T}w$，那么AC算法具体的过程可以给出如下图。

A2C算法

AC算法使用的Q函数是一个随机初始化的函数，需要在交互中学习逼近真正的$\hat{Q}$，这意味着我们在梯度更新中引入了噪声，或者说方差。为了解决这个问题，A2C引入了Baseline的概念。具体地说是通过在(5)式中引入一个Baseline函数$\mathcal{B}$得到(6)式子

$${\nabla }_{\theta }J(\theta )={\mathbb{E}}_{{\pi }_{\theta }}\left\{{\nabla }_{\theta }\log {\pi }_{\theta }(s,a)\left[Q(s,a)-\mathcal{B}\right]\right\}\text{\hspace{1em}(6)}$$

且要求(5)式与(6)相等(期望不变)但方差更低。事实上只要$\mathcal{B}$ 只与s相关而与a无关，即$\mathcal{B}(s)$就可以达到期望不变的目的。简单地将(6)式子展开即可得到这个结论

$$\begin{array}{rl}{\nabla }_{\theta }J(\theta )& ={\mathbb{E}}_{\theta }\left[{\nabla }_{\theta }\log {\pi }_{\theta }Q(s,a)\right]-\mathbb{E}\left[{\nabla }_{\theta }\log {\pi }_{\theta }(s,a)\mathcal{B}(s)\right]\\ & ={\mathbb{E}}_{\theta }\left[{\nabla }_{\theta }\log {\pi }_{\theta }Q(s,a)\right]-\sum _{s\in S}{d}^{{\pi }_{\theta }(s)}\mathcal{B}(s){\nabla }_{\theta }\sum _{a\in A}\log {\pi }_{\theta }(s,a)\\ & ={\mathbb{E}}_{\theta }\left[{\nabla }_{\theta }\log {\pi }_{\theta }Q(s,a)\right]\end{array}$$

第二个等号交换了求导与求和的顺序，并且将与a无关的$\mathcal{B}(s)$提到求和符号外，于是根据定义${\sum }_{a\in A}{\pi }_{\theta }(s,a)=1$，而常数的梯度等于0。于是现在对于函数$\mathcal{B}(s)$只剩下让方差更低这一约束了。首先来看方差

$$\begin{array}{r}Var(X)=\mathbb{E}\left[(X-\overline{X}{)}^2\right]=\mathbb{E}(X^2)-[E(\overline{X}){]}^2\end{array}$$

接下来我们让方差对函数$\mathcal{B}(s)$的导数为0

$$\begin{array}{rl}\frac{\partial Var(X)}{\partial \mathcal{B}(s)}& =\frac{\partial Var(X)}{\partial X}\cdot \frac{\partial X}{\mathcal{B}(s)}\\ & =2E[X\cdot \frac{\partial X}{\partial \mathcal{B}(s)}]\\ & =0\end{array}$$

然后带入$X={\nabla }_{\theta }\log {\pi }_{\theta }(s,a)\left[Q(s,a)-\mathcal{B}(s)\right]$得到

$$\begin{array}{rl}& \sum _{s\in S}{d}^{{\pi }_{\theta }}(s)\sum _{a\in A}[{\nabla }_{\theta }\log {\pi }_{\theta }(s,a){]}^2[Q(s,a)-\mathcal{B}(s)]\\ & =\sum _{s\in S}{d}^{{\pi }_{\theta }}(s)\sum _{a\in A}[{\nabla }_{\theta }\log {\pi }_{\theta }(s,a){]}^{2}Q(s,a)-\sum _{s\in S}{d}^{{\pi }_{\theta }}(s)\mathcal{B}(s)\sum _{a\in A}[{\nabla }_{\theta }\log {\pi }_{\theta }(s,a){]}^2\\ & =0\end{array}\text{\hspace{1em}(7)}$$

解得

$$\mathcal{B}(s)=\frac{{\sum }_{a\in A}[{\nabla }_{\theta }\log {\pi }_{\theta }(s,a){]}^{2}Q(s,a)}{{\sum }_{a\in A}[{\nabla }_{\theta }\log {\pi }_{\theta }(s,a){]}^2}\text{\hspace{1em}(8)}$$

式(7)给出了使得方差最小时得$\mathcal{B}(s)$，但也可以看到其计算复杂度十分高。事实上我们可以在计算复杂度和噪声指标上做权衡。从式子(7)中其实我们可以看到只要$\mathcal{B}(s)$逼近$Q(s,a)$且与a无关，即可得到一个接近最优解得方案。可以非常直觉地想到取状态价值函数$V(s)=\mathbb{E}[G_{s,a}|s]$作为$\mathcal{B}(s)$，即

$$\mathcal{B}(s)=V(s)\text{\hspace{1em}(9)}$$

最后，令$A(s,a)=Q(s,a)-V(s)$为优势函数(动作a相对平均表现的优势)，可以得到A2C算法的梯度公式

$${\nabla }_{\theta }J(\theta )={\mathbb{E}}_{{\pi }_{\theta }}\left[{\nabla }_{\theta }\log {\pi }_{\theta }(s,a)A(s,a)\right]\text{\hspace{1em}(10)}$$

在工程实现上，我们并不需要维持两套参数去分别交互逼近$Q(s,a)$和V(s)。具体地说，我们可以使用${\delta }^A=r+\lambda V(s^{\prime })-V(s)$来替代$\delta =r+\lambda Q(s^{\prime },a^{\prime })-Q(s,a)$，因为根据定义$\mathbb{E}(\delta )={\delta }^A$。并且恰好${\delta }^A$就是$A(s,a)$的无偏估计，这是因为根据Q函数的定义有$ \mathbb E[r+\lambda V(s’)|s,a] = Q(s,a)$。所以实际上实现A2C算法的时候，只需要维持一套参数用于估计$V(s)$，并且做梯度下降更新参数的时候可以使用

$$\Delta \theta =\alpha {\nabla }_{\theta }\log {\pi }_{\theta }(s,a)(r+\lambda V(s^{\prime })-V(s))\text{\hspace{1em}(11)}$$