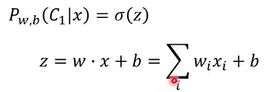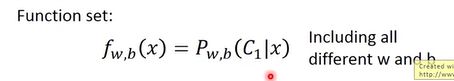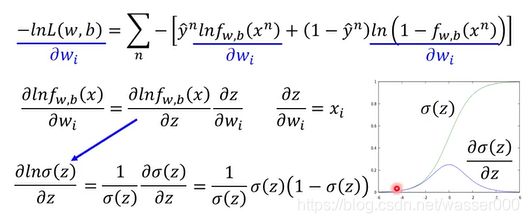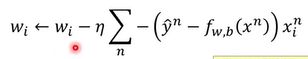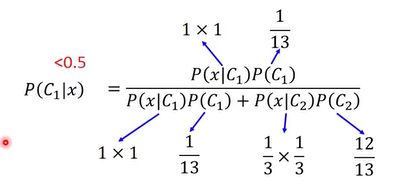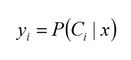李宏毅机器学习笔记（6）：logistic Regression

       这一部分是接着上一部分进行描述的，上一部分，我们把使用贝叶斯公式得到的结果推导，发现结果是一个线性的函数，我们针对这个函数，试试可不可以把这个函数求解出来。

很容易发现，这是一个回归问题，我们就把他称作是逻辑回归，做这个回归问题一步一步来吧：

1 模型选择 function set

       首先我们还是需要选择合适的模型，确立我们的目标。

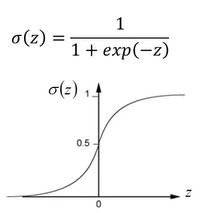
       上一节了解了我们的目标确定相关的P(C1|x)，使用它进行一个判决，高于阈值便确定x从属于c1类。

       同样，我们还知道P(C1|x)的函数应该是一个σz函数，而z的函数模型就是一个线性函数。我们的目的就是，通过拟合出z的函数模型，就能更好地求解出σz函数，之后进一步求解PC1x。

我们的函数集就是：

       这样就可以把问题大大简化了。

 

1. 在这里对比一下逻辑回归和线性回归在第1步的区别

逻辑回归和线性回归都是在寻找线性模型的偏差与斜率，但是两者差距很大，逻辑回归的目的是为了更好的进行分类问题，而线性回归目的是在进行回归问题。

       在第一步中，两者最明显的区别是输出的不同，逻辑回归由于经过了sigmoid函数的处理，他的输出结果只能在0到1之间，而线性回归则没有这个约束。

2 模型优势 goodness of function

第二步，我们要分析一下我们的模型，确定一下这个模型的好坏。这个问题的目的还是在进行一个分类的问题。我们把训练集的数据取出来，之后用模型学习得到分类结果，这个结果可以进行判定这个模型的好坏。

       这个模型中，求解函数在于求解w和b，而求解w和b，我们之前提到过，可以使用最大似然估计进行求解。如图2-1.

图2-1 第二步目的

       之后就可以对训练集使用最大似然了，如图2-2，对似然函数进行处理，取负对数，这样需要让似然函数最大就变成了，需要让变形后的似然函数最小。在这里可以告诉大家了，这里我们得到了的差不多就是损失函数了，之后需要进行一些变形。

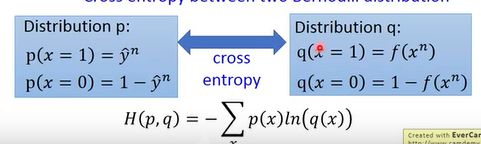
       对变形后的似然函数就可以进行处理了，ln函数相乘可以变化成相加运算，得到图2-2最下面的式子，每一项都变成了下式：

       这个式子学过信息论的肯定会非常熟悉了也非常好理解了，这就是交叉信息熵（0-1分布的）。这个y代表了每个样本的所属类，如图2-2上部分，如果样本为x1，那么所属于C1类，他的y就是1，如果所属C2类，他的y就是0。这样我们可以约掉其中的一些项。

图2-2 最大似然估计的变形

交叉熵这个概念学过信息论会非常容易理解，这里额外提一下，交叉熵是由信息熵所推到来的。交叉熵可以衡量两个概率的相似性（差异性），如果这两个分布完全一样，那么他们的交叉熵就是0。

       机器学习中，交叉熵损失函数算是一个非常重要的点了，如果说学习得到的模型，分类之后样本的分布，和实际样本的分布求交叉熵，我们一定希望这两个分布越一致越好，那么让交叉熵越小越好就可以了，这就是交叉熵损失函数。

同时，使用sigmoid函数在梯度下降时能避免均方误差损失函数导致的学习速率降低的问题，因为学习速率可以被输出的误差所控制。

 

1. 在这里对比一下逻辑回归和线性回归在第2步的区别

可以看图2-3，第二步中，两者的区别是在于损失函数逻辑回归中损失函数是交叉熵损失函数，而在线性回归中，损失函数就是我们之前提到的均方误差。

图2-3 第二步区别

3  find the best function 求解最好的模型

之后需要求出损失函数最小时的w和b，此时就可以使用梯度下降了。但是进行梯度下降之前我们先进行一系列的化简。

对损失函数进行简单的求偏导（求梯度），由级数的知识可以知道，可以对内部分别求偏导，前一部分就成了先f对z，后z对w求偏导。计算如图3-1，后一部分同理。

图3-1 第三步求偏导

化简之后得到的式子如下图3-2，我们已看出最后的化简结果不是很难。

图3-2 第三步求偏导后的化简结果

就可以构造出梯度下降的式子了：

这里来分析一下上式以便我们更好地去理解它。可以看出，梯度下降的一次迭代步长取决于三部分，一部分是学习率η，一部分是x也就是我们的样本数据，另一部分就是y-fw,bxn。前两部分其实都很好理解，最后一部分刻画的是y和fw,bxn之间的差距，也就是说刻画的是样本理想的分类目标y和现在当前的模型预测值fw,bxn之间的差距。如果这个差距越大，我们的步长就会更大，如果离目标越远吗，那么我们的步长就会更大。

1. 逻辑回归和线性回归在第3步的区别

对于第三步（梯度下降），如下图3-3。我们发现了有趣的现象，在逻辑回归和线性回归问题中，确实他们的梯度下降的式子是完全相同的。

但是要注意的是，由于之前的不同，这里逻辑回归的fw,bxn是只能取0到1之间的，而线性回归没有这个限制。

并且，逻辑回归中的y也是只能取值0或1。

图3-3 第三步区别

4 逻辑回归中的损失函数

       知道了逻辑回归的一些基本，那么接下来就分析一些细节的问题。

       我们知道，逻辑回归的损失函数是交叉熵损失函数，而线性回归的损失函数是均方误差损失函数，那么如果我们对分类问题的逻辑回归中使用均方误差损失函数，会造成什么结果呢？

图4-1 逻辑回归和均方误差步骤

 

       上图4-1就是我们使用逻辑回归与均方误差损失函数结合的一个步骤分析，我们可以看到对均方误差损失函数求偏导的结果。

       对这个结果分析，如果实际目标y是1的话，如果f判定为1，此时带入上式发现，损失函数的偏导为0，由于我们的预测与理想结果都为1，所以符合实际情况。

如果此时f判定是0的话，理想目标为1，理想目标与预测目标差距很远，但损失函数的偏导为0，这确实算是一个问题。（f判定为1时类似）

图4-2逻辑回归和均方误差组合结果分析

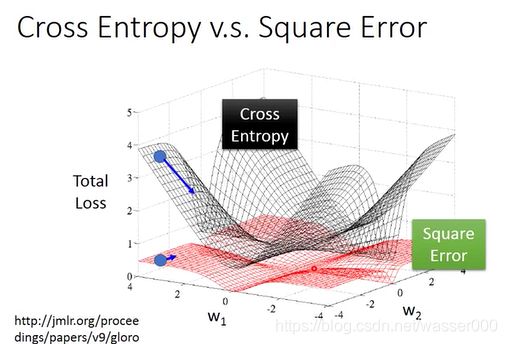
       接着看下图4-3，这是交叉熵损失函数与均方误差损失函数针对这个问题的图象分析。黑色为交叉熵损失函数，红色为均方误差损失函数，坐标轴代表了不同的参数。当离目标原点（中心点）越远时，随着参数的变化，交叉熵损失函数有较大的起伏，较好的体现出了实际的情况，也有利于进一步的梯度下降。

而均方误差损失函数并没有这个效果，同时在距离中心很远的地方，均方误差函数非常平坦，参数更新速度将会很慢。

图4-3交叉熵和均方误差损失函数对比

5 生成模型Generative与判别模型Discriminative

       本文提到的逻辑回归的方法一般称之为Discriminative的方法，而上一次提到的使用高斯分布与贝叶斯公式的方法我们称之为Generative的方法。

       判别模型中，我们直接使用了逻辑回归去找到了w和b，而生成模型中，我们通过使用寻找高斯分布间接获取了w和b。即使使用相同的数据集，这两组w和b也是不一样的，这个差异可能来源于对分布的假设，也可能是来源于其他地方。

图5-1生成模型Generative与判别模型Discriminative

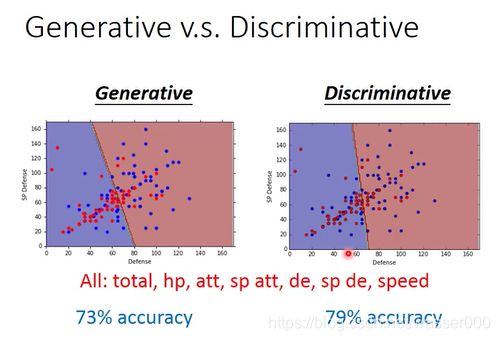
       对于这两个不同的结果，大多文献中，常常听到的结果是判别模型的结果往往是优于生成模型的。在宝可梦属性分类问题上，可以看两者不同的结果，图5-2。

图5-1生成模型Generative与判别模型Discriminative的结果

       对于这个解释我们需要用一个例子去解释：

       可以看图5-2，训练集有13个样本，1个class1，剩下都是class2的，每个样本有两个特征，每个特征可以为0或者1，从图中可以看出这些样本的不同。那么当测试集出现两个特征都是1的情况，会发现什么结果呢？

       如果是我们人类去做的话，直观的看会发现这个样本应该是属于class1。那么如果我们使用朴素贝叶斯（naïve bayes）去做呢？

       朴素贝叶斯属于比较早期的算法了，他认为所有特征的分布都是独立的，那么就有图5-2中右下角的式子了。

图5-2 解释例子

       使用朴素贝叶斯进行计算，我们发现，将这个样本判定为类1的概率竟然小于50%。

图5-3 结果

       在这个例子中，问题就出在了朴素贝叶斯的前提假设，由于朴素贝叶斯认为每一个特征的概率分布都是独立的，所以在这种样本量不是这么大的情况下，出现了这种问题。

       回到生成模型Generative与判别模型Discriminative的问题上，我们在使用生成模型时，往往会进行一系列的假设，假设数据的分布处于一个高斯分布或者什么分布，但是真正的分布是什么我们不知道。

       这是我们在寻找模型之前人为的猜想，这种猜想有时候会使结果并没有那么好，但是有时候会出现较好的效果：

1. 较少的样本时，拥有假设可能效果会好。
2. 样本的噪声较大，假设会帮我们确定较好的方向。
3. 可以从不同来源估算先验概率和与类相关的概率。（比如语言识别中，先验概率是计算好的）

一些情况下其实会将两者结合来处理问题。

6 多分类问题

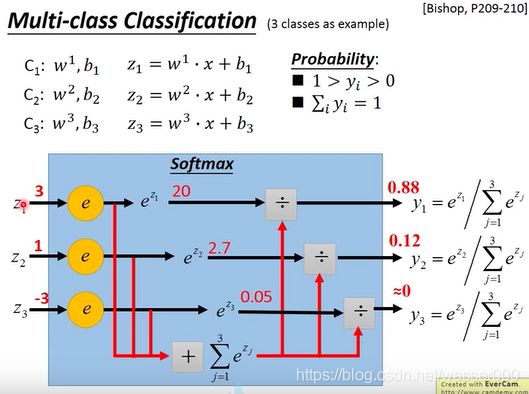
       之后我们将学习多分类问题了，把类的数目增加到3个。这部分只讲过程，不再讲原理了，如图6-1。

图6-1 多分类问题

       在多分类问题中（如图有三类），不同的类（c1，c2，c3）有着不同的w和b，我们使用它得到不同的z值（z1，z2，z3）。使用这些z值一起放入一个softmax函数中，这个函数很好理解，就是先取指数后归一化。得到的结果即为不同的y（y1，y2，y3），y的值在0到1之间，且y之和为1。

       这个y就可以作为概率使用了，这里是可以进行解释的（从概率的角度或者最大熵的角度都可以），这里不多赘述了。

       softmax函数也可以作为深度学习中的激活函数，以后再说。

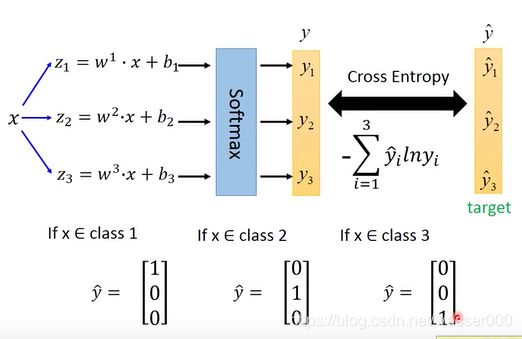
       回顾整个过程，如下图6-2。经过softmax得到的概率就可以和我们训练集中的样本的真实分布求交叉熵。每一个y此时可以用矩阵来表示了，如图很明白。

图6-2 三分类问题过程

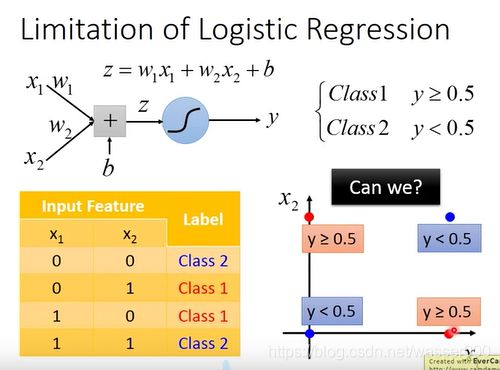
7 逻辑回归的限制

       其实逻辑回归算法是有很强的限制的，此时我们就引入一个机器学习中很有趣的一个问题——异或问题。如图7-1中的表格，如果类1的两个特征是异或关系，类2是同或关系，这种情况下是不可以使用逻辑回归进行分类的。（异或问题周志华老师的西瓜书曾用神经网络解过，也算是一种方法）

图7-1 异或问题

       如果我们坚持想这样做的话，可以使用特征转化将特征转化到适合进行处理的空间中，如图7-2。把原来的特征转化成新的特征，这个例子中，把原有的x1,x2转化成了x1’,x2’， x1’是原特征到[0，0]距离，x2’是原特征到[1，1]距离，得到下图中的结果。

       但是这并不是一种比较好的方法，因为大多数情况下，特征转化不是一件容易的事，更何况这样做似乎就不算是人工智能了，更像是在依靠人自身的能力去寻找合适的分类特征。

图7-2 特征转化

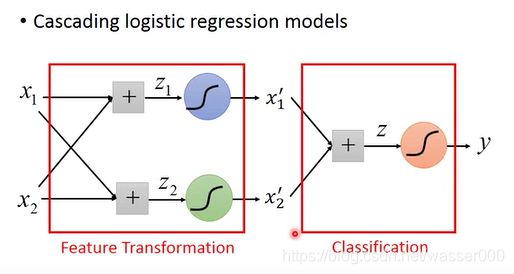
1. 更好的方法

或许我们可以寻找更好的方法，如图7-3，我们可以把多个逻辑回归进行拼接，x1,x2是一组特征输入，之后将下一层的输出作为结果进行下一层的输入。前一层就是在做特征转化，而后一层就是在做分类。

图7-3 逻辑回归的拼接

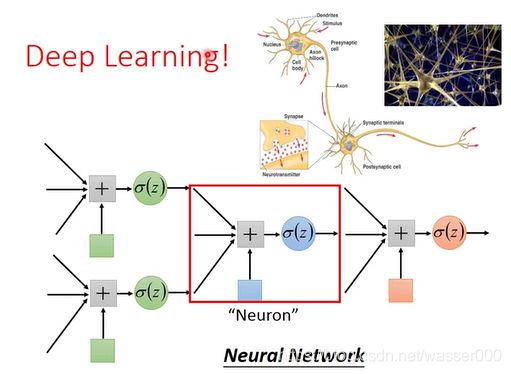
       是不是感觉很有趣！（这段可以看看老师的视频）其实我们这样可以拼起来更多，组成更多层，这些层层叠叠的组成，我们把它称为神经网络，也就是深度学习。

下一章，我们就开始接触深度学习。