from matplotlib.font_manager import FontProperties
import matplotlib.pyplot as plt
import numpy as np
import random
"""
Desc:
梯度上升算法测试函数,求函数f(x) = -x^2+4x的极大值
Parameters:
None
Returns:
None
"""
def Gradient_Ascent_test():
def f_prime(x_old):
return -2 * x_old + 4
x_old = -1
x_new = 0
alpha = 0.01
presision = 0.00000001
while abs(x_new - x_old) > presision:
x_old = x_new
x_new = x_old + alpha * f_prime(x_old)
print(x_new)
"""
Desc:
加载数据
Parameters:
None
Returns:
dataMat - 数据列表
labelMat - 标签列表
"""
def loadDataSet():
dataMat = []
labelMat = []
fr = open('testSet.txt')
for line in fr.readlines():
lineArr = line.strip().split()
dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])])
labelMat.append(int(lineArr[2]))
fr.close()
return dataMat, labelMat
"""
Desc:
绘制数据集
Parameters:
weights - 权重参数数组
Returns:
None
"""
def plotBestFit(weights):
dataMat, labelMat = loadDataSet()
dataArr = np.array(dataMat)
n = np.shape(dataMat)[0]
xcord1 = []
ycord1 = []
xcord2 = []
ycord2 = []
for i in range(n):
if int(labelMat[i]) == 1:
xcord1.append(dataArr[i, 1])
ycord1.append(dataArr[i, 2])
else:
xcord2.append(dataArr[i, 1])
ycord2.append(dataArr[i, 2])
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(xcord1, ycord1, s=20, c='red', marker='s', alpha=.5)
ax.scatter(xcord2, ycord2, s=20, c='green', alpha=.5)
x = np.arange(-3.0, 3.0, 0.1)
y = (-weights[0] - weights[1] * x) / weights[2]
ax.plot(x, y)
plt.title('BestFit')
plt.xlabel('x1')
plt.ylabel('y2')
plt.show()
"""
Desc:
sigmoid函数
Parameters:
inX - 数据
Returns:
sigmoid函数
"""
def sigmoid(inX):
return 1.0 / (1 + np.exp(-inX))
"""
Desc:
梯度上升法
Parameters:
dataMath - 数据集
classLabels - 数据标签
Returns:
weights.getA() - 求得的权重数组(最优参数)
weights_array - 每次更新的回归系数
"""
def gradAscent(dataMath, classLabels):
dataMatrix = np.mat(dataMath)
labelMat = np.mat(classLabels).transpose()
m, n = np.shape(dataMatrix)
alpha = 0.01
maxCycles = 500
weights = np.ones((n, 1))
weights_array = np.array([])
for k in range(maxCycles):
h = sigmoid(dataMatrix * weights)
error = labelMat - h
weights = weights + alpha * dataMatrix.transpose() * error
weights_array = np.append(weights_array, weights)
weights_array = weights_array.reshape(maxCycles, n)
return weights.getA(), weights_array
"""
Desc:
改进的随机梯度上升法
Parameters:
dataMatrix - 数据数组
classLabels - 数据标签
numIter - 迭代次数
Returns:
weights - 求得的回归系数数组(最优参数)
weights_array - 每次更新的回归系数
"""
def stocGradAscent1(dataMatrix, classLabels, numIter=150):
m, n = np.shape(dataMatrix)
weights = np.ones(n)
weights_array = np.array([])
for j in range(numIter):
dataIndex = list(range(m))
for i in range(m):
alpha = 4/(1.0+j+i)+0.01
randIndex = int(random.uniform(0, len(dataIndex)))
h = sigmoid(sum(dataMatrix[randIndex] * weights))
error = classLabels[randIndex] - h
weights = weights + alpha * error * dataMatrix[randIndex]
weights_array = np.append(weights_array, weights, axis=0)
del(dataIndex[randIndex])
weights_array = weights_array.reshape(numIter*m, n)
return weights, weights_array
"""
Desc:
绘制回归系数与迭代次数的关系
Parameters:
weights_array1 - 回归系数数组1
weights_array2 - 回归系数数组2
Returns:
None
"""
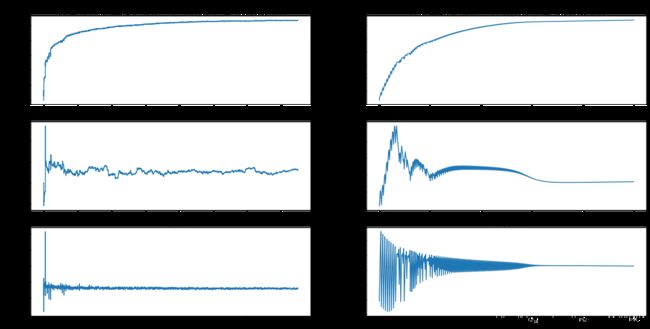
def plotWeights(weights_array1, weights_array2):
font = FontProperties(fname=r"C:\Windows\Fonts\simsun.ttc", size=14)
fig, axs = plt.subplots(nrows=3, ncols=2, sharex=False, sharey=False, figsize=(20, 10))
x1 = np.arange(0, len(weights_array1), 1)
axs[0][0].plot(x1, weights_array1[:, 0])
axs0_title_text = axs[0][0].set_title(u'改进的梯度上升算法,回归系数与迭代次数关系', FontProperties=font)
axs0_ylabel_text = axs[0][0].set_ylabel(u'w0', FontProperties=font)
plt.setp(axs0_title_text, size=20, weight='bold', color='black')
plt.setp(axs0_ylabel_text, size=20, weight='bold', color='black')
axs[1][0].plot(x1, weights_array1[:, 1])
axs1_ylabel_text = axs[1][0].set_ylabel(u'w1', FontProperties=font)
plt.setp(axs1_ylabel_text, size=20, weight='bold', color='black')
axs[2][0].plot(x1, weights_array1[:, 2])
axs2_title_text = axs[2][0].set_title(u'迭代次数', FontProperties=font)
axs2_ylabel_text = axs[2][0].set_ylabel(u'w2', FontProperties=font)
plt.setp(axs2_title_text, size=20, weight='bold', color='black')
plt.setp(axs2_ylabel_text, size=20, weight='bold', color='black')
x2 = np.arange(0, len(weights_array2), 1)
axs[0][1].plot(x2, weights_array2[:, 0])
axs0_title_text = axs[0][1].set_title(u'梯度上升算法,回归系数与迭代次数关系', FontProperties=font)
axs0_ylabel_text = axs[0][1].set_ylabel(u'w0', FontProperties=font)
plt.setp(axs0_title_text, size=20, weight='bold', color='black')
plt.setp(axs0_ylabel_text, size=20, weight='bold', color='black')
axs[1][1].plot(x2, weights_array2[:, 1])
axs1_ylabel_text = axs[1][1].set_ylabel(u'w1', FontProperties=font)
plt.setp(axs1_ylabel_text, size=20, weight='bold', color='black')
axs[2][1].plot(x2, weights_array2[:, 2])
axs2_title_text = axs[2][1].set_title(u'迭代次数', FontProperties=font)
axs2_ylabel_text = axs[2][1].set_ylabel(u'w2', FontProperties=font)
plt.setp(axs2_title_text, size=20, weight='bold', color='black')
plt.setp(axs2_ylabel_text, size=20, weight='bold', color='black')
plt.show()
if __name__ == '__main__':
dataMat, labelMat = loadDataSet()
weights2, weights_array2 = gradAscent(dataMat, labelMat)
weights1, weights_array1 = stocGradAscent1(np.array(dataMat), labelMat)
plotWeights(weights_array1, weights_array2)
import numpy as np
import random
"""
Desc:
sigmoid函数
Parameters:
inX - 数据
Returns:
sigmoid函数
"""
def sigmoid(inX):
return 1.0 / (1 + np.exp(-inX))
"""
Desc:
梯度上升法
Parameters:
dataMath - 数据集
classLabels - 数据标签
Returns:
weights.getA() - 求得的权重数组(最优参数)
weights_array - 每次更新的回归系数
"""
def gradAscent(dataMath, classLabels):
dataMatrix = np.mat(dataMath)
labelMat = np.mat(classLabels).transpose()
m, n = np.shape(dataMatrix)
alpha = 0.01
maxCycles = 500
weights = np.ones((n, 1))
for k in range(maxCycles):
h = sigmoid(dataMatrix * weights)
error = labelMat - h
weights = weights + alpha * dataMatrix.transpose() * error
return weights.getA()
"""
Desc:
改进的随机梯度上升法
Parameters:
dataMatrix - 数据数组
classLabels - 数据标签
numIter - 迭代次数
Returns:
weights - 求得的回归系数数组(最优参数)
"""
def stocGradAscent1(dataMatrix, classLabels, numIter=150):
m, n = np.shape(dataMatrix)
weights = np.ones(n)
for j in range(numIter):
dataIndex = list(range(m))
for i in range(m):
alpha = 4/(1.0+j+i)+0.01
randIndex = int(random.uniform(0, len(dataIndex)))
h = sigmoid(sum(dataMatrix[randIndex] * weights))
error = classLabels[randIndex] - h
weights = weights + alpha * error * dataMatrix[randIndex]
del(dataIndex[randIndex])
return weights
"""
Desc:
用python写的Logistic分类器做预测
Parameters:
None
Returns:
None
"""
def colicTest():
frTrain = open('horseColicTraining.txt')
frTest = open('horseColicTest.txt')
trainingSet = []
trainingLabels = []
for line in frTrain.readlines():
currLine = line.strip().split('\t')
lineArr = []
for i in range(len(currLine) - 1):
lineArr.append(float(currLine[i]))
trainingSet.append(lineArr)
trainingLabels.append(float(currLine[-1]))
trainWeights = gradAscent(np.array(trainingSet), trainingLabels)
errorCount = 0
numTestVect = 0.0
for line in frTest.readlines():
numTestVect += 1.0
currLine = line.strip().split('\t')
lineArr = []
for i in range(len(currLine) - 1):
lineArr.append(float(currLine[i]))
if int(classifyVector(np.array(lineArr), trainWeights[:,0])) != int(currLine[-1]):
errorCount += 1
errorRate = (float(errorCount) / numTestVect) * 100
print("测试集错误率为:%.2f%%" % errorRate)
"""
Desc:
分类函数
Parameters:
inX - 特征向量
weights - 回归系数
Returns:
分类结果
"""
def classifyVector(inX, weights):
prob = sigmoid(sum(inX * weights))
if prob > 0.5:
return 1.0
else:
return 0.0
if __name__ == '__main__':
colicTest()
'''
测试集错误率为:28.36%
'''
from sklearn.linear_model import LogisticRegression
"""
Desc:
使用Sklearn构建Logistic回归分类器
Parameters:
None
Returns:
None
"""
def colicSklearn():
frTrain = open('horseColicTraining.txt')
frTest = open('horseColicTest.txt')
trainingSet = []
trainingLabels = []
testSet = []
testLabels = []
for line in frTrain.readlines():
currLine = line.strip().split('\t')
lineArr = []
for i in range(len(currLine) - 1):
lineArr.append(float(currLine[i]))
trainingSet.append(lineArr)
trainingLabels.append(float(currLine[-1]))
for line in frTest.readlines():
currLine = line.strip().split('\t')
lineArr = []
for i in range(len(currLine) - 1):
lineArr.append(float(currLine[i]))
testSet.append(lineArr)
testLabels.append(float(currLine[-1]))
classifier = LogisticRegression(solver='liblinear', max_iter=10).fit(trainingSet, trainingLabels)
test_accurcy = classifier.score(testSet, testLabels) * 100
print("正确率为:%f%%" % test_accurcy)
if __name__ == '__main__':
colicSklearn()
'''
正确率为:73.134328%
'''
