算法导论——字符串搜索FiniteMachine有限状态机实现

数字逻辑、计组等等我们都遇到过有限状态机，如Moore机，Mealy机。算法中的状态机同样有意思，当面对情况较多的时候，我们通常可以用状态机的思想来编写算法。这也是有限状态机的优秀思想

理论

如何用状态机的思想来解决字符串匹配的问题呢？我想通过一个简单的例子，大家便能够知道其具体做法了。
$给定一个字符集\{a,b,c\}$
$给定一个文本串T=\{a,b,c,a,a,c,a\}$
$给定一个模式串P=\{a,a,c\}$
现在，我们的思想是什么呢？抹去文本串T，对于我们的模式串P，假设我们已经匹配到了q个字符，下一次的输入会有3种情况a,b,c，这三种输入会影响我们已匹配的字符，即会从q状态转移到q’状态。当状态q=3时，就说明我们找到了一个匹配。基于这种思想，我们将以匹配到的字符个数作为我们的状态。下面，给出状态转移表（状态转移方程）

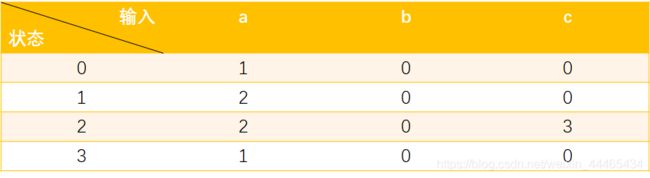
来解释一下这个状态转移表：

• 当状态为0时，说明此时没有匹配的字符。
  • 输入a，因为模式串是{a，a，c}，所以匹配一个字符，状态转移至1；
  • 输入b， 因为模式串是{a，a，c}，所以未匹配字符，状态仍为0；
  • 输入c，因为模式串是{a，a，c}，所以未匹配字符，状态仍为0；
• 当状态为1时，说明此时已有匹配的字符P[1]=‘a’。
  • 输入a，因为模式串是{a，a，c}，加上之前匹配的a，就是’aa’，共匹配两个字符，状态转移至2
  • 输入b， 因为模式串是{a，a，c}，加上之前匹配的a，就是’ab’，所以未匹配字符，状态仍为0；
  • 输入c，因为模式串是{a，a，c}，加上之前匹配的a，就是’ac’，所以未匹配字符，状态仍为0；
    以此类推……

根据我们的状态转移表，我们如何求解呢？
下面考虑$给定的文本串T=\{a,b,c,a,a,c,a\}$
一开始我们的状态是一个都未匹配，q=0

• 文本串输入一个字符’a’，查表知，状态转移至1
• 文本串输入一个字符’b’，查表知，状态转移至0
• 文本串输入一个字符’c’，查表知，状态转移至0
• 文本串输入一个字符’a’，查表知，状态转移至1
• 文本串输入一个字符’a’，查表知，状态转移至2
• 文本串输入一个字符’c’，查表知，状态转移至3, 匹配成功
• ……

这就是有限状态机的基本思想，可见，和数字逻辑设计、计组中的状态机可以说是一毛一样啊有没有。不多BB了，开始实战

实践

Program.cs

using System;
using System.Collections.Generic;

namespace StringMatch
{
    class Program
    {
        static void Main(string[] args)
        {
            
            string T = "Star, I Want to Love with U, I'm so in Love with U";
            string CharacterSet = T;
            string P = "Love with U";



            Console.WriteLine("有限自动机算法");
            InfiniteMachine infiniteMachine = new InfiniteMachine();
            result = infiniteMachine.InfiniteMachineStrategy(T, CharacterSet, P);
            GetResult(result, P, T);

    }
}

FiniteMachine.cs

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;

namespace StringMatch
{
    public class FiniteMachine
    {
        /// 

        /// 状态转移模型
        /// 
        /// 字符集
        /// 模式串
        /// 
        private int[,] StatueTransitionFunction(string CharacterSet, string P)
        {
            int m = P.Length;
            int[,] delta = new int[P.Length + 1, CharacterSet.Length];
            for(int q = 0; q <= m; q++)
            {
                for(int a = 0; a < CharacterSet.Length; a++)
                {
                    /*演算
                    thegma(x):=max{k:P[1,2,...,k]是x的后缀}
                    Delta(q,a) = thegma(Pq+'a')
                    thegma(Pk+'a')即max{k':P[1,2,3,...,k']是(Pq+'a')的后缀}
                    简而言之，就是计算当加入字符'a'后的状态值
                    */
                    delta[q, a] = Thegma(P, q, CharacterSet[a]);

                }
            }
            return delta;
        }

        /// 

        /// 有限状态机求解字符串匹配问题
        /// 
        /// 
        /// 
        /// 
        /// 
        public List<int> FiniteMachineStrategy(string T, string CharacterSet, string P)
        {
            List<int> result = new List<int>();
            int q = 0;
            int m = P.Length;
            int[,] delta = StatueTransitionFunction(CharacterSet, P);
            for(int i = 0; i < T.Length; i++)
            {
                q = delta[q, CharToIndex(T[i], CharacterSet)];
                if(q == m)
                {
                    result.Add(i - m + 1);
                }
            }
            return result;
        }

        private int CharToIndex(char t, string CharacterSet)
        {
            return CharacterSet.ToList().FindIndex(item => item == t );
        }

        /// 

        /// 未优化的Thegma函数
        /// 
        /// 
        /// 
        /// 
        /// 
        private int Thegma(string P, int q, char a)
        {
            List<char> Pq = new List<char>();
            for(int i = 0; i < q; i++)
            {
                Pq.Add(P[i]);
            }
            Pq.Add(a);//Pq+'a'
            int maxK = 0;
            for(int k = 1; k <= Pq.Count && k <= P.Length; k++)
            {
                if(ListToString(Pq).Substring(Pq.Count - k, k) == P.Substring(0, k))
                {
                    maxK = k;
                }
            }
            return maxK;
        }

        private string ListToString(List<char> list)
        {
            StringBuilder stringBuilder = new StringBuilder();
            foreach (char item in list)
            {
                stringBuilder.Append(item);
            }
            return stringBuilder.ToString();
        }
    }
}