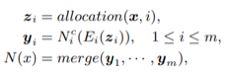人工机器:人工智能中的机器学习方法
人工智能的定义为基于表观的行为定义,即图灵测试,可以形式化为模式识别。智能从知识论的角度分析,归纳明确知识规则构建知识图谱系统形成专家系统,而通过数据获得归纳规则约束参数为机器学习系统,即基于数据的模式识别系统。大量的机器学习模型,可以抽象为特定形式的神经网络,处理输入数据为定长输入或者变长输入。可处理变长数据的NN代表为RNN-循环神经网络。
知识系统应用于现实之前,需要完成ND系统的完备性构造,存在前向链和反向链的使用问题。一个完全性系统,基于前向链使用复合或者单向推理过程(命题推理或者谓词推理),构造ND系统。而对于不完全系统,构造时候需要使用反向链或者归纳方法,机器学习系统是一个使用归纳法完成的观测-假设-归纳系统。
认知与辩证
古老的认知系统已经构建了一个自然关系与人类社会的谚语“天行有常,不为尧存,不为桀亡”,在此,只是断章取义,与古人原义稍有出处,解释为自然基本法则独立于人类社会而运行。
认知,是指人们获得知识或应用知识的过程,或信息加工的过程,这是人的最基本的心理过程。它包括感觉、知觉、记忆、思维、想像和语言等。人脑接受外界输入的信息,经过头脑的加工处理,转换成内在的心理活动,进而支配人的行为,这个过程就是信息加工的过程,也就是认知过程。-百度百科
..............
此外还有诸多经过哲学认可的概念性定义,不接受辩驳,或者根基性反对,文章只是梳理和一个知识阐述过程,可以指正逻辑错误,但概念和定义不接受辩证。
..................................
认知/知识系统要求完备性,矛盾是不应该存在的。哲学的许多问题已经通过科学和数学的方式得到根本性的解决,但仍然有不完备的地方。
语法的完备性与语义的完备性:语义的完备性是不可解决的,语法的完备性是已经证明的。
...................................
知识论:西哲将知识分为两种,先验知识和后验知识。先验意味着仅凭推理得到的知识。(先於经验观察),而不受直接或间接经验(这里经验通常指通过感官对于世界的观察)的影响。后验指其他种类的知识,也就是知识的得来和证实需要借助经验(经验观察之后),也被称作经验性知识。
从历史意义上说,不存在纯粹的先验知识,即不依赖后验知识的先验知识。定理是先验知识,但定理的成立依赖于公理的成立(百科:知识论)。
知识论与哲学系统:哲学(英语:Philosophy,希腊语:Φιλοσοφία),是对基本和普遍之问题的研究。其按其词源有「爱智慧」之意。哲学是有严密逻辑系统的宇宙观,它研究宇宙的性质、宇宙内万事万物演化的总规律、人在宇宙中的位置等等一些很基本的问题。
辩证法:辩证法三大规律,即对立统一规律、量变质变规律、否定之否定规律。这三个辩证法规律在哲学上普遍性达到极限程度。这是黑格尔在《逻辑学》中首先阐述出来的,恩格斯则将它从《逻辑学》中总结和提炼出来,从而使辩证法的规律变得更加清晰了。辩证法规律揭示的全是极限本质之间的联系,是抽象程度最高的产物。
归纳法:归纳推理是一种由个别到一般的推理。由一定程度的关于个别事物的观点过渡到范围较大的观点,由特殊具体的事例推导出一般原理、原则的解释方法。自然界和社会中的一般,都存在于个别、特殊之中,并通过个别而存在。通过观察个别得到共性和一般性原理的过程,为归纳过程。
归纳与演绎:演绎推理(Deductive Reasoning)是由一般到特殊的推理方法。与“归纳法”相对。推论前提与结论之间的联系是必然的,是一种确实性推理。
哲学和数理逻辑
作为系统论可以解析的哲学系统有一个数学基础,为数理逻辑。哲学基本定义在数理逻辑里有一个基本的映射。
数理逻辑的主要分支包括:逻辑演算(包括命题演算和谓词演算)、模型论、证明论、递归论和公理化集合论。古典哲学系统的性质在数理逻辑中得到了形式化解释,而数理逻辑。
数理逻辑的基础设施为命题演算和一阶数理逻辑。一阶逻辑的元逻辑结果为:1.定理的可靠性,一阶逻辑内的定理在论域内是完全有效的;2.一致性,逻辑定理与其规约(全称量词约去)的命题演算是一致的;3.完全性,一阶逻辑下凡是有效的公式都是定理,都可以由公理证明;4.紧致性,公式集г是一致的,当且仅当它的每一有穷子集是一致的。
从定理到命题的规约过程为归纳,从命题到定理的过程叫演绎。归纳法企图使用论域规约到一般概念即全域,演绎是命题展开为全域定理的过程。
归纳与演绎在数理逻辑中的数学定义为:..............................
归纳法既然是从论域到全域的规约过程,隐含着不能覆盖全域,天然的具有一定概率的错误情况。
贝叶斯错误率:贝叶斯决策理论是主观贝叶斯派归纳理论的重要组成部分。 贝叶斯决策就是在不完全情报下,对部分未知的状态用主观概率估计,然后用贝叶斯公式对发生概率进行修正,最后再利用期望值和修正概率做出最优决策。
对于任何给定问题,可以通过似然率测试决策规则得到最小的错误概率。这个错误概率称为贝叶斯错误率,且是所有分类器中可以得到的最好结果。最小化错误概率的决策规则就是最大化后验概率判据。
归纳过程是一阶谓词逻辑定理命题化的过程,是一个天然的贝叶斯判定过程,归纳法天然具有错误率,这个错误率的最好极限也是贝叶斯错误率。
全域和论域
作为集合论乃至整个数学系统基础的数理逻辑,根据命题公式和谓词逻辑提出的全域和论域概念,最初是解决古老迂腐的哲学家苏格拉底的必死命题而提出的。
命题逻辑建立在全域概念上,而谓词逻辑建立在论域概念上,论域可以是全域或者全域的子集。
包含统计学在内,大多数学科基础的的基础理论与数理逻辑是同构的,机器学习理论有深刻的统计学基础理论支撑。
统计学中,对应论域的概念为采样空间,而全域的概念为样本空间,采样空间为可观测空间又称随机事件,即样本空间中可以被观察到的样本所覆盖的空间。
机器学习的数理逻辑解释为在全域的子集特定的论域上,使用归纳方法归纳出命题,得到模型即命题集合的方法。
PAC学习理论:
Hoeffding不等式:https://blog.csdn.net/wangjianguobj/article/details/57413819
本小节结论:只要样本数量m大于公式(3)中的M,就能保证模型在当前条件下是PAC可学习的。
VC维理论:一个更紧的条件
先说一下什么是紧。简单的讲,紧的意思就是恰好满足条件。开集表示局部,而紧性则是可以将局部的性质推广到全局。在度量空间中,紧性等价于自列紧性。
为了保证PAC可学习,根据公式(3),需要样本数量大于等于M。M此值越小,PAC条件就越有可能达到。那么有没有比M更紧也就是更小的值呢?这就引出了VC维理论。
论域的流动性-时间维
人不能两次踏入同一条河流。
模型论与证明论
数学公理化,归纳方法的完备性,语义系统的遍历性质。
数学公理化推进的最关键标志性事件是1920~1923年间,希尔伯特推动的“希尔伯特计划”。这个计划的主要目标,是为全部的数学提供一个安全的理论基础。这个计划对数学公理化提出了如下要求:
形式化:形式化是希尔伯特提出来的一个关键思想,意思是,所有数学应该使用用统一的、严格的、无意义的、形式化的语言来表述,并且按照一套严格的、基础的逻辑规则来推演。
完备性:形式化之后,数学里所有的真命题都可以通过上述规则被证明。
一致性:运用这一套形式化的表达和规则,不可能推导出矛盾。
保守性:这是针对形式化而言的,即如果赋予一些形式化的表达以含义(希尔伯特将这称为元数学),并由此证明了某些结论,那么必须保证即使不赋予这些含义,依然可以证明同样的结论。
确定性:可以通过一个算法来确定每一个形式化的命题是真还是假。
对于修炼完成了“哥德尔不完备定理”第一重神功的读者来说,应该会看出上述“希尔伯特计划”是有问题的。没错,之所以我们比大数学家希尔伯特还要目光如炬,是因为我们站在哥德尔这个巨人的肩膀上!要知道,在哥德尔的论文发表之前,甚至是发表之后的一段时间,主流数学家、逻辑学家们仍然认为希尔伯特计划毫无疑问是正确的,问题只不过是如何给出证明罢了。
文章:哥德尔不完备性定理在说些什么-二?
证明论(Proof theory),是数理逻辑的一个分支,它将数学证明表达为形式化的数学客体,从而通过数学技术来简化对他们的分析。证明通常用归纳式地定义的数据结构来表达,例如链表,盒链表,或者树,它们根据逻辑系统的公理和推理规则构造。因此,证明论本质上是语法逻辑,和本质上是语义学的模型论形相反。和模型论,公理化集合论,以及递归论一起,证明论被称为数学基础的四大支柱之一。
哥德尔完备性定理是数理逻辑中重要的定理,在1929年由库尔特·哥德尔首先证明。它的最熟知的形式声称在一阶谓词演算中所有逻辑上有效的公式都是可以证明的。
数学上,模型论是研究数学对象用集合论的属于表示数学概念的学科,或者是研究数学系统的组成模型的学科。它假定存在一些预先存在的数学对象,然后研究,给定这些对象、操作或者对象间的关系、以及一组公理时,什么可以被证明,如何证明的问题。
哥德尔完备性定理表明理论有一个模型当且仅当它是自洽的,也就是说没有矛盾可以被该理论所证明。这是模型论的中心,因为它使得我们能够通过检视模型回答关于理论的问题,反之亦然。不要把完备定理和完备理论的概念混淆。一个完备的理论是包含每个句子或其否命题的理论。重要的是,一个完备的自洽理论可以通过扩展一个自洽的理论得到。
哥德尔在论文中明确提到,这种构造思路是来源于两个有名的悖论——理查德悖论(Richard-antinomy)和说谎者悖论(liar-antinomy),后者就是我们最前面说到的“这句话是谎话”的悖论,而前者则与哥德尔的构造有类似之处,感兴趣的读者可以自行了解。
哥德尔证明的一个关键点,就是把“真”、“假”与“可证明”及“不可证明”区分开来了。这里谈到的可证明与否都是指在PM体系之内。我们日常生活与工作中,经常把“真假”与“是否可证明”等同起来,认为“真⇔可证明”,“假⇔不可证明”。其实,“真假”与“是否可证明”的严格关系应该是“可证明⇒真”、“假⇒不可证明”,但是它们的逆命题却不成立,也就是说“真命题未必可证明”,同时“不可证明的也未必就是假命题”。
文章:哥德尔不完备性定理在说些什么-三?
而哥德尔的不完备性定理,则证明了语义系统的不完备性。
第一定理:任意一个包含一阶谓词逻辑与初等数论的形式系统,都存在一个命题,它在这个系统中既不能被证明为真,也不能被证明为否。
第二定理:如果系统S含有初等数论,当S无矛盾时,它的无矛盾性不可能在S内证明。
缸中之脑
哲学的第一悖论为“缸中之脑”,没有根基是一个完备感知系统的根基。在计算机基础科学中,这个论题演化为“丘奇-图灵问题”,在数学与逻辑学中,这个问题为哥德尔的不完备性定理。
即没有一个基础是所有一切的基础,这个理论动摇了语义系统的根基。
假设与证明
从最基本的知识理论开始,知识的构建即存在一个“假设”与“证明”的过程。对于自然科学文盲的文科生来说,每一个古老的哲学问题都让他们一筹莫展,在逻辑完备的过程中耗尽所有聪明。其中最悲惨的不是“缸中之脑”的不可描述之解释,而是知识论固有的“空地上的牛奶”问题。
这个理论表明了语法系统的缺陷;
空地上的牛奶,它描述的是,一个农民担心自己的获奖的奶牛走丢了。这时送奶工到了农场,他告诉农民不要担心,因为他看到那头奶牛在附近的一块空地上。虽然农民很相信送奶工,但他还是亲自看了看,他看到了熟悉的黑白相间的形状并感到很满意。过了一会,送奶工到那块空地上再次确认。那头奶牛确实在那,但它躲在树林里,而且空地上还有一大张黑白相间的纸缠在树上,很明显,农民把这张纸错当成自己的奶牛了。于是问题出现了,虽然奶牛一直都在空地上,但农民说自己知道奶牛在空地上时是否正确?
空地上的奶牛(The Cow in the field)最初是被Edmund Gettier用来批判主流上作为知识的定义的JTB(justified true belief)理论,即当人们相信一件事时,它就成为了知识;这件事在事实上是真的,并且人们有可以验证的理由相信它。在这个实验中,农民相信奶牛在空地上,且被送奶工的证词和他自己对于空地上的黑白相间物的观察所证实。而且经过送奶工后来的证实,这件事也是真实的。尽管如此,农民并没有真正的知道奶牛在那儿,因为他认为奶牛在那儿的推导是建立在错误的前提上的。Gettier利用这个实验和其他一些例子,解释了将知识定义为JTB的理论需要修正。
空地上的牛奶问题,设计了归纳的可信度问题,或许这个例子不能很好的描述假设与证明的问题。真正地假设与证明的问题,可以使用统计理论进行定理化的证明,涉及采样理论和观测系统概念。
模型
以哲学的本质-完备性作为要求,使用实验的方法进行观测样本即论域,进行假设,并使用科学方法进行实验(扩充论域,验证是否准确),即证明,构建-修改-添加知识规则,是知识系统构建的一般过程。这个基本过程推演出了无数条剥离数学的哲学方法,如矛盾与统一、否定之自否等等一系列马恩列斯毛的科学社会主义基本方法论的一些方法。
完备性并非总是可达,因此权衡出论域的泛化空间准确度,即泛化性能。
观测、归纳、验证在可以接受的性能内形成的一定可信度的规则集合,被称为“模型”。模型的定义包含了样本集-论域、假设空间以及可扩充论域的泛化性能。
参数与超参数简介
我们把一个可以处理固定映射的参数模型分为几个层次,模型结构和模型参数。基于数据的模式识别所称为“训练”的过程,是固定模型之后对模型使用数据进行调整训练的过程为参数寻优过程,目的为使模型符合ε学习,完成模型优化。
参数与超参数,在固定模型的参数模型中,固定模型的一般约束参数为超参数,“训练过程”使用数据优化改变的参数为参数,即对于参数模型训练过程是在超参数的约束下优化参数的过程。
对于特定场景的模型,超参数一般固定模型的结构,而参数则意味着固定了固定结构的映射属性。
从泛函分析的角度来看,模型的一类结构表示了一类算子,模型的超参数为算子的数值定义域。而模型的参数,则率属于函数模型的数值定义域。
以传统的机器学习方法,简单的多元一次线性回归 为例,多元一次线性为模型的结构,选定的元数n为模型的超参数,模型的ai为模型的参数。
以泛函的角度分析,多元一次线性回归为压缩算子y=L(Rx) 的一个定义,其中n为y=L(Rx) 的一个定义,代表Rn空间的一个子集。
CNN模型的超参数和参数
以图像处理典型的CNN分类方法为例,CNN结构为模型的结构。CNN结构比较复杂,以普遍使用最简单的LeNet为例,不包含输入和输出,LeNet有七层,分别为C1、S2、C3、S4、C5、F6,最后一层为判别函数。
而每一层的结构分别为:
Input Layer:1*32*32图像
Conv1 Layer:包含6个卷积核,kernal size:5*5,parameters:(5*5+1)*6=156个
Subsampling Layer:average pooling,size:2*2
Activation Function:sigmoid
Conv3 Layer:包含16个卷积核,kernal size:5*5 ->16个Feature Map
Subsampling4 Layer:average pooling,size:2*2
Conv5 Layer:包含120个卷积核,kernal size:5*5
Fully Connected Layer6:Activation Function:sigmoid
Output Layer:Gaussian connection..。
每一层的函数形式都是固定了,因此构建了一个固定的网络结构。Conv1层使用6个5*5的卷积核的函数结构,其中6个为层的结构,5*5为卷积函数的超参数,而每个5*5的卷积核里面的值为参数。
CNN的机器学习过程,是固定了CNN的模型参数,使用数据训练LeNetCNN的过程,即使使用数据和反传算法优化每一个卷积核参数的过程。
而每一个卷积核的值,即是卷积函数的参数,也是CNN的特征提取器,因此CNN方法也称为“特征学习”。特征学习和模式识别器的参数训练,皆为参数学习。
结构搜索与泛函
机器学习方法存在着固定场景中寻找特定模型固定结构的参数学习与固定场景的特定模型的结构学习。
哪个结构才是最优的呢?在自动化结构搜索之前,模型的结构搜索是由人类专家完成,无数次的模型假设和实验,无数次的欠拟合和过拟合的博弈,最终在图像识别比赛中胜出的ALexNet是辛顿和其学生多年努力搜索的结果,这一结构凝结了大量的专家知识,对于图像结构分类的知识描述映射为CNN网络的结构形式,是辛顿团队人脑搜索多年取得的成果。而这个成果对于ImageNet的图像分类是否过拟合或者欠拟合,都在后续时间内反复斟酌。
属性集,映射对参数集,定义域搜索约束在向量空间。而模型结果的搜索,超参数的寻优过程,进一步扩展到张量空间。在向量空间内一个正交属性为一个维度,量化符号为“维度”,向量空间为一阶张量。张量的量化符号为“阶”。
张量与空间
张量(Tensor)是一个定义在的一些向量空间和一些对偶空间的笛卡儿积上的多重线性映射,其坐标是|n|维空间内,有|n|个分量的一种量, 其中每个分量都是坐标的函数, 而在坐标变换时,这些分量也依照某些规则作线性变换。r 称为该张量的秩或阶(与矩阵的秩和阶均无关系)。
张量的阶与维度................
在同构的意义下,第零阶张量 (r = 0) 为标量 (Scalar),第一阶张量 (r = 1) 为向量 (Vector), 第二阶张量 (r = 2) 则成为矩阵 (Matrix)。例如,对于3维空间,r=1时的张量为此向量:(x,y,z)。由于变换方式的不同,张量分成协变张量 (Covariant Tensor,指标在下者)、逆变张量 (Contravariant Tensor,指标在上者)、 混合张量 (指标在上和指标在下两者都有) 三类。
在数学里,张量是一种几何实体,或者说广义上的“数量”。张量概念包括标量、向量和线性算子。张量可以用坐标系统来表达,记作标量的数组,但它是定义为“不依赖于参照系的选择的”。张量在物理和工程学中很重要。例如在扩散张量成像中,表达器官对于水的在各个方向的微分透性的张量可以用来产生大脑的扫描图。可能最重要的工程上的例子就是应力张量和应变张量了,它们都是二阶张量,对于一般线性材料他们之间的关系由一个四阶弹性张量来决定。
虽然张量可以用分量的多维数组来表示,张量理论存在的意义在于进一步说明把一个数量称为张量的涵义,而不仅仅是说它需要一定数量的有指标索引的分量。特别是,在坐标转换时,张量的分量值遵守一定的变换法则。
张量的抽象理论是线性代数分支,现在叫做多重线性代数。(摘自于百度百科)
拓扑空间与线性空间
拓扑空间与拓扑学
拓扑空间是一个集合 X和其上定义的拓扑结构组成的二元组。X的元素 x通常称为拓扑空间 的点。而拓扑结构一词涵盖了开集,闭集,邻域,开核,闭包,导集,滤子等若干概念。从这些概念出发,可给拓扑空间作出若干种等价的定义。 [2]
拓扑空间作为对象,连续映射作为态射,构成了拓扑空间范畴,它是数学中的一个基础性的范畴。试图通过不变量来对这个范畴进行分类的想法,激发和产生了整个领域的研究工作,包括同伦论、同调论和K-理论。
设是一个集合,是一些的子集构成的族,则(,)被称为一个拓扑空间,如果下面的性质成立:
1.空集和属于,
2.中任意多个元素的并仍属于,
3.中有限个元素的交仍属于。
这时,中的元素成为点(point),中的元素成为开集(open set)。我们也称是上的一个拓扑。
拓扑空间有独立研究的价值,研究拓扑空间的数学分支称为拓扑学。
豪斯多夫分离公理:(T2分离公理) 空间内任何两个不同的点都各有邻域互不相交。
豪斯多夫空间与数学分析
在拓扑学和相关的数学分支中,豪斯多夫空间、分离空间或T2 空间是其中的点都“由邻域分离”的拓扑空间。在众多可施加在拓扑空间上的分离公理中,“豪斯多夫条件”是最常使用和讨论的。它蕴涵了序列、网和滤子的极限的唯一性。豪斯多夫得名于拓扑学的创立者之一费利克斯·豪斯多夫。豪斯多夫最初的拓扑空间定义把豪斯多夫条件包括为公理。
在数学分析所遇到的几乎所有空间都是豪斯多夫空间。
度量空间与泛函分析
度量空间(Metric Space),在数学中是指一个集合,并且该集合中的任意元素之间的距离是可定义的。是任一元素可度量的拓扑空间。
在度量空间中,紧性、可数紧性、序列紧性、子集紧性是一致的。可分性、遗传可分性、第二可数性、林德勒夫性是一致的。度量空间必满足第一可数公理,是豪斯多夫空间,完全正规空间,仿紧空间。伪度量空间满足第一可数公理,但一般不是豪斯多夫空间。
函数空间与向量丛
处理分析问题时,根据具体情况需要可以引入种种函数空间。例如,考虑定义于闭区间[0,1]上的一切连续实值函数的集合,就可以定义两个函数ƒ 和g的距离为
度量空间
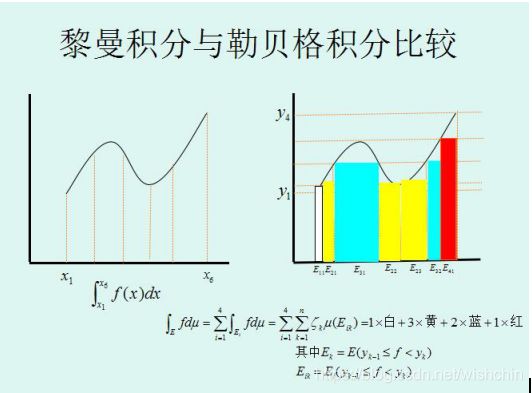
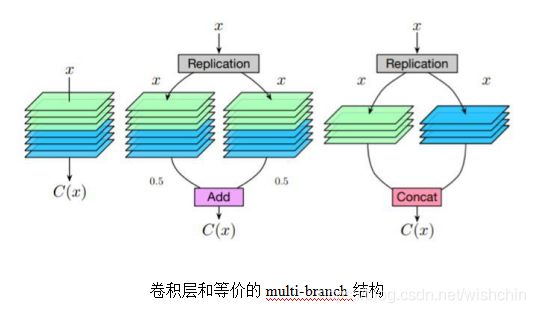
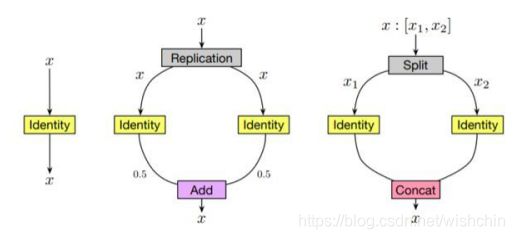
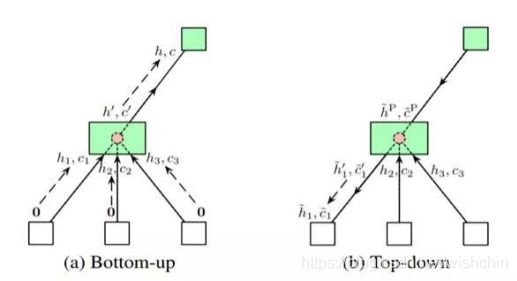
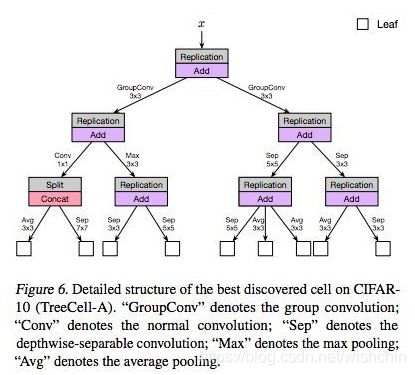
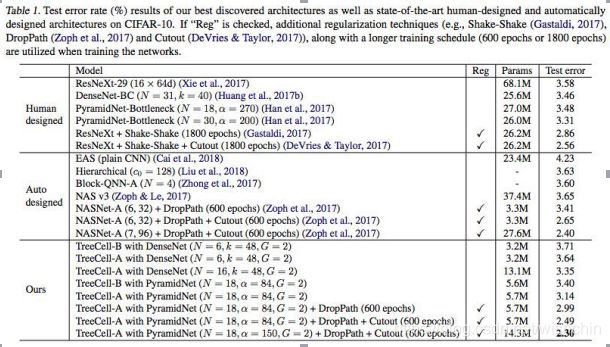
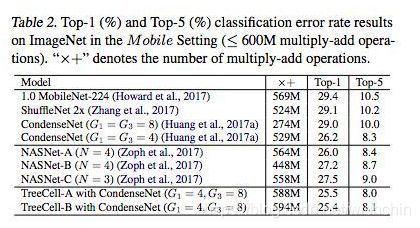
对于度量空间X,可以利用它的度量d 引进一个拓扑结构,其基的元就是所有的开球B(x,r)={y∈X|d(x,y) 例如,对于实数集R,d(x,y)=|x-y|与度量空间 就产生同一个拓扑结构。度量不是拓扑概念。(摘自于百科:度量空间) 向量丛是一个几何构造,对于拓扑空间(或流形,或代数簇)的每一点用互相兼容的方式附上一个向量空间,所用这些向量空间"粘起来"就构成了一个新的拓扑空间(或流形,或代数簇)。其定义阐述了向量丛的一般性质(百科:向量丛)。 线性空间与泛函分析 定义了距离后,我们再加上线性结构,如向量的加法、数乘,使其满足加法的交换律、结合律、零元、负元;数乘的交换律、单位一;数乘与加法的结合律(两个)共八点要求,从而形成一个线性空间,这个线性空间就是向量空间。 向量空间又称线性空间,是线性代数的中心内容和基本概念之一。在解析几何里引入向量概念后,使许多问题的处理变得更为简洁和清晰,在此基础上的进一步抽象化,形成了与域相联系的向量空间概念。譬如,实系数多项式的集合在定义适当的运算后构成向量空间,在代数上处理是方便的。单变元实函数的集合在定义适当的运算后,也构成向量空间,研究此类函数向量空间的数学分支称为泛函分析。 范数与距离 在向量空间中,我们定义了范数的概念,表示某点到空间零点的距离: 将范数与距离比较,可知,范数比距离多了一个条件2,数乘的运算,表明其是一个强化了的距离概念。范数与距离的关系可以类似理解为与红富士苹果与苹果的关系。 文章:范数. 接下来对范数和距离进行扩展,形成如下: 下面在已经构成的线性赋范空间上继续扩展,添加内积运算,使空间中有角的概念,形成如下: 继续在内积空间上扩展,使得内积空间满足完备性,形成希尔伯特空间如下: 此外,前面提到的赋范空间,使其满足完备性,扩展形成巴拿赫空间如下: 以上均是在距离的概念上进行添加约束形成的,递增关系如下: 顺便提以下,对距离进行弱化,保留距离的极限和连续概念,就形成拓扑的概念。 文章:稀疏表达-向量、矩阵与张量(中)-0、1、2范数与RPCA 函数与对偶 1914年豪斯道夫(F.Hausdorff)在《集合论纲要》中用不明确的概念“序偶”来定义函数,其避开了意义不明确的“变量”、“对应”概念。库拉托夫斯基(Kuratowski)于1921年用集合概念来定义“序偶”使豪斯道夫的定义很严谨了。 1930 年新的现代函数定义为“若对集合M的任意元素x,总有集合N确定的元素y与之对应,则称在集合M上定义一个函数,记为f。元素x称为自变量,元素y称为因变量” [1] 。 近代定义 设A,B是非空的数集,如果按照某种确定的对应关系f,使对于集合A中的任意一个数x,在集合B中都有唯一确定的数和它对应,那么就称映射为从集合A到集合B的一个函数,记作或。 其中x叫作自变量,叫做x的函数,集合叫做函数的定义域,与x对应的y叫做函数值,函数值的集合叫做函数的值域,叫做对应法则。其中,定义域、值域和对应法则被称为函数三要素。 定义域,值域,对应法则称为函数的三要素。一般书写为。若省略定义域,一般是指使函数有意义的集合 [1] 。 数学中,函数空间指的是从集合 X 到集合 Y 的给定种类的函数的集合。其叫做空间的原因是在很多应用中,它是拓扑空间或向量空间或这二者。 现代分析学的一般方法在于视Ω为拓扑空间或测度空间又以问题的需要规定类中映射(即函数):Ω→A满足的条件,诸如连续性、有界性、可测性、可微性、可积性等; 从几何学、拓扑学及代数学的角度,对X一方面赋与关于加法与数量乘法的封闭性,这里加法为:ƒ∈X,g∈X→ƒ+g∈X,(ƒ+g)(x)=ƒ(x)+ g(x),对x∈Ω;数量乘法为:ƒ∈X,λ∈A→λƒ∈X,(λƒ)(x)=λƒ(x),对x∈Ω(即X对通常函数的线性运算封闭);另一方面使之成为拓扑空间,且两方面又满足一定的要求(例如线性运算关于拓扑是连续的等)。这样,函数空间X通常也是拓扑线性空间。 由原始数的集合到函数集合,扩展出一些列基于函数的算子定义:测度、可积、可微、收敛等一般意义(百科:函数空间)。 以多项式函数回归模型:y=F(x) = ax+ bx^2 + cx^3 +d为例,多项式函数从定义域Rx到值域Ry的函数空间是连续的,且可测、可积可微、可学习。 对于有参数机器学习模型,常见的回归模型(Logistics回归、SVM等)和神经网络模型(回归模型的非线性组合),都是可测可积可微可学习的。 函数积分与实分析 文章:为什么勒贝格积分比黎曼积分强?文风很西化。 黎曼积分和连续函数 柯西(Cauchy)为分析的发展提供了一种严密的语言,但是他并没有解决微积分的全部问题。在19世纪的时候,分析的世界仍然有着一些挥之不去的乌云。而其中最重要的一个没有解决的是“函数是否可积的问题”。我们在现在的微积分课本中学到的那种通过“无限分割区间,取矩阵面积和的极限”的积分,是大约在1850年由黎曼(Riemann)提出的,叫做黎曼积分。但是,什么函数存在黎曼积分呢(黎曼可积)?数学家们很早就证明了,定义在闭区间内的连续函数是黎曼可积的。可是,这样的结果并不令人满意,工程师们需要对分段连续函数的函数积分。 勒贝格积分和测度函数 测度是定义在X∗X上的函数,记为d(x,y)其中x,y∈X,并且满足: 1. d(x,x)=0 2. x≠y时,d(x,y)>0 3. d(x,y)=d(y,x) 4. d(x,y)≤d(x,y)+d(y,z)(三角不等式)。文章:范数、测度和距离.此文总结的非常详细。 测度与范数的区别:测度对应的集合可以是一般的集合,范数对应的集合必须有算术结构 ;如果d(x,y)是向量空间X上的测度,并且满足平移不变性和齐次性,那么这个d(x,0就是某种范数;反之,如果∣∣x∣∣是范数,那么d(x,y)=∣∣x−y∣∣一定是测度。 文章:测度理论简介.大多数的哲学问题都已经被基础数学解决了。 勒贝格在1901年描述勒他的测度,随后在第二年他描述了勒贝格积分。二者都是作为他在1902年的博士论文的一部分发表的。勒贝格测度是赋予欧几里得空间的子集一个长度、面积、或者体积的标准方法。它广泛应用于实分析,特别是用于定义勒贝格积分。可以赋予一个体积的集合被称为勒贝格可测;勒贝格可测集A的体积或者说测度记作λ(A)。 定义了测度的可测空间为测度空间,勒贝格积分把积分运算扩展到任何测度空间中。广义地说是相对于一个测度而定义的函数积分。狭义则是指相对于勒贝格测度在实直线或者更高维数的欧氏空间的一个子集中定义的函数的积分。 勒贝格的博士论文《积分,长度与面积》建立了测度论和积分论,使一些原先在黎曼意义下不可积的函数按勒贝格的意义变得可积了,可以重建微积分基本定理。基于测度论和积分论构建了数学的实变函数论。人们常把勒贝格以前的分析学称为经典分析,而把以由勒贝格积分引出的实变函数论为基础而开拓出来的分析学称为现代分析(百科)。 从直观上看,作为两个描述积分的不同理论,勒贝格积分跟黎曼积分最明显的一个区别是:黎曼积分是对定义域进行划分的,勒贝格积分是对值域进行划分的。勒贝格积分的精髓是证明了函数的不连续点集的测度是零,这样就把黎曼积分不可积的问题解决了。 对于直观上值域可数分割的勒贝格积分,因为用了可数分割,勒贝格积分天生具有可数可加性,而相应的,黎曼积分只具有有限可加性。 此文:黎曼积分与勒贝格积分中,阐述简明直观。这两种积分其实都是加法,但使用的手法不同,用数钱来比较,比如总计有100元,由硬币和纸币组成,黎曼积分采用的是闷头数的方式,遇到硬币算硬币, 纸币算纸币,反正最后也能够数出来正确的结果,勒贝格积分采用另外一种数法,将币种归类,看看10元有几张,20元有几张,1元硬币有多少,也就是说使用5X10+2X20+1X10=100的方式。勒贝格积分的精髓是证明了函数的不连续点集的测度是零,这样就把黎曼积分不可积的问题解决了。 函数值域扩展 通俗地讲,Ax=y的基础解系构成的线性空间,就是这个线性变换的核而值域是Ax取遍所有向量x后的解集。 对于值域扩展的ML模型,泛化理论和PAC学习理论不再对此有任何指导意义。扩充值域的基础前提是同时扩充定义域且新的映射关系与原始模型相同或者相近。 具体方法:? PAC可学习 可积函数是存在积分的函数。除非特别指明,一般积分是指勒贝格积分;否则,称函数为"黎曼可积"(也即黎曼积分存在),或者"Henstock-Kurzweil可积"。在数学分析里,可积分的要求为函数有有限个间断点即可以,在实变函数分析里,要求会更严格(百科:可积函数)勒贝格可积分。 黎曼可积具有乘积、绝对值和复合可积的性质。 在微积分学中,可微函数是指那些在定义域中所有点都存在导数的函数。可微函数的图像在定义域内的每一点上必存在非垂直切线。因此,可微函数的图像是相对光滑的,没有间断点、尖点或任何有垂直切线的点。 机器学习可微函数模型是机器学习参数模型可学习的必要条件。机器学习模型构建学习过程是重建假设并加以检验的一般科学实验过程,其基本理论为PAC可学习理论。机器学习特定的模型可以求得解析解,只应对于线性非共线模型参数个数与 样本个数一致的情况下,但此种情况一般在现实ML中很少出现。大多数ML模型遵从了PAC学习理论,学习过程使用数学优化方法,连续优化的基本前提则是函数的可微性。 特殊函数:连续不可积函数,魏尔斯特拉斯函数连续,但在任一点都不可导、不可微。科学实验建立的数学模型,大部分连续函数是可微的,而在纯数学领域,巴拿赫声称可微函数在所有函数构成的集合中却是少数(百科:可微函数)。 多元函数的可微性需要保证一个函数在某点的邻域内所有偏导数存在且连续,偏导数都存在单独不能保证函数在该点可微。 优化方法-变分法 是处理函数的数学领域,和处理数的函数的普通微积分相对。它最终寻求的是极值函数:它们使得泛函取得极大或极小值。 变分法起源于一些具体的物理学问题,最终由数学家研究解决。有些曲线上的经典问题采用这种形式表达:一个例子是最速降线,在重力作用下一个粒子沿着该路径可以在最短时间从点A到达不直接在它底下的一点B。在所有从A到B的曲线中必须极小化代表下降时间的表达式。 ...... 变分法概念与寻常分析中的微分概念很为类似,但所联系的不是x的变化,而是函数y(x)的变化。如果函数y(x)使U(y)达其极值,则U的变分δU变为0。 最小二乘法与梯度下降法 最小二乘法的目标:求误差的最小平方和,对应有两种:线性和非线性。线性最小二乘法的解释闭式解即x=(ATA)-1ATb,而非线性最小二乘法没有闭式解,通常只能使用迭代搜索方法求解。 张量分析是微分几何中研究张量场的微分运算的一个分支。张量分析是用共变微分表示各种几何量和微分算子性质的运算方法,可以看作是微分流形上的“微分法”,是研究流形上的几何和分析的一种重要工具。 [1] 摘自于百度百科。 多重线性函数 记张量积的数学记号为 ⊗。文章:https://blog.csdn.net/lanchunhui/article/details/65439890 使用了参数模型或者非参数模型的机器学习系统,不是传统意义上的专家系统,依然是一个严重依赖于专家的系统。 专家系统给出了知识节点和规则,使用粒度描述准确性,依靠分解粒度解决矛盾,并反馈知识和推理规则更新。专家系统与机器学习有本质区别,但从机器学习的角度看,专家系统是一个给出了规则/函数又给了函数参数的学习模型,其直接影响是泛化性能极差,容易导致矛盾。这样,每一个专家系统的更新都涉及到知识节点(规则参数)的分解重构,形式上等价于函数复合化。 机器学习系统设计也遵循了模式识别的一般构架与过程。一般在特定或者广泛的应用领域,先给出目标/评价函数,以期待完成预期的结果。再依据目标/评价函数设计满足目标函数的规则系统/数学模型,以期待能完成目标函数所要求的功能。而应对与每个领域,由实体到数学模型的转化,产生了一个特征描述的专家过程,把领域实体表示为学习系统可以接受的输入数据。 机器学习划分出的非监督学习与监督学习,在于是否使用了示例来指导数学模型的优化过程。监督学习给出了形式化的目标函数,形式化的数学模型,形式化的特征提取过程,并且给出了同伦映射空间模型参数的一些阈值确界,学习过程是通过阈值确界通过目标函数约束来优化数学模型的过程。非监督学习没有给出模型参数阈值,但依然有形式化的目标函数,形式化的数学模型和形式化的特征提取过程,主要通过目标函数和数学模型精细结构调整来达到预期目标。 传统的机器学习系统是一个模型逐渐优化的学习系统,学习的终极目标是收敛到一个最优解-模型的最优参数,期待是确定的数学模型。传统的ML系统方法期待模型直接学习到模式的空间结构,并得到空间结构的等价模型映射,相对于任意模型,学习到的模型是e精度最优的,即是e精度最接近的,这就意味着最大的准确率和最大的泛化性能。 跨越到连接主义的范畴,强化学习是一个反馈式学习系统,其期待是一个不断根据反馈进行优化的模型,并非一次成型。 reinforcement learning-RL又称为评价学习,在传统ML领域不存在此种概念,接近于在线弱监督学习。在连接主义学习中,ML划分为监督学习、非监督学习、强化学习RL。 在机器学习学科中,机器学习模型的建立需要摆脱由专家人工构建的过程,完成自动模型搜索,因此引入强化学习概念。通过设计适当的评价模型,从一个模型开始,根据评价模型指导,自动搜索更优的机器学习模型。近期的CNN结构搜索方法使用了被动强化学习的思想,使用固有的策略,在样本空间完全可知状态下,通过评价模型进行评价反馈,在机器学习模型空间中搜索最优模型,而不仅仅是更新固定模型的参数。 缺陷:寻找最优模型的最优参数依然是一个概率过程,RL还不能对模型的泛化性能保证,不能避免过拟合。过拟合的避免依然需要遍历级别的样本空间。 LeNet是第一个成功的手写阿拉伯数字识别模型,ALexNet是第一个成功的ImageNet图像识别模型,从0-1一般由专家构建。而后期模型不断的发展,严重依赖了一种模型搜索方法:迁移学习-EnforceLearning:迁移学习-监督训练与非监督训练。迁移学习使用一个初始化结构开始,人类专家,通过特定规则扩充维度或者逐步搜索构建新的结构,使模型扩大到更大的论域。 从一个初始化的AlexNet结构,不断得搜索,取得了CNN在图像处理模式识别的长足进步与辉煌。AlexNet-GoogleLeNet-.... .....................................................................................希望找到不依赖于专家的模型探索方法................它需要一系列的方法论,这就引发了由方法论引导创建规则,再有规则创建模型的领域.................................... 作为归纳系统的深度学习。 深度学习以“数据驱动”范式颠覆了“人造特征”范式,完成“特征学习”,这是一个重大的进步。但与此同时,它自己又陷入了一个“人造结构”窠臼中。06年hinton教授发表在nature上的最初的论文,多层压缩映射。给出的深度学习的方案是无监督学习获取网络结构,之后再通过有监督学习优化参数,DNN网络的引爆点恰恰是结构学习。大量利用未标记数据学习网络结构是深度学习最初的构想。 但无论Hinton教授组最初设计的AlexNet,还是后来的VGG,GoogLeNet,ResNet等等,都是富有经验的专家人工设计出来的。给定一个新问题,到底什么样的网络结构是最佳的(如多少卷积层)却不得而知,这在一定程度上阻碍了深度学习在更多智能任务上的普及和应用。因此,同时学习网络结构和网络参数是一个值得大力关注的研究方向。 而2006年Hinton教授等人倡导的却恰恰是利用无监督学习来对深层神经网络进行预训练。利用超量的数据学习网络结构是一个更耗费时间和计算能力的事情。此后,特别是DCNN兴起之后,无监督的预训练似乎已经被很多研究者所抛弃(特别是在CV领域)。 直接从大量无监督数据中学习模型确实是非常困难的,即便是人这部“机器”,也有“狼孩”的例子警告我们“无师自通”似乎是不现实的。但“少量有导师数据+大量无导师数据”的弱监督模式也许是更值得大力研究的。 Hinton教授的Auto-Coder/Decoder方法,使用了SparseCoding概念,使用压缩/重建映射的思想通过学习RBM 生成描述 隐藏元。Auto- Coder给出了方向和范围两方面的映射,使用大数据和反向重建思想自动寻找数据本身的稀疏性,仍需要遍历级别的无标签样本。 原始DNN的Auto-Coder/Decoder方法是一种逐层结果反馈驱动的方法,模型率属于NN的层状结构。 VGGNet探索了卷积神经网络的深度与其性能之间的关系,通过反复堆叠3*3的小型卷积核和2*2的最大池化层(最小核和最小池化层),VGGNet成功地构筑了16~19层深的卷积神经网络。获得ImageNet2014年亚军(VGGNet,top-5错误率7.3%,19层神经网络)。 Google Inception Net首次出现在ILSVRC 2014的比赛中(和VGGNet同年),就以较大优势取得了第一名。那届比赛中的Inception Net通常被称为Inception V1,它最大的特点是控制了计算量和参数量的同时,获得了非常好的分类性能——top-5错误率6.67%,只有AlexNet的一半不到。Inception V1中精心设计的Inception Module提高了参数的利用效率。 上图为Inception结构和ResNet基元结构 VGG结构和INception结构、ResNet基元结构的出现,验证了通过反复堆叠小型inception结构可以构建大型CNN网络,而构建过程可以通过特定的规则自动完成,这就引出了CNN结构搜索即结构学习的思路。 Neural Architecture Search With Reinforcement Learning 1611.01578。谷歌推出的NASNet架构,用于大规模图像分类和识别。NASNet架构特点是由两个AutoML设计的Layer组成——Normal Layer and Reduction Layer,这样的效果是不再需要相关专家用human knowledge来搭建卷积网络架构,直接用RNN把Hyperparameter计算出来,这样就实现了AI关于CNN网络结构的自动学习。 The controller RNN is a two-layer LSTM with 35 hidden units on each layer.It is trained with the ADAM optimizer (Kingma & Ba, 2015) with a learning rate of 0.0006. The weights of the controller are initialized uniformly between -0.08 and 0.08. For the distributed training, we set the number of parameter server shards S to 20, the number of controller replicas K to 100 and the number of child replicas m to8, which means there are 800 networks being trained on 800 GPUs concurrently at any time. 谷歌大脑提出的NAS上的Auto-regressive RNN 该模式具有如下优点: 首先,这是一个灵活的框架(可应用于自动化设计神经网络架构、神经优化器、设备配置、数据增强策略等)。 其次,这种方法在CIFAR和ImageNet等基准数据集上取得了当时最佳的结果。 缺点: 首先,这一模式通常依赖于大量的计算资源来取得好的结果(例如,NASNet使用了48000 GPU-hours)。 其次,遵循这一模式的许多方法仍然无法击败人工设计的最佳架构,尤其在计算资源受限的情况下。 既然我们已经有许多成功的人工设计的架构,现有的神经架构搜索方法都无法轻易超越它们,那么为什么不利用它们呢?这就相当于给网络搜索结构一个好的初始结构。 为了实现这点,上交大团队在AAAI 2018大会上发表的工作EAS(“Efficient Architecture Search by Network Transformation”)中提出:可以不从头开始进行神经架构搜索,而是使用现有的网络作为起点,通过网络变换(Network Transformation)的方式来探索架构空间。具体的,他们使用了Net2Net操作(一类 function-preserving的网络变换操作)来探索架构空间。 在之后的ICLR 2018上,来自CMU的研究人员提出了“N2N Learning: Network to Network Compression via Policy Gradient Reinforcement Learning”,即利用网络压缩操作来自动化地压缩一个训练好的网络。 局限性 Net2Net和网络压缩操作的局限性在于他们都是layer-level的操作,例如添加(修剪)过滤器和插入(删除)层。通过应用这些layer-level的操作仅能改变网络的深度和宽度,而不能修改网络的拓扑结构。这意味着在给定一个链式结构的起点时,它们总是会导致链式结构网络。 上海交大APEX数据与知识管理实验室和MIT韩松老师在今年ICML 2018上发表的新研究“Path-Level Network Transformation for Efficient Architecture Search”表明,利用现有的成功的人工设计的架构来设计高效的网络架构会容易得多。通过将现有成功的人工设计的架构与神经架构搜索方法在设计有效的路径拓扑方面的强大能力相结合,可以在有限的计算资源下获得更好的结果。 .................. 翻译文章:算力节省240倍,http://www.sohu.com/a/242769393_473283 考虑到当前最先进的人工设计的架构(例如Inception模型、ResNets和DenseNets等)已经超越了简单的链式结构布局,并且显示出精心定制的路径拓扑(path topology)的好处,因此对于这些基于变换的方法来说,这将是一个关键的需要解决的问题。 上交大和MIT的研究人员在ICML 2018发表的“Path-Level Network Transformation for Efficient Architecture Search”的主要目的便是解决这个问题。 .......... 改进方法: 解决方案是从一些简单的观察开始。考虑一个卷积层,如果我们把多分支结构( multi-branch structure)中的每一个分支都设为该层的复制,那么给定相同的输入,每个分支必然会产生相同的输出,这些输出的平均值也等于卷积层的输出。 因此,我们可以构造一个等效的多分支结构(multi-branch structure),并通过add操作合并卷积层。类似地,为了构造一个通过串联合并的等效多分支结构,可以将卷积层沿着输出通道维度分割为几个部分,并将每个部分分配给相应的分支。这样,它们输出的串联就等于卷积层的输出。 对于其他类型的层,例如 identity 层和深度可分离卷积层(depth-wise separable convolution layer,),可以类似地进行这种等价的替换。 identity层和等价的multi-branch结构 更进一步,通过将这些等价替换与Net2Net操作相结合,就可以任意修改神经网络的路径拓扑。 树形结构的架构空间 在路径级网络变换的基础上,研究人员探索了一个树形的结构空间(即多分支结构的一个简单的扩展)。 形式上,树形结构单元由节点和边组成。在每个节点,定义有一个分配方案,用于确定如何为每个分支分配输入特性映射(feature map);还有一个合并方案,用于确定如何合并分支的输出。节点通过边(edge)连接到每个子节点,而边被定义为一个单元操作(例如卷积、池化、 identity等)。 给定输入特性映射x,节点的输出将基于其子节点的输出递归地定义。首先将输入特性映射分配给每个分支。然后在每个分支上,分配的特征映射由相应的边和子节点处理。最后,合并它们以产生输出。 为了探索树形结构空间,研究人员使用了一个强化学习元控制器。这里的策略网络包括一个编码器网络,用于将输入架构编码成一个低维向量,以及各种softmax分类器,用于生成相应的网络变换操作。 此外,由于输入架构现在具有树形结构,无法简单用一个字符串序列来表示,因此这里使用了树形结构编码器网络( tree-structured encoder network)。 树形结构的编码器网络 具体来说,除了用于在边上执行隐藏状态变换的普通LSTM单元之外,还引入了两个额外的树结构LSTM单元,以在节点上执行隐藏状态转换。如上图所示,使用这3个LSTM单元,整个过程以自下而上和自上而下的方式进行,使每个节点中的隐藏状态包含架构的所有信息,类似于双向LSTM。 然后,给定每个节点的隐藏状态,做出三种不同类型的决策。第一种类型是确定是否要将一个节点转换为多个子节点。合并方案和分支数量都是预测的。第二种类型是确定是否插入新节点。第三种类型是用从一组可能的原始操作中选择的层来替换 identity 映射。 实验和结果 以下是论文中提供的受限的计算资源下(大约200 GPU-hours)找到的最好的树形单元(TreeCell-A): 我们可以将这样的树形单元嵌入到已有的人类设计的网络架构(例如DenseNet,PyramidNet)当中,而在CIFAR-10上的结果如下表所示 与原始的DenseNet和PyramidNet相比,树形单元显著提高了参数效率和测试误差结果。与其他从头开始的神经架构搜索方法(NASNet),TreeCell-A可以在大约一半参数的情况下实现更低的测试错误率(2.30% test error with 14.3M parameters versus 2.40% test error with 27.6M parameters)。更重要的是,其所使用的计算资源要比NASNet少得多。 当迁移到ImageNet(移动设置)时,与NASNets相比,树形单元仍然可以获得稍好的结果。 论文地址:https://arxiv.org/pdf/1806.02639.pdf 时序分析是一种变长模式分析,而语言翻译工作是sequence 2 sequence learning 工作。 对于空间内的手势识别算法,在线流程是这样的。不断输入的静态图像帧,从图像中获取手部,并实时检测出手的位姿。以位姿特征序列作为输入,模型的另一侧输入一个输出模式的概率。 文章:RNN的四种代表性扩展-. 作者:CHRIS OLAH Google Brain SHAN CARTER Google Brain Recurrent neural networks are one of the staples of deep learning, allowing neural networks to work with sequences of data like text, audio and video. They can be used to boil a sequence down into a high-level understanding, to annotate sequences, and even to generate new sequences from scratch!(RNN是深度学习的一种,广泛用于文本,语音和视频中。RNN可以将一个序列抽象到一个高维理解,做注释甚至可以生成一个新的序列) Four directions stand out as particularly exciting:(四个具有代表性的RNN扩展) Individually, these techniques are all potent extensions of RNNs, but the really striking thing is that they can be combined together, and seem to just be points in a broader space. Further, they all rely on the same underlying trick – something called attention – to work. Connectionist Temporal Classification (CTC)是一项技术,它是位RNN专门设计的顶层(top layer)。使得针对输入序列的每一帧,网络能够输出一个标签或者空白(blank)。CTC使得用一个RNN构建语音识别系统成为可能,这个和混合方法HMM+DNN不一样。文章:CTC方法详解补充 使RNN支持CTC模型所需要的输出表示,关键步骤是将网络输出转换为一个在label序列上的条件概率分布,之后对于给定输入,网络通过选择最可能的label来完成分类。 ............................ CTC原文翻译 因为最近做了一些用连续标签做文字识别标签任务的工作,对 ctc 有了一些了解,在此记录一下。 在学习 CTC 的时候,也看了不少博客,但是我觉得讲的最好的还是原论文 Connectionist Temporal Classification: Labelling Unsegmented Sequence Data with Recurrent Neural Networks 解释的最清楚。 文章:Connectionist Temporal Classification原文翻译 ……………………………. CTC 解决了对输入序列的单个词的切分和对输入序列的整合工作。 CTC 的优点 为解决RNN展开式的指数级参数传递的消失或爆炸问题,发明了LSTM网络。 RNN无疑是深度学习的主要内容之一,增强型RNN大致可以分为四种,本文介绍第一种:神经图灵机。 简单的RNNs(vanilla version)是存在很多缺陷的,直到出现LSTM,增加了gates使得gradient vanishing不在成为问题。前几天还看到关于LSTM之父 Sepp Hochreiter and Jürgen Schmidhuber(尤其后者)如今并没有很大名气的讨论,大家有兴趣也可以了解一下。如今所有state-of-the-art的RNNs几乎都在使用LSTM。关于理解LSTM,推荐Olah's Blog。 在这基础之上出现了很多更加 powerful 的增强型RNNs,这些研究都是非常激动人心的。而这其中我们主要讨论以下4种: 本质上,它们都是RNNs的扩展,并且它们甚至可以组合在一起使用,这是由于注意力机制的使用将它们联系在了一起。Attention将是RNNs发展史上一个非常重要的里程碑。这四种模型都是非常酷的,但由于时间和篇幅关系,我们先从Neural Turing Machine开始,剩下的在后续文章中讨论。也算是为了弥补我之前没有那么成功的 NTM 分享经验。 神经图灵机 - Neural Turing Machines NTM(Graves, et al., 2014)在一个很高的层面上构建神经计算模型,作为图灵机的实现。核心思想是在RNNs的基础上augment记忆模块。张量是神经网络的语言,因此记忆模块就是一组张量,具体地,原文使用一组向量来表示。实际上,只要可以保持一致性,使用一个高斯分布表示一个记忆单元也是可以的。 这里A被称作 controller(图中是在处理序列数据,有个错误,最后应该是x3,y3), 可以是FNNs(feedforward neural networks),也可以是RNNs,但RNNs能实现更多操作,因为它是 Turing Complete 的。 NTM的整个工作过程: 里面有个卷积操作比较有意思,稍微有点tricky,大家可以去原文里看,叫circular convolution。 之所以我说NTM是具有里程碑式意义的,是因为这种读写能力允许NTM执行许多简单的算法,这是超越传统神经网络的。 例如,他们可以学习在存储器中存储长序列,然后在其上循环、重复它。 当他们这样做,我们可以看到其在哪些位置进行读写以更好地了解NTM在做什么。一定意义上,作为图灵机的实现,它具有实现目前计算机能使用的所以算法,并且它是可学习的。不过要实现这个目标还有很多工作要做。 ...........未完待续.......... ...........哥德尔完全性定理和哥德尔不完备性定理,以及不可能达到却要努力去达到的希尔伯特大厦.......... 参考: Neural Turing Machine include Taehoon Kim’s(TensorFlow), Shawn Tan’s (Theano), Fumin’s (Go), Kai Sheng Tai’s (Torch), Snip’s (Lasagne); Differentiable Neural Computer: Mostafa-Samir(TensorFlow) Code for the Neural GPU: TensorFlow Models repository; Memory Networks include Facebook’s (Torch/Matlab), YerevaNN’s (Theano), and Taehoon Kim’s (TensorFlow).
1. ||x|| ≥0;
2. ||ax||=|a|||x||;
3. ||x+y||≤||x||+||y||。
范数的集合⟶赋范空间+线性结构⟶线性赋范空间
距离的集合⟶ 度量空间+线性结构⟶线性度量空间
线性赋范空间+内积运算⟶内积空间;
这时的内积空间已经有了距离、长度、角度等,有限维的内积空间也就是我们熟悉的欧氏空间。
内积空间+完备性⟶希尔伯特空间
其中完备性的意思就是空间中的极限运算不能跑出该空间,如有理数空间中的2–√ 的小数表示,其极限随着小数位数的增加收敛到2(1/2),但2(1/2属于无理数,并不在有理数空间,故不满足完备性。一个通俗的理解是把学校理解为一个空间,你从学校内的宿舍中开始一直往外走,当走不动停下来时(极限收敛),发现已经走出学校了(超出空间),不在学校范围内了(不完备了)。希尔伯特就相当于地球,无论你怎么走,都还在地球内(飞出太空除外)。
赋范空间+完备性⟶巴拿赫空间
距离⟶范数⟶内积
向量空间+范数⟶ 赋范空间+线性结构⟶线性赋范空间+内积运算⟶内积空间+完备性⟶希尔伯特空间
内积空间+有限维⟶欧几里德空间
赋范空间+完备性⟶巴拿赫空间函数空间与泛函分析
作用:核,可以用来快速判断一个向量是否是线性方程组的解。而值域,可以用来快速判断,一个向量是否可以通过其他向量,通过该线性变换后得到。可积可微可学习
张量分析及其他
专家系统与强化学习
DNN结构搜索
NetWork In NetWork:
NasNet网络逐层搜索
基于网络变换
拓扑结构搜索
树形结构的强化学习元控制器(RL Meta-Controller)
RNN方法
Sequence 2 Sequence Learning
变长序列的模式识别
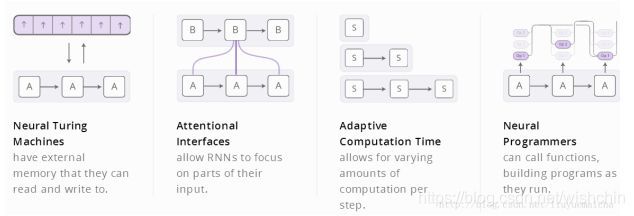
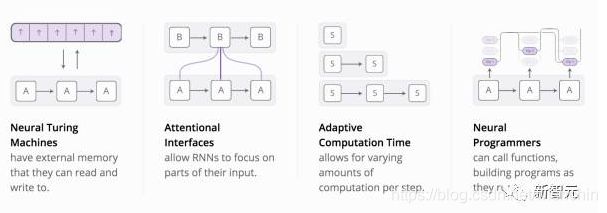
RNN的四种代表性扩展
原Paper:http://distill.pub/2016/augmented-rnns/#citation
Our guess is that these “augmented RNNs” will have an important role to play in extending deep learning’s capabilities over the coming years.
(个人认为,以上RNN技术的扩展都取得了显著的效果,更显著的是他们可以合并到一起,并且在更宽广的空间中取得更好的效果。进一步看,它们都依赖于相同的技巧——一种成为attention的东西——来工作。)
我们的猜测是这些扩展的RNN在今后的几年中将会扮演一个重要的角色。CCT方法
对于没接触过这个概念的人,可能加一些例子会更好理解一些。我就来加一些例子。
LSTM方法
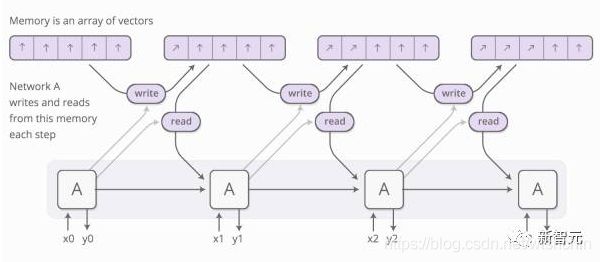
NTM方法