线段树入门与基础应用

线段树入门与基础应用

---

引入

线段树是一种二叉搜索树，与区间树相似， 它将一个区间划分成一些单元区间，每个单元区间对应线段树中的一个叶结点。 使用线段树可以快速的查找某一个节点在 若干条线段中出现的次数，时间复杂度为 O(logN)。而未优化的空间复杂度为2N， 实际应用时一般还要开4N的数组以免越界， 因此有时需要离散化让空间压缩。

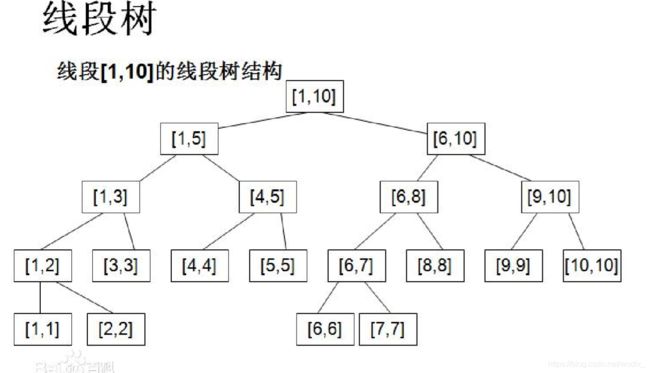
容易发现，根节点对应的是整个区间[1,10]。若一个节点对应的区间为[l,r]，当l=r是它是一个叶节点，没有左右儿子，否则它一定有左右儿子。左儿子对应的区间是[l,mid]，右儿子对应的区间是[mid,r]，mid=(l+r)/2。

---

基础应用

线段树维护每个区间上的最小值，实现如下几个函数。

1.初始建树

数组要开四倍大

const int N = 1e5 + 5;
int mi[N * 4];
void build(int k, int l, int r)//k为当前节点，l、r为当前区间
{
    if (l == r)
    {
        scanf("%d", &mi[k]);//叶子节点为原序列对应值
        return;
    }
    int mid = (l + r) / 2;
    build(2 * k, l, mid);//构建左树
    build(2 * k + 1, mid + 1, r);//构建右树
    mi[k] = min(mi[k * 2], mi[k * 2 + 1]);//自下往上更新
}

2.区间询问

int query(int k, int l, int r, int x, int y)//k为当前节点，l、r为当前区间，x、y为询问区间
{
    if (y < l || x > r)
        return INT_MAX; //若与询问区间无交集，返回一个极大值
    if (x <= l && r <= y)
        return mi[k]; //若询问区间包含当前区间，返回维护好的最小值
    int mid = (l + r) / 2;
    return min(query(2 * k, l, mid, x, y), query(2 * k + 1, mid + 1, r, x, y)); //否则分别处理左节点与右节点
}

3.单点修改

void change(int k, int l, int r, int x, int v) //x为要修改节点,v为要修改成的值
{
    if (r < x || l > x)
        return; //当前区间与原序列的位置完全没有交集
    if (l == r && l == x)
    {
        mi[k] = v;//修改相关叶子节点
        return;
    }
    int mid = (l + r) / 2;
    change(k * 2, l, mid, x, v);//左右区间进行修改
    change(k * 2 + 1, mid + 1, r, x, v);
    mi[k] = min(mi[k * 2], mi[k * 2 + 1]);//更新值
}

---

lazy标记

为进行区间修改，区间询问，我们引入lazy标记。考虑在每个节点上维护一个add，表示这个节点所对应的区间每个数都加上了add。区间修改时像之前区间询问那样，将区间拆成许多子区间，并且在线段树对应的节点上修改。
之前修改时没有选择将所有位置的值马上改变，而是将影响记录在根到叶子路径上的某节点处。询问时，则将影响加起来。

洛谷 P3372 【模板】线段树 1

#include 
using namespace std;
const int N = 1e5 + 5;
long long sum[4 * N];
int add[N * 4];
int n, m;
void build(int k, int l, int r)
{
    if (l == r)
    {
        cin >> sum[k];
        return;
    }
    int mid = (l + r) / 2;
    build(k * 2, l, mid);
    build(k * 2 + 1, mid + 1, r);
    sum[k] = sum[k * 2] + sum[k * 2 + 1];
}
void addsum(int k, int l, int r, int v)
{
    add[k] += v;
    sum[k] += (long long)v * (r - l + 1);//将影响累加起来
}
void pushdown(int k, int l, int r, int mid)//标记下传操作
{
    if (add[k] == 0)
        return;
    addsum(k * 2, l, mid, add[k]);//传到左节点
    addsum(k * 2 + 1, mid + 1, r, add[k]);//传到右节点
    add[k] = 0;//下传后清零
}
long long query(int k, int l, int r, int x, int y)
{
    if (y < l || x > r)
        return INT_MAX;
    if (x <= l && r <= y)
        return sum[k];
    int mid = (l + r) / 2;
    long long res = 0;
    pushdown(k, l, r, mid);
    if (x <= mid)
        res += query(k * 2, l, mid, x, y);
    if (mid < y)
        res += query(k * 2 + 1, mid + 1, r, x, y);
    return res;
}
void modify(int k, int l, int r, int x, int y, int v)
{
    if (l >= x && y >= r)
        return addsum(k, l, r, v);
    int mid = (l + r) / 2;
    pushdown(k, l, r, mid);//下传后更新
    if (x <= mid)
        modify(k * 2, l, mid, x, y, v);
    if (y > mid)
        modify(k * 2 + 1, mid + 1, r, x, y, v);
    sum[k] = sum[k * 2] + sum[k * 2 + 1];
}
int main()
{
    ios::sync_with_stdio(0);
    cin >> n >> m;
    build(1, 1, n);
    while (m--)
    {
        int t, x, y, k;
        cin >> t;
        if (t == 1)
        {
            cin >> x >> y >> k;
            modify(1, 1, n, x, y, k);
        }
        else
        {
            cin >> x >> y;
            cout << query(1, 1, n, x, y) << endl;
        }
    }
    return 0;
}