机器学习实战——支持向量机
机器学习实战——支持向量机
- 1 模型介绍
- 2 sklearn中的实现
1 模型介绍
假设给定一个样本集 D = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x m , y m ) } , y i ∈ { 1 , − 1 } D=\{(x_1,y_1),(x_2,y_2),...,(x_m,y_m)\},y_i\in\{1,-1\} D={(x1,y1),(x2,y2),...,(xm,ym)},yi∈{1,−1},在下图中,我们可以找到很多把样本划分为 { 1 , − 1 } \{1,-1\} {1,−1} 两类的超平面,但没办法判定哪一个是最好的。支持向量机的分类模型就是在样本集 D D D 中找到最合适的分离超平面,使模型具有较高的分类准确率。分离超平面可以用如下的公式表示:
![]()
则样本空间中任意一点到分离超平面的距离可以表示成如下形式:
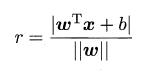
我们可以把分类问题转化为求点到直线的距离问题,距离超平面越远的点越容易被正确划分,可以进一步把问题转为求距离分离超平面最近的点的最大距离。
函数间隔:定义超平面 ( w , b ) (w,b) (w,b) 关于样本点 ( x i , y i ) (x_i,y_i) (xi,yi) 的函数间隔为 y i ( w T x i + b ) y_i(w^Tx_i+b) yi(wTxi+b) ,关于样本集的函数间隔为所有样本点的最小值,即:
r ^ = m i n { y i ( w T x i + b ) } \hat{r}=min\{y_i(w^Tx_i+b)\} r^=min{yi(wTxi+b)}
几何间隔:定义超平面 ( w , b ) (w,b) (w,b) 关于样本点 ( x i , y i ) (x_i,y_i) (xi,yi) 的几何间隔为 y i ∣ w T x i + b ∣ ∣ ∣ w ∣ ∣ y_i\frac{\mid w^Tx_i+b \mid}{\mid\mid w \mid\mid} yi∣∣w∣∣∣wTxi+b∣ ,关于样本集的几何间隔为所有样本点的最小值,即:
r = m i n { y i ∣ w T x i + b ∣ ∣ ∣ w ∣ ∣ } r=min\{y_i\frac{\mid w^Tx_i+b \mid}{\mid\mid w \mid\mid}\} r=min{yi∣∣w∣∣∣wTxi+b∣}
则函数间隔与几何间隔具有如下的关系
r = r ^ ∣ ∣ w ∣ ∣ r=\frac{\hat{r}}{\mid\mid w \mid\mid} r=∣∣w∣∣r^
上述求距离问题的目标函数可以表述成求几何距离的最大值,即:
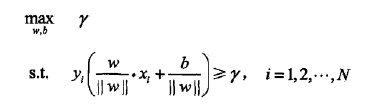
根据函数间隔与几何间隔的关系,上式可以转化成如下形式:
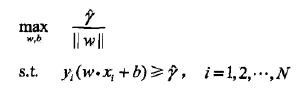
事实上函数间隔 r ^ \hat{r} r^ 对最优化问题无影响。假设将 w w w 和 b b b 按比例改变为 λ w \lambda w λw 和 λ b \lambda b λb ,则函数间隔变为 λ r ^ \lambda \hat{r} λr^ ,函数间隔的变化对上式最优化问题的约束条件与目标函数均无影响,即产生一个等价的最优化问题,与 r ^ \hat{r} r^ 的取值无关。为了研究的方便,可以取 r ^ = 1 \hat{r}=1 r^=1,则最优化问题转化为:
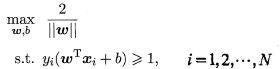
使约束条件等号成立的样本点被称为“支持向量”,其图形化的展示如下图: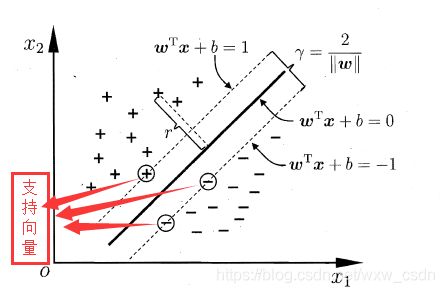
由于 1 ∣ ∣ w ∣ ∣ \frac{1}{\mid\mid w \mid\mid} ∣∣w∣∣1 的最大值等价于与 ∣ ∣ w ∣ ∣ 2 \mid \mid w \mid \mid^2 ∣∣w∣∣2 的最小值,因此,上式可以改写为:
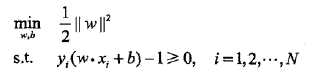
然后可以把上述问题转化为其对应的对偶问题进行求解,关于对偶问题的讲解可以参考这篇博文.
在引入松弛变量之后,上述问题转化成如下形式:
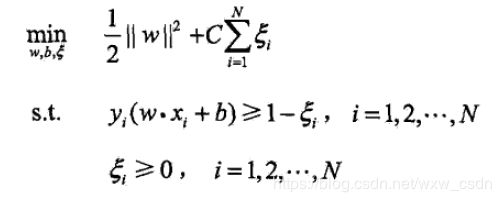
其对偶问题的形式如下:
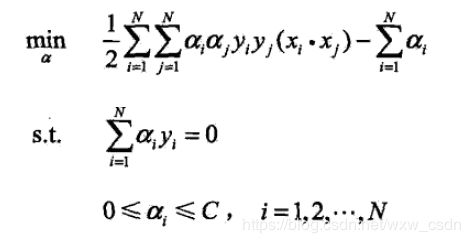
然后可以利用 SMO 算法进行求解,关于 SVM 及其 SMO 算法可以查看这篇文章。
关于 SMO 算法的思考:
SMO 算法中需要同时更新两个变量 α i 、 α j \alpha_i、\alpha_j αi、αj ,且
α i y i + α j y j = 常 数 \alpha_iy_i+\alpha_jy_j=常数 αiyi+αjyj=常数
在约束条件作用下,由于 y y y 的取值为 1 或者 -1,更新过程中 α \alpha α 需要满足的上下界可以表示成如下形式:
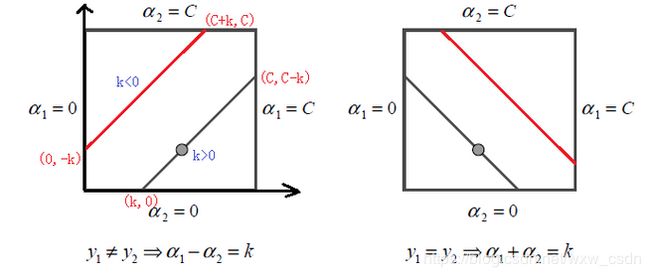
则其上下界可以表示成如下形式:
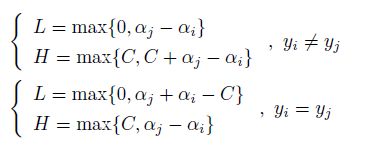
SMO 算法中每次更新 α i 、 α j \alpha_i、\alpha_j αi、αj 的启发式方法主要按照如下步骤:
1 先“扫描”所有乘子,把第一个违反 KKT 条件的作为更新对象,令为 α j \alpha_j αj;
2 在所有不违反 KKT 条件的乘子中,选择使 ∣ E i − E j ∣ \mid E_i − E_j\mid ∣Ei−Ej∣ 最大的 α i \alpha_i αi,并按照这篇文章的方法对 α i 、 α j \alpha_i、\alpha_j αi、αj 进行更新。
2 sklearn中的实现
sklearn 中支持向量机( SVM )的算法库分为两类,即分类算法库:SVC、NuSVC、LinearSVC,SVC 与 NuSVC 的区别仅仅在于对损失的度量方式不同,LinearSVC 是线性分类,不支持各种低维到高维的核函数,仅仅支持线性核函数,对线性不可分的数据不能使用。回归算法库:SVR、NuSVR、LinearSVR,SVR 与 NuSVR 的区别也仅仅在于对损失的度量方式不同。LinearSVR是线性回归,只能使用线性核函数。如果有经验知道数据是线性可以拟合的,那么使用 LinearSVC 去分类或者 LinearSVR 去回归,该算法不需要我们选择核函数以及调整对应参数,速度较快。如果对数据分布未知,一般使用 SVC 去分类或者 SVR 去回归,这就需要我们选择核函数以及对核函数调参。若对训练集训练的错误率或者说支持向量的百分比有要求,可以选择 NuSVC、NuSVR ,它们有一个参数来控制这个百分比。相关的类都包裹在sklearn.svm模块之中。详细的介绍可以参考官方文档。下面主要介绍 SVC 中的参数:
class sklearn.svm.SVC(C=1.0, kernel=’rbf’, degree=3, gamma=’auto_deprecated’, coef0=0.0, shrinking=True, probability=False, tol=0.001, cache_size=200, class_weight=None, verbose=False, max_iter=-1, decision_function_shape=’ovr’, random_state=None)
参数说明
C:错误项的惩罚参数,默认为 1.0
kernel:核函数,默认为高斯核 rbf,其他可选的有 linear、poly、sigmoid、precomputed 以及可调用自定义形式 callable。
degree:整数形,默认为 3。用于多项式核函数的度数 poly 。其他核函数忽略该参数。
gamma:浮点,默认为 auto ,即1/特征维度。该参数是 rbf、poly、sigmoid 的内核系数。
Coef0: 浮点型,默认为0.0。核函数的独立特征,仅仅在 poly 和 sigmoid 核函数中有意义。
probability:布尔型,可选,默认为 False 。是否启用概率估计,必须在调用fit之前启用,启用后会降低算法效率。
shrinking:布尔型,可选默认为True。是否使用缩减启发式。
Tot : 浮点型 默认为3.0。停止标准的公差
cache_size:浮点型,可选。指定内核缓存的大小(以MB为单位)。
Class_weight: 指定样本各类别的的权重,主要是为了防止训练集某些类别的样本过多,导致训练的决策过于偏向这些类别。这里可以自己指定各个样本的权重,或者用 balanced ,如果使用 balanced ,则算法会自己计算权重,样本量少的类别所对应的样本权重会高。当然,如果你的样本类别分布没有明显的偏倚,则可以不管这个参数,选择默认的 None。
verbose: 布尔型,默认为False。启用详细输出。 请注意,此设置利用libsvm中的每个进程运行时设置,如果启用,可能无法在多线程环境中正常工作。
max_iter:整型,可选默认 -1 。求解器中迭代的极限,或无限制的-1。
decision_function_shape:可以选择 ovo 或者 ovr ,0.19 版本默认是 ovr 。OvR (one ve rest) 的思想很简单,无论你是多少元分类,我们都可以看做二元分类。具体做法是,对于第 K 类的分类决策,我们把所有第 K 类的样本作为正例,除了第 K 类样本以外的所有样本都作为负例,然后在上面做二元分类,得到第 K 类的分类模型。其他类的分类模型获得以此类推。OvO (one-vs-one) 则是每次每次在所有的 T 类样本里面选择两类样本出来,不妨记为 T1 类和 T2 类,把所有的输出为 T1 和 T2 的样本放在一起,把 T1 作为正例,T2 作为负例,进行二元分类,得到模型参数。我们一共需要 T(T-1)/2 次分类。OvR 相对简单,但分类效果相对略差(这里指大多数样本分布情况,某些样本分布下 OvR 可能更好)。而 OvO 分类相对精确,但是分类速度没有 OvR 快。一般建议使用 OvO 以达到较好的分类效果。
SVC 算法与 sklearn 中其他算法的调用方法类似,本文以 iris 数据集为例进行说明:
from sklearn.svm import SVC
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
iris = load_iris()
iris_data = iris.data # 数据集
iris_labels = iris.target # 对应的分类标签
# 使用train_test_split对数据集按比例进行随机抽取,本文按37开进行抽取
X_train, X_test, Y_train, Y_test = train_test_split(iris_data, iris_labels, test_size=0.3, random_state=0)
# 定义分类器对象
svc = SVC() # 默认kernel='rbf'
# 调用所定义的分类器的训练方法,主要接收两个参数:训练数据集及训练标签
svc.fit(X_train,Y_train)
#调用该对象的测试方法,主要接收一个参数:测试数据集
Y_predict = svc.predict(X_test)
# 调用打分方法,计算模型在测试集上的准确率
score = svc.score(X_test,Y_test)